Файл: Вопрос Какие выводы можно сделать в случае, если построенная модель оказалась отвергнутой на этапе верификации.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 10.11.2023

Просмотров: 21

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Вопрос 7. Какие выводы можно сделать в случае, если построенная модель оказалась отвергнутой на этапе верификации?

Этап верификации предполагает проверку адекватности модели, т.е. проверку того, в какой степени построенная модель соответствует реальному экономическому явлению или процессу. Также, выясняется насколько удачно решены проблемы спецификации и параметризации, совершенствуется форма модели, уточняется состав объясняющих переменных, устанавливается точность расчетов по данной модели, общее качество уравнения, статистическая значимость найденных параметров.

Если построенная модель оказалась отвергнутой на этапе верификации, то следует вернуться к предыдущему этапу – этап параметризации. На этом этапе решается задача оценки значений параметров выбранной функции связи, т.е. задача подбора коэффициентов функции таким образом, чтобы эта функция в некотором смысле наилучшим образом отражала зависимость между объясняемым фактором и независимыми переменными. Следует пересмотреть подобранный коэффициент.
Вопрос 3. Дайте определение эконометрической модели. В чем отличие эконометрической модели от экономико-математической?

Эконометрическая модель – это форма представления взаимосвязи экономических показателей в виде суммы двух слагаемых, первое из которых отражает влияние на результативный признак выбранных факторов, а второе – влияние случайных величин.

Под экономико-математической моделью понимается экономическая модель, в которой структурные элементы и их взаимосвязи выражены в математической форме (т.е. в виде математической модели). Естественно, что под экономико-математическим моделированием понимают процесс построения, изучения и применения математических моделей в экономике.

Понятие экономико-математической модели шире, так как среди экономико-математических моделей особое место занимают эконометрические, балансовые и оптимизационные модели.

Эконометрические модели – это модели, в которых описываются корреляционно-регрессионные зависимости. Эти модели широко используются для построения производственных функций и прогнозирования экономических явлений.

Вариант 5. Задание:

По данным выборки (n =100) требуется:

1. Составить статистическое распределение выборки, предварительно записав дискретный вариационный ряд.

2. Составить интервальный ряд распределения относительных частот.

3. Построить гистограмму относительных частот.

4. Составить эмпирическую функцию распределения.

5. Построить график эмпирической функции распределения.

6. Найти основные числовые характеристики вариационного ряда:

• выборочное среднее

• выборочную дисперсию

• выборочное среднее квадратическое отклонение

• коэффициент вариации

7. Пояснить смысл полученных результатов.



Решение:

1. Отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда.

2.

xi
Кол-во, fi
xi·fi
Накопленная частота, S
|x-xср|·fi
(x-xср)2·fi
Относительная частота, fi/f

14
8
112
8
7.2
6.48
0.08

14.1
11
155.1
19
8.8
7.04
0.11

14.2
10
142
29
7
4.9
0.1

14.4
11
158.4
40
5.5
2.75
0.11

14.5
2
29
42
0.8
0.32
0.02

14.6
6
87.6
48
1.8
0.54
0.06

14.7
3
44.1
51
0.6
0.12
0.03

14.8
6
88.8
57
0.6
0.06
0.06

14.9
5
74.5
62
0
0
0.05

15
2
30
64
0.2
0.02
0.02

15.1
4
60.4
68
0.8
0.16
0.04

15.2
1
15.2
69
0.3
0.09
0.01

15.3
1
15.3
70
0.4
0.16
0.01

15.4
4
61.6
74
2
1
0.04

15.5
9
139.5
83
5.4
3.24
0.09

15.7
3
47.1
86
2.4
1.92
0.03

15.8
2
31.6
88
1.8
1.62
0.02

15.9
2
31.8
90
2
2
0.02

16
2
32
92
2.2
2.42
0.02

16.2
1
16.2
93
1.3
1.69
0.01

16.3
2
32.6
95
2.8
3.92
0.02

16.4
1
16.4
96
1.5
2.25
0.01

16.5
1
16.5
97
1.6
2.56
0.01

16.6
1
16.6
98
1.7
2.89
0.01

17.4
1
17.4
99
2.5
6.25
0.01

18.3
1
18.3
100
3.4
11.56
0.01

Итого
100
1490



64.6
65.96
1

3. Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.

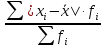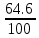???? = = = 0.646

Каждое значение ряда отличается от другого в среднем на 0.646

Дисперсия: ???? = 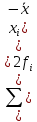= =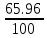 0.66

Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).

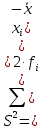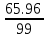= = 0.666

Среднее квадратическое отклонение.



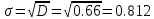
Каждое значение ряда отличается от среднего значения 14.9 в среднем на 0.812

Оценка среднеквадратического отклонения.



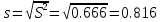
К. вариации:



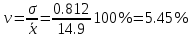
Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.


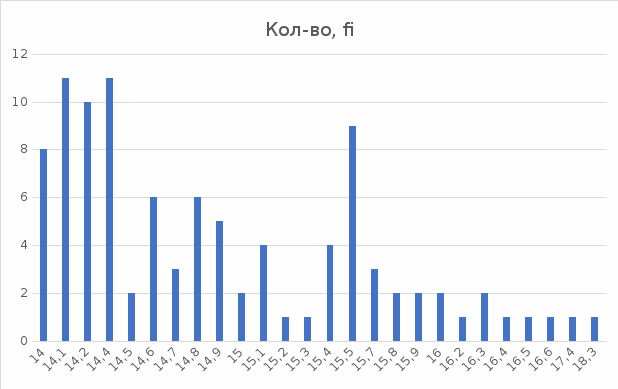
4. Интервальный ряд.

Число групп приближенно определяется по формуле Стэрджесса

n = 1 + 3,322log n = 1 + 3,322log(100) = 8

Ширина интервала составит:



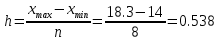
xmax - максимальное значение группировочного признака в совокупности.

xmin - минимальное значение группировочного признака.

Определим границы группы.

Номер группы
Нижняя граница
Верхняя граница

1
14
14.538

2
14.538
15.076

3
15.076
15.614

4
15.614
16.152

5
16.152
16.69

6
16.69
17.228

7
17.228
17.766

8
17.766
18.304

Группы
Середина интервала, xцентр
Кол-во, fi
xi·fi
Накопленная частота, S
|x-xср|·fi
(x-xср)2·fi
Относительная частота, fi/f

14 - 14.538
14.269
42
599.298
42
28.019
18.692
0.42

14.538 - 15.076
14.807
22
325.754
64
2.841
0.367
0.22

15.076 - 15.614
15.345
19
291.555
83
7.769
3.176
0.19

15.614 - 16.152
15.883
9
142.947
92
8.522
8.069
0.09

16.152 - 16.69
16.421
6
98.526
98
8.909
13.229
0.06

16.69 - 17.228
16.959



0
98
0
0
0

17.228 - 17.766
17.497
1
17.497
99
2.561
6.558
0.01

17.766 - 18.304
18.035
1
18.035
100
3.099
9.603
0.01

Итого



100
1493.612



61.719
59.695
1

Смотрите также файлы