КУРСОВОЙ ПРОЕКТТЕМА: ПОИСК ЭЙЛЕРОВОЙ ЦЕПИ ГРАФА Руководитель _________________________________________________________ подпись, датаИсполнитель студент ________________________________________________ подпись, датаТула 2023Содержание ВведениеДанная работа нацелена на проверку существования эйлерова цикла в графе.Эйлеров цикл - это эйлеров путь, являющийся циклом.Эйлеров путь (эйлерова цепь) в графе - это путь, проходящий по всем рёбрам графа и притом только по одному разу. Ясно, что эйлеров цикл содержит не только все ребра по одному разу, но и все вершины графа (возможно, по несколько раз). Очевидно также, что эйлеровым циклом может быть только связный граф.1 Постановка задачи курсового проектированияРазработка алгоритма и выполнение его программно для проверки существования эйлеровой цепи в графе. 2 Схема алгоритма Данный раздел содержит схемы алгоритмов. 2.1 Пошаговый алгоритм и его словесное описаниеСуть алгоритма, необходимого для решения задачи, в следующем. Пусть STACK – упорядоченное множество, которое будет содержать вершины графа, куда изначально помещается одна произвольная вершина. При каждой итерации вытаскиваем из STACK вершину и заносим в STACK все смежные с ней вершины, которые еще не занесены в массивaccess. Массив accessсодержит значения, которые указывают на достижимость i-той вершины графа. Повторяем эти действия до тех пор, пока STACKне пуст. Если все элементы accessистины, то следовательно можно добраться до каждой из вершин – граф связный. Далее проверяем количество ребер каждой вершины. Если у какой-либо вершины количество ребер нечетное, следовательно, по определению эйлерова цикла, он не существует, а если количество ребер четное, то эйлеров цикл существует.

---

1. Схема алгоритма
   

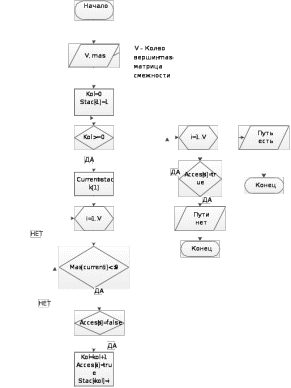
Пусть V – число вершин в графе, mas – массив, содержащий матрицу смежности графа, Stack – массив, содержащий вершины эйлерова цикла. Access – массив, содержащий значения, которые указывают на достижимость i-той вершины графа. Схема алгоритма представлена на рисунке 1.Рисунок 1 – Схема алгоритма 3 Описание структур данныхДанный раздел содержит описание основных структур данных, использованных в разработанном приложении. 3.1 Входные данныеV - количество вершин графа.mas - матрица смежности графа. 3.2 Выходные данныеПеременная типа bool.

2. Аспекты реализации на языке C#
   

Граф задается матрицей смежности. При реализации алгоритма были использованы: одномерные массивы (типа int и bool), переменные типа int, также используется Stack. Для ввода исходных данных используются: поле ввода NumericUpDown (для ввода количества вершин), таблица DataGridView (для ввода матрицы смежности). Полученные результаты выводятся на экран. Имеется возможность сохранять и открывать матрицу смежности в формате xml. Также предусмотрена функция случайного заполнения. Основные алгоритмы работы программы (программная реализация) приведена в приложении А. 5 Руководство пользователяДанный раздел создан для пользователя программы поиска эйлерова цикла в графе.Шаг 1. Вводим количество вершин в графе. Автоматически создается пустая матрица смежности. Шаг 2. Заполнить матрицу смежности (вручную или при помощи случайного заполнения). Шаг 3. Нажав кнопку «Проверить» выскакивает окно с ответом.6 Тестовые примеры Для тестирования алгоритма были созданы 2 графа.6.1 Тест первыйБыл создан граф с 4-мя вершинами. Эйлеров цикл в этом графе не существует. Матрица смежности и полученный результат на рисунке 2.

---

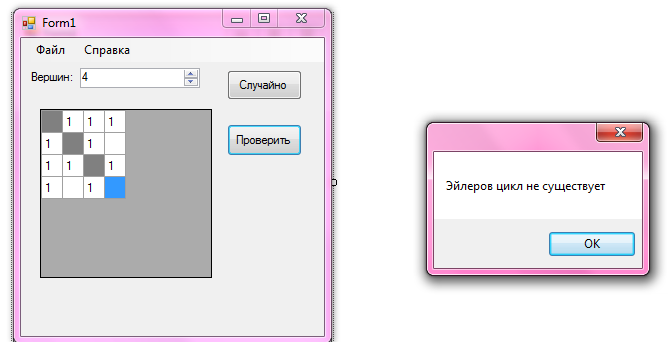
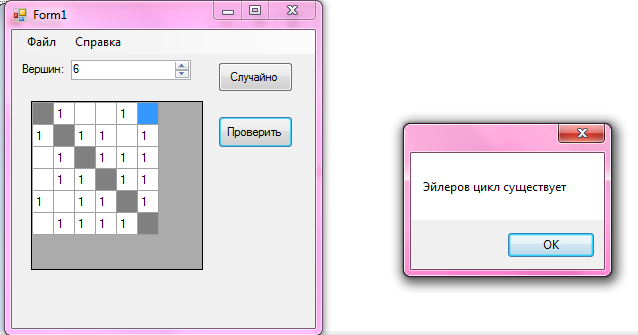
Рисунок 2 – Результат работы программы 6.2 Тест второйБыл создан граф с 6-ю вершинами. Эйлеров цикл в этом графе существует. Матрица смежности и полученный результат на рисунке 3.Рисунок 3– Результат работы программы ЗаключениеВ данной курсовой работе разработан алгоритм, позволяющий проверить существования эйлерова цикла в графе, и его программная реализация на языке C#. В результате тестирования была проверена правильность работы разработанного алгоритма и созданного приложения. Список использованных источников1. Эйлеров цикл [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/Эйлеров_цикл Приложение А(обязательное)private bool Way(){bool result = true;Stack dots = new Stack();

bool[] access = new bool[V];

access[0] = true;

dots.Push(0);

while (dots.Count > 0)

{

int current = dots.Pop();

for (int i = 0; i < V; i++)

{

if (mas[current, i] != 0 && access[i] == false)

{

dots.Push(i);

access[i] = true;

}

}

}

foreach (bool b in access)

if (b == false)

result = false;

return result;

}

private void button2_Click(object sender, EventArgs e)

{

mas = new double[V, V];

for (int i = 0; i < V; i++)

{

for (int j = 0; j < V; j++)

{

if (dataGridView1[j, i].Value != null)

mas[i, j] = Convert.ToInt32(dataGridView1[j, i].Value);

else

mas[i, j] = 0;

}

}

if (Way())

{

for (int i = 0; i < V; i++)

{

int kol = 0;

for (int j = 0; j < V; j++)

{

if (mas[i, j] != 0)

kol++;

}

if (kol % 2 != 0)

{

MessageBox.Show("Эйлеров цикл не существует");

return;

}

}

MessageBox.Show("Эйлеров цикл существует");

}

else

{

MessageBox.Show("Эйлеров цикл не существует");

}

}

---

Смотрите также файлы

• назначение и выплата пенсии за выслугу лет муниципальным служащим.docx

• .docx

• Химия факультеті Органикалы химия жне полимерлер кафедрасы ОУ (таныстыру) Тжірибе туралы есеп.docx

• Социальная перцепция.docx

• Занятие 3 Обучающийся Бобкова Алена Владимировна Преподаватель Данилова Елена Николаевна.doc