Файл: Решение. Каноническое уравнение эллипса имеет вид Для эллипса справедливо соотношение.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.11.2023
Просмотров: 20
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 1
Составить канонические уравнения: а) эллипса; б) гиперболы; в) параболы (
– точки, лежащие на кривой, 
– фокус, 
– большая (действительная) полуось, 
– малая (мнимая) полуось, 
- эксцентриситет, 
– уравнения асимптот гиперболы, 
– директриса кривой, 
– фокусное расстояние).а) эллипс,
Решение.
Каноническое уравнение эллипса имеет вид:
.Для эллипса справедливо соотношение:
. Из координат фокуса
, тогда получим:
.Полуоси найдены.
Напишем каноническое уравнение эллипса:
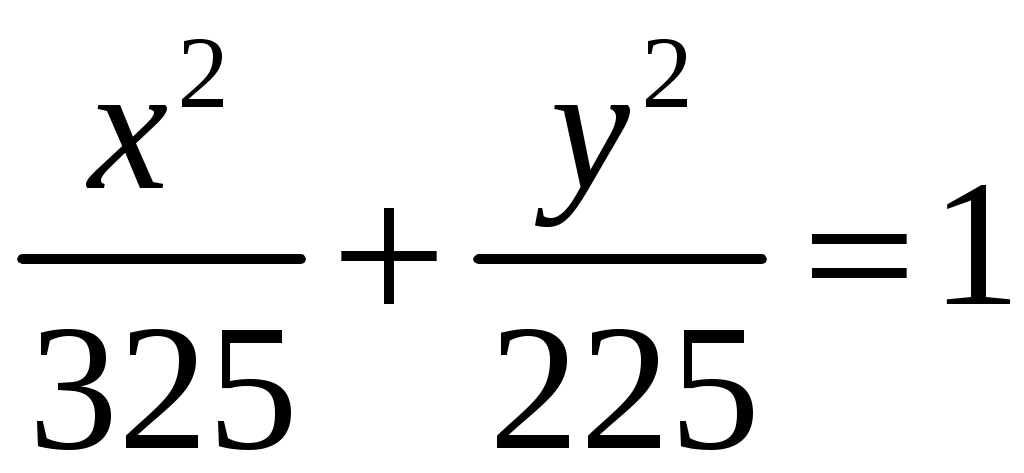.б) гипербола,
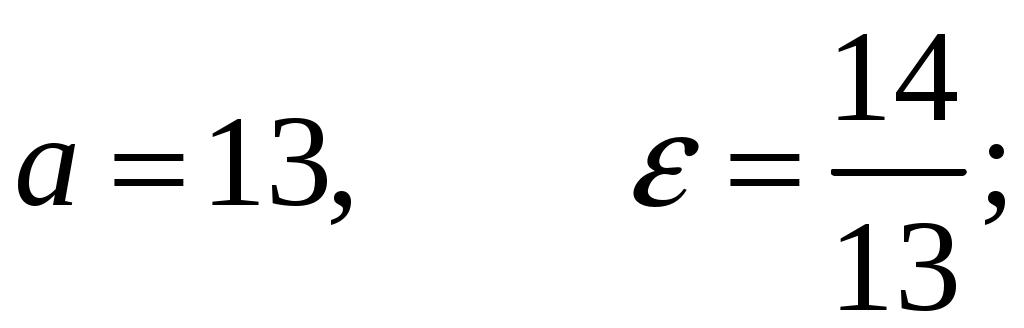
Решение.
Каноническое уравнение гиперболы имеет вид:
.Эксцентриситет гиперболы равен:
. По условию,
, тогда получим: 
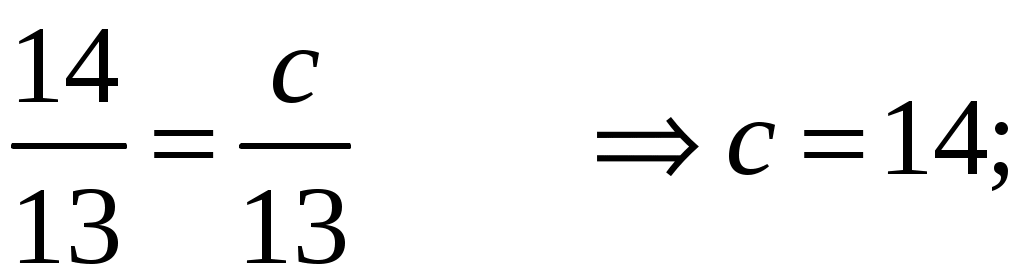
Для гиперболы справедливо соотношение:
, тогда получим:
Полуоси найдены.
Напишем каноническое уравнение гиперболы:
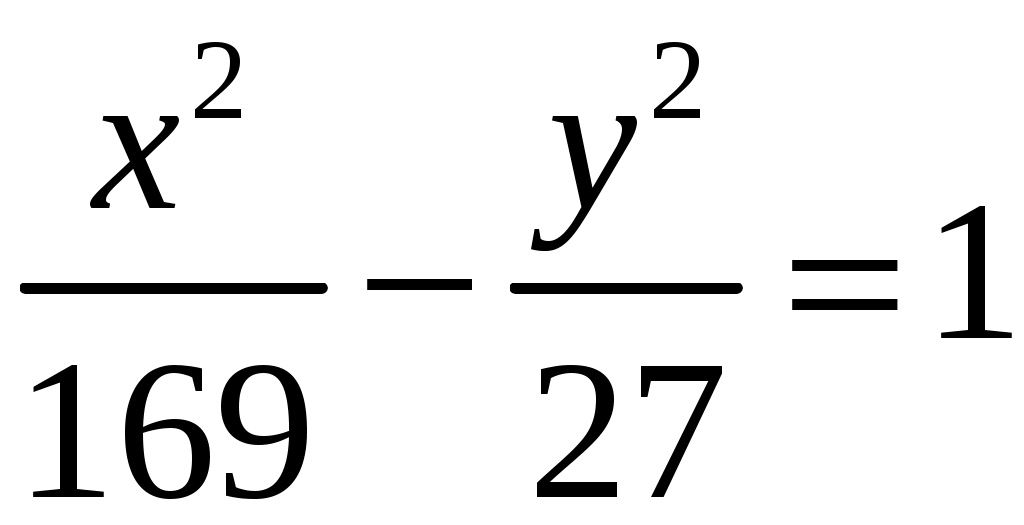.в) парабола, директриса
Решение.
Каноническое уравнение искомой параболы:
, где 
.Получим:
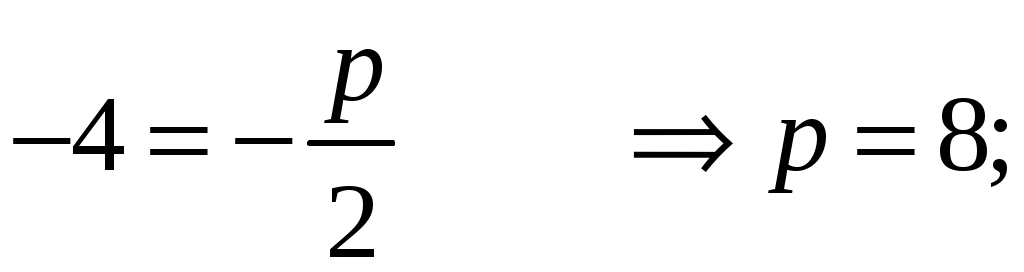
Напишем каноническое уравнение параболы:
.Задача 2.
Построить кривые, заданные следующими уравнениями.
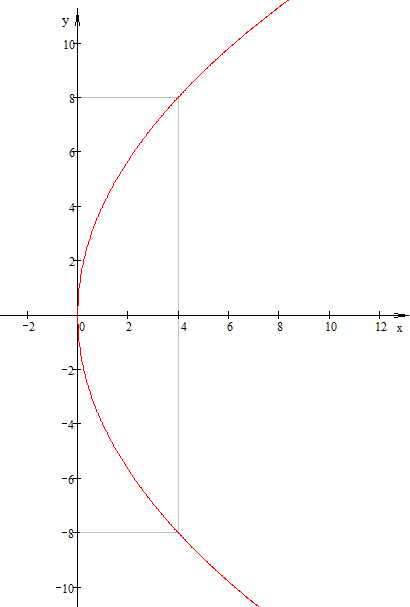
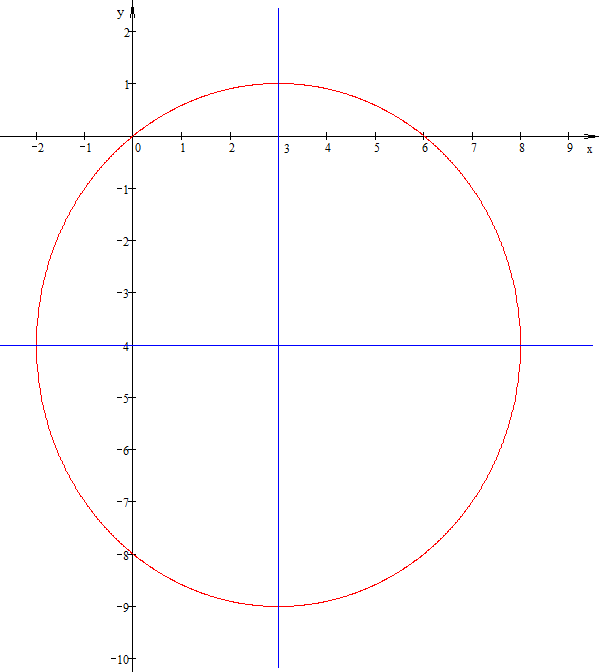
а)
Решение.
- окружность с центром в точке 
радиуса 
. Выполним чертеж.
б)
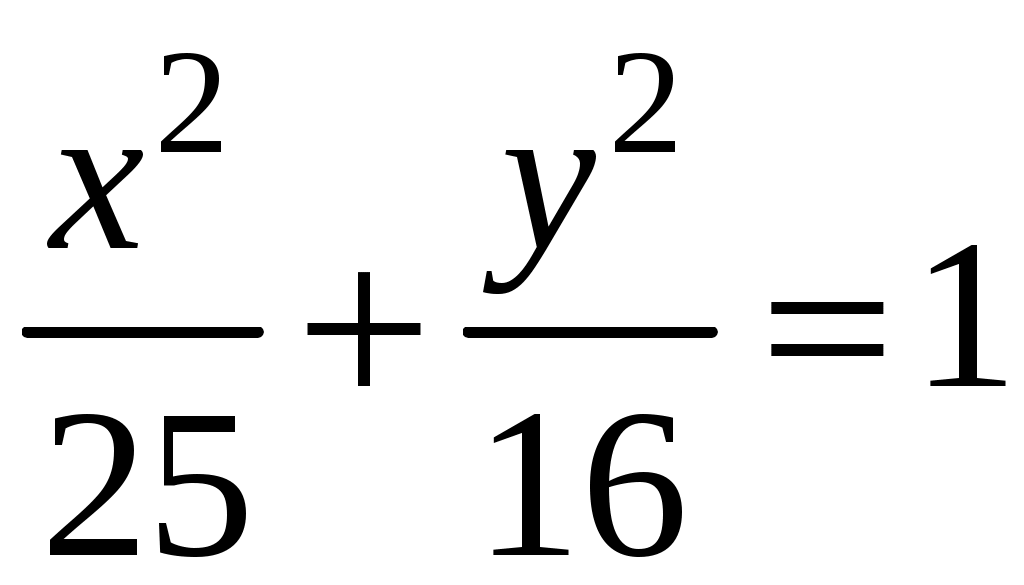
Решение.
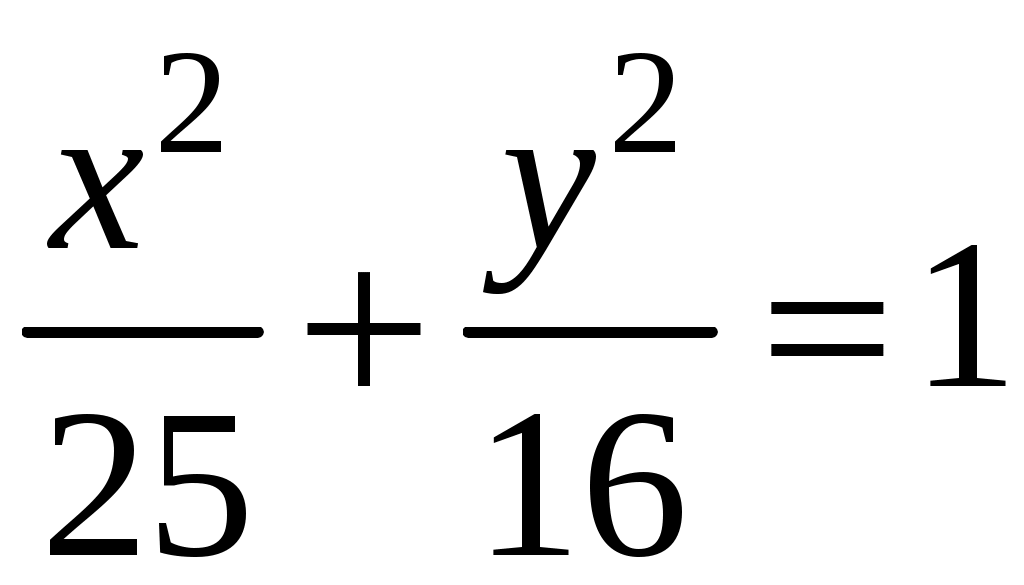- эллипс с центром в начале координат, 
- большая полуось, 
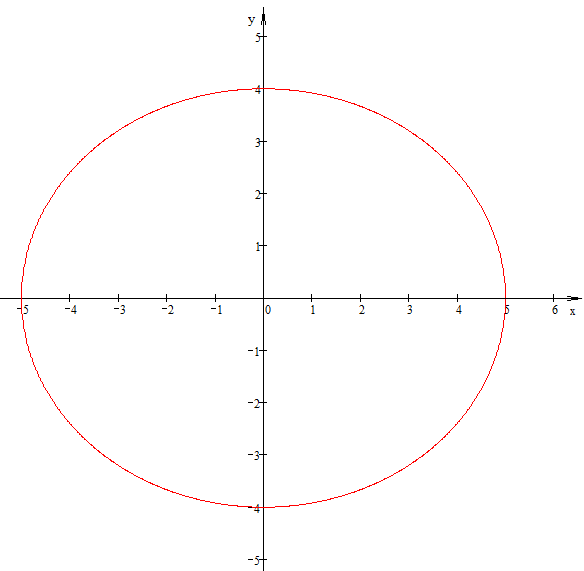
- малая полуось. Построим основной прямоугольник, откладывая от центра эллипса - точки
отрезки 
на осях 
и 
соответственно. Полученные вершины эллипса соединим плавной линией.
Выполним чертеж.
в)
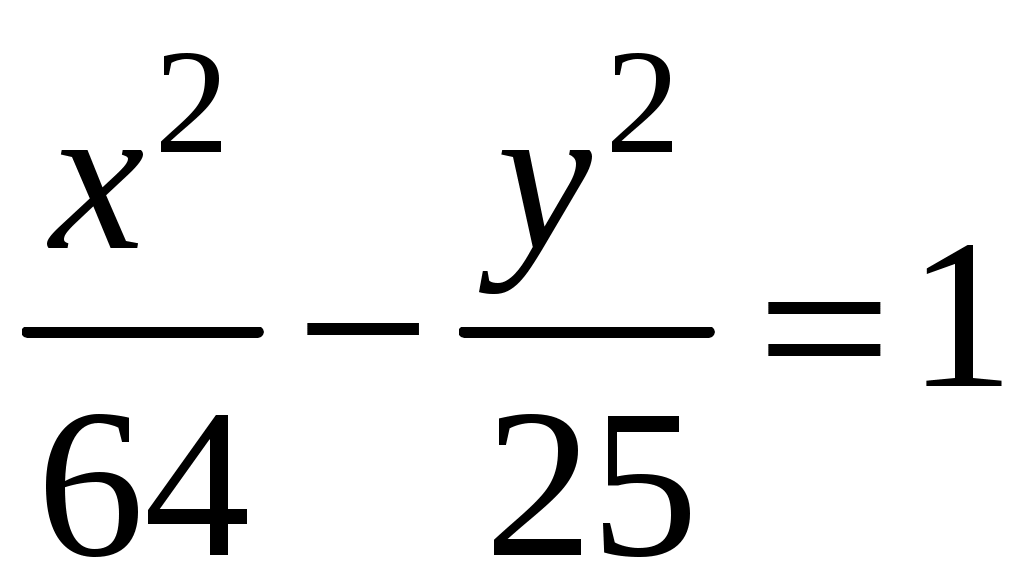
Решение.
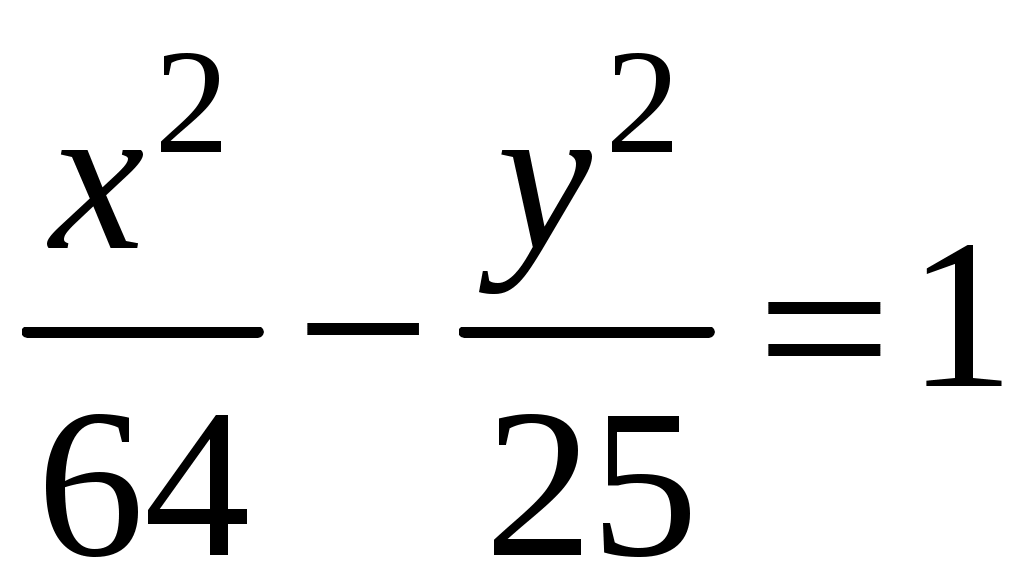- гипербола с вещественной осью 
, с центром в начале координат, 
- вещественная полуось, 
- мнимая полуось.Построим основной прямоугольник, откладывая от центра гиперболы - точки
отрезки 
на осях 
и 
соответственно. Диагонали прямоугольника будут являться асимптотами гиперболы. Выполним чертеж.
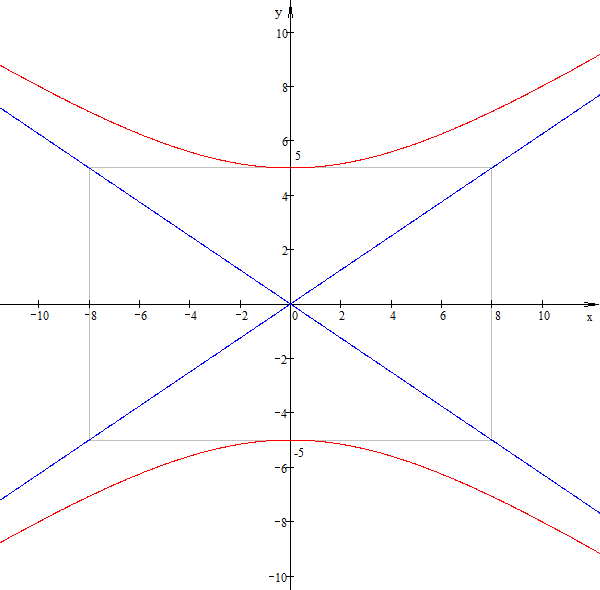
г)
Решение.
- парабола с вершиной в начале координат, 
- параметр, ветви направлены вправо.Характерные точки:
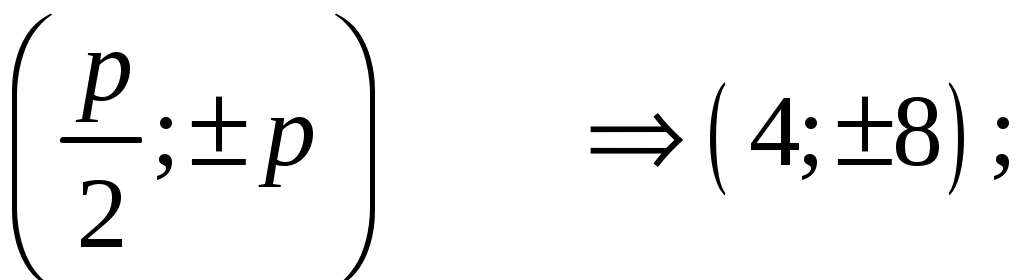
Выполним чертеж.
