Қазақстан республикасының білім және ғылым министрлігі

Қ.И. Сәтбаев атындағы Қазақ ұлттық техникалық зерттеу университеті



Ә. Бүркітбаев атындағы Өнеркәсіптік инженерия институты

Инженериялық физика кафедрасы

ЗЕРТХАНАЛЫҚ ЖҰМЫС №8
Клеман-Дезорм әдісімен ауа үшін адиабат

көрсеткішін анықтау

Зертханалық сабаққа арналған әдістемелік нұсқау


Алматы 2018
КЛЕМАН –ДЕЗОРМ ӘДІСІМЕН АУА ҮШІН

АДИАБАТ КӨРСЕТКІШІН АНЫҚТАУ
Жұмыстың мақсаты: Клеман-Дезорм әдісімен жылу сыйымдылықтарының қатынасын анықтау кезінде газдағы жүретін изопроцестерді зерттеу және ауа үшін 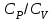қатынасын анықтау.

Керекті құрал-жабдықтар: шыны баллон, су манометрі, компрессор, секундомер.

1. ТЕОРИЯЛЫҚ КІРІСПЕ

1кг заттың температурасын 1К-ге қыздыру үшін қажетті жылу мөлшері 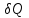меншікті жылу мөлшері c деп аталады:

.

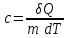Меншікті жылу сыйымдылықпен қоса молярлық жылу сыйымдылықты С қолданған ыңғайлы. 1 моль заттың температурасын 1К-ге қыздыру үшін қажетті жылу мөлшері молярлық жылу сыйымдылық С деп аталады:

, (1)

мұндағы 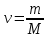– зат мөлшері, М– молярлық масса.

Меншікті с және молярлық жылу сыйымдылықтардың С арасындағы байланыс:

,

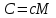орлардың өлшем бірліктері 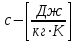және .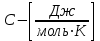

Егер заттың көлемі V немесе қысымы Р тұрақты болған процесте тұрақты көлем кезіндегі (

---

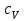
және 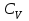) және тұрақты қысым кезіндегі ( 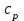және 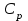) меншікті және молярлық жылу сыйымдылықтар болып ажыратылады.

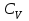және 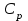-ларды термодинамиканың бірінші бастамасынан анықтаймыз. Жүйеге берілген жылу мөлшері Q жүйенің (газдың) ішкі энергиясын өзгертуге ΔU және газдың сыртқы күштерге қарсы атқарған жұмысына А жұмсалады: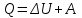



немесе дифференциалдық түрде былай жазылады:

. (2)

Жұмыстың формуласын ескеріп:

(3)

және жылу мөлшерін (1) өрнектен 1 моль газ үшін термодинамиканың бірінші заңын мына түрде жазуға болады:

CdT=dU_M+pdV . (4)

Изохоралық процесс кезінде ( 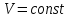) газдың атқаратын жұмысы нөлге тең (А=0). Ал сырттан газға берілген жылу,газдың ішкі энергиясын арттыруға (өзгертуге) жұмсалады. Демек, массасы m газдың температурасын арттырған кезде оның ішкі энергиясы келесі шамаға артады:
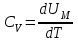. (5)

Осыдан, массасы m газдың температурасын арттырған кезде, оның ішкі энергиясы келесі шамаға артады:

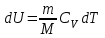. (6)

Егер газ изобаралық ( ) қызатын болса, онда (4) өрнекті мына түрде жазуға болады: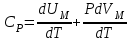

,

мұндағы 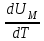процесс түріне тәуелді болмайды (идеал газдың ішкі энергиясы қысымға да Р көлемге де V тәуелді емес, тек температурамен анықталады) және ол әрқашан 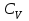-ға тең. Тұрақты қысымда ( 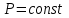) 1 моль газ теңдеуін 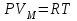дифференциалдасақ, онда универсал газ тұрақтысын аламыз, яғни:

---

.

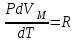Нәтижеде: 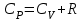. (7)

Бұл өрнек (7) Майер теңдеуі деп аталады. C_P әрқашан да 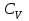-дан универсал газ тұрақтысына R артық.

C_P және 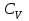жылу сыйымдылықтарын молекуланың дәрежелер саны і арқылы өрнектеуге болады (молекуланың кеңістіктегі орнын толық анықтайтын тәуелсіз шамалар саны). Оны молекуланың «еркіндік дәрежесі» деп те атайды.

1 моль идеал газдың ішкі энергиясы 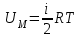болса, онда:

, .

Термодинамикалық процесстерді қарастырған кезде әрбір газ үшін қатынасын арқылы белгілеу маңызды сипатқа ие:

. (8)

Молекулалардың еркіндік дәрежесі і деп, молекулалардың кеңістікте орынын анықтайтын тәуелсіз координаттар санын немесе молекулалардың кеңістікте қозғала алу мүмкіндіктер санын айтады: біратомды молекула үшін і=3; екіатомды молекула үшін і=5; үшатомды және көпатомды молекулалар үшін і=6.

Адиабаталық процесс теңдеуіне кіретін шамасы адиабаттық көрсеткіш деп аталады. Ол жүйе мен сыртқы орта арасында жылу алмасу болмайтындығымен (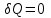 ) сипатталады. Бірінші жуықтауда тез жүретін процестерді адиабаталық деп есептеуге болады.

Адиабаталық процесс үшін термодинамиканың бірінші бастамасынан (2):

,

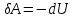яғни сыртқы күштердің жасайтын жұмысы жүйенің ішкі энергиясының өзгеруі есебінен жүреді. Бұл теңдеуден (3) және (6) өрнектерін ескере отырып, мына өрнекті аламыз:

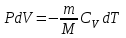. (9)

Бұдан, газ көлемінің өзгеруі оның температурасының өзгеруімен қатар өзгеріп отырады. Минус таңбасы адиабаталық ұлғаю кезінде (dV>0) газдың салқындауын (dT

---

<0), ал адиабаталық сығылу кезінде (dV<0) қызуын (dT>0)көрсетеді.

Идеал газ күйінің негізгі теңдеуін дифференциалдап, мына теңдеуді аламыз: .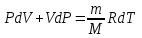

Алынған теңдеуді (9) өрнекке бөліп және (7) және (8) өрнектерді ескеріп келесі өрнекті аламыз: .

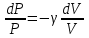Бұл теңдеудің екі жағын P₁-ден P₂ дейін және V₁-ден V₂ дейін интегралдап төмендегі теңдеуге келеміз:

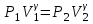. (10)

1 және 2 еркін таңдап алынған күйлер, сондықтан жалпы жағдайдағы адиабаталық процесті мына түрде жазуға болады:

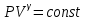. (11)

Бұл теңдеуді (11) Пуассон теңдеуі деп атайды. Изотермиялық процесс теңдеуі:

PV = const.

(11) теңдеудегі адиабаталық көрсеткішті Клеман-Дезорм әдісімен тәжірибе жүзінде анықтауға болады.
2. ТӘЖІРИБЕЛІК ҚОНДЫРҒЫНЫҢ СИПАТТАМАСЫ

Өлшеу үлкен шыны баллоннан Б, компрессордан Н және су манометрден М тұратын қондырғыда (1 сур.) жасалады. Баллон К краны арқылы компрессормен, К₀ краны арқылы атмосферамен жалғанған.

Ұсынылған Клеман-Дезорм әдісі (1819ж.) бір күйден екінші күйге өтетін екі тізбектелген процестермен, яғни адиабаталық және изохоралық процестермен жүретін газдың параметрлерін зерттеуге негізделген. Бұл процестер P-V диаграммасында 1-2 және 2-3 қисықтарына сәйкес ұсынылған. Егер баллонға ауаны толтырып және сыртқы ортамен жылулық тепе-теңдік орнағанша ұстасақ, онда алғашқы күйде газ P₁, V₁,T₁ параметрлеріне ие болады. Бұл кезде баллондағы газдың температурасы сыртқы ортаның температурасына тең, ал қысымы Р₁=Р₀+Ратмосфералық қысымнан кішкене үлкен болады. K₀ кранды ашқан кезде баллондағы ауа 2-ші күйге өтеді. Оның қысымы атмосфералық қысымға дейін P₂=P₀ төмендейді. Ауаның 1 күйдегі қалған массасы баллонның бір бөлік көлеміне ұлғая отырып, барлық V₂ көлемді алады.

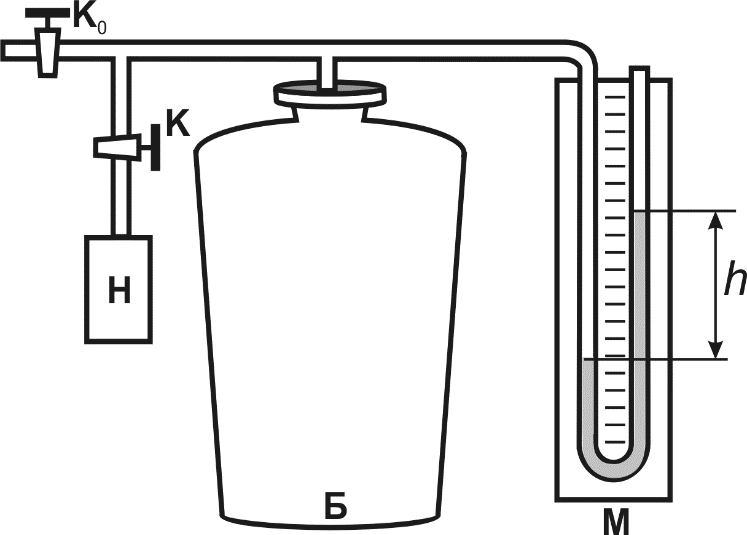1 сурет.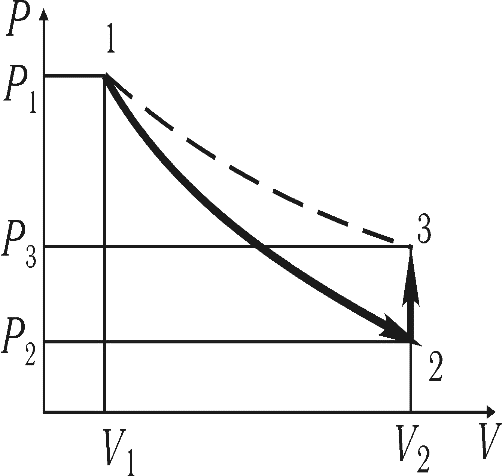

2 сурет.

---

Бұл кезде баллонда қалған ауа температурасы төмендейді. Газдың тез ұлғаюы кезінде газдың баллон қабырғасы арқылы сыртқы ортамен жылу алмасуды ескермеуге болады. Онда 1-2 процесті адиабаталық деп есептейміз:

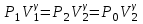. (12)

К₀ кранды жапқаннан кейін баллондағы адиабаталық ұлғайған салқын ауа тұрақты көлем V₂=V₃кезде (2 сур.) сыртқы ортаның температурасына T₃=T₁ дейін (2-3 процесс аралығында) қызады. Бұл кезде баллондағы қысым Р₃=Р₂+Р дейін артады.

Ауаның артық қысымдары Р' және Р'' U -формалы манометрдегі тығыздығы  сұйықтың деңгейлерінің айырымы бойынша өлшенеді:

Р' = gH; P'' = gh, (13)

мұндағы H және h -1 және 3 күйлерге сәйкес манометрдің көрсетуі.

Онда:

.

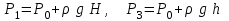Ауаның 1 және 3 күйлері изотермиялық процеске сәйкес келеді, сондықтан:

P₁V₁ = P₃V₃. (14)

(12) және (14) теңдеулерден көлемдердің қатынасын қысымдардың қатынасымен алмастырып, қысымдардың байланысын табамыз:



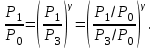
(13) өрнекті ескеріп Р₁ және Р₂ қысымдарды Р₀ арқылы өрнектеп және логарифмдейміз:



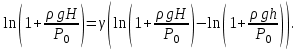
Егер х<<1 болса, онда мына математикалық қатынастан ln(1+х)=х, мұндағы x=ρgHсол жақтағы теңдеуге тең шама, ал оң жақтағы теңдеу үшін сәйкесінше x=ρghтең болады. Сонда:

.

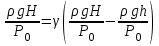Осыдан адиабаталық көрсеткіш γ есептейтін формуланы аламыз:

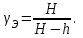(15)

Сонымен, ауа үшін жылу сыйымдылықтарының қатынасын анықтау үшін (1-2-3) процестерін алу қажет және газдың 1 және 3 күйлеріне сәйкес манометрдің Н және һ көрсетулерін өлшеу керек. Бірақ бірқалыпты адиабаттық процесті алу қиын: егер газдың тез ұлғаюын жүргізсек, онда процесс бірқалыпты болмайды, өйткені газдың температурасы мен қысымы көлем бойынша теңесіп үлгермейді. Баяу адиабаталық процесті жүргізу үшін баллонның жылулық изоляциясы қажет. Берілген қондырғыда t уақытта жылу шығарылумен газ ұлғаяды. Сондықтан соңғы изохоралық қызуда газдың қысымы аздап көтеріледі, яғни өлшенетін һ'< һ адиабат көсеткішін

---

Смотрите также файлы

• 1саба. Жас маман мраты жмыс табу таырып бойынша тапсырмалар рметті студенттер! Жас маман мраты жмыс табу.docx

• Узел законченая сборочная еденица состоящая из деталей общего функционального назначения. Механизмсистема деталей,предназначеная для передачии преобразования движения.docx

• Работа моу Хомутининская сош по патриотическому воспитанию 20222023 уч год.docx

• Статьи Совершенствование применения информационных технологий в правоохранительной деятельности.docx

• Министерство науки высшего образования российской федерации.doc