Файл: Пример.doc

4.1 Методика розв’язання системи диференціальних рівнянь математичної моделі за допомогою MatLAB

Розв’язання даної системи рівнянь було здійснено блоково аналітичним методом. Основна блок-схема розв’язання системи диференціальних рівнянь представлена на рис. 3.7. Вона складається з блоку 1, в якому записуються величини констант, що використовуються у основній системі, за допомогою блоків FROM та GOTO.

Блоки 2, 3, 4 – це підсистеми, в яких за допомогою математичних та логічних блоків записані рівняння перше, друге та третє рівняння системи (3.1) відповідно. Розгорнутий вид підсистем показаний на рис. 4.1, 4.2, 4.3.

Блок 6 є засобом візуалізації графічних залежностей вихідних величин, що отримуються в результаті розв’язання даної системи диференціальних рівнянь (рис. 3.1), блоки 5, що структурують значення вихідних величин у вигляді масиву координат точок та записують їх до відповідного поля – workspace.

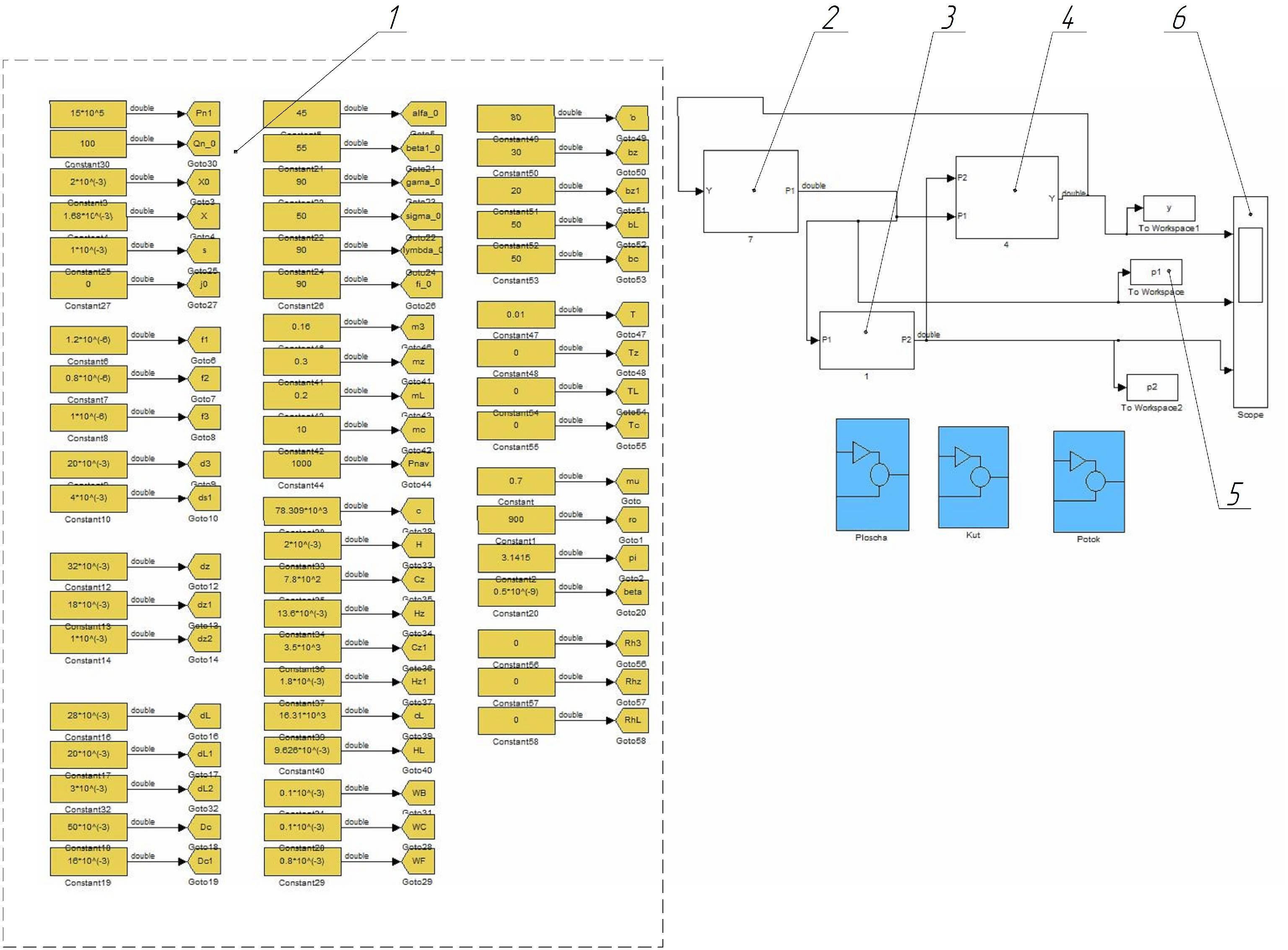
Рис. 4.1 – Основна блок-схема системи диференціальних рівнянь

Рис. 4.2 – Перше диференціальне рівняння системи (3.1) записане в логічно-блоковому вигляді

Рис. 4.3 – Друге диференціальне рівняння системи (3.1) записане в логічно-блоковому вигляді

Рис. 4.4 – Візуалізація розв’язку системи диференціальних рівнянь в графічному вигляді

У процесі дослідження гідросистеми застосовувався метод математичного моделювання. Розрахункова схема та математична модель, дозволяють дослідити вплив основних конструктивних параметрів на якісні характеристики гідросистеми. Для розв’язку диференціальних рівнянь використовувався пакет програм МatLAB Simulink. Вирішення даної системи рівнянь було здійснено комбінованим блоково-аналітичним методом.

Для покращення динамічних характеристик було проведено дослідження впливу конструктивних параметрів системи (кута нахилу кромки основного золотника – α, коефіцієнтів в’язкого демпфування основного золотника та золотника переливного клапана – b та b_Z відповідно) на коливальність, час перехідного процесу та перерегулювання.

На рис. 4.5 – 4.7 показано графіки залежностей динамічних характеристик від конструктивних параметрів системи.

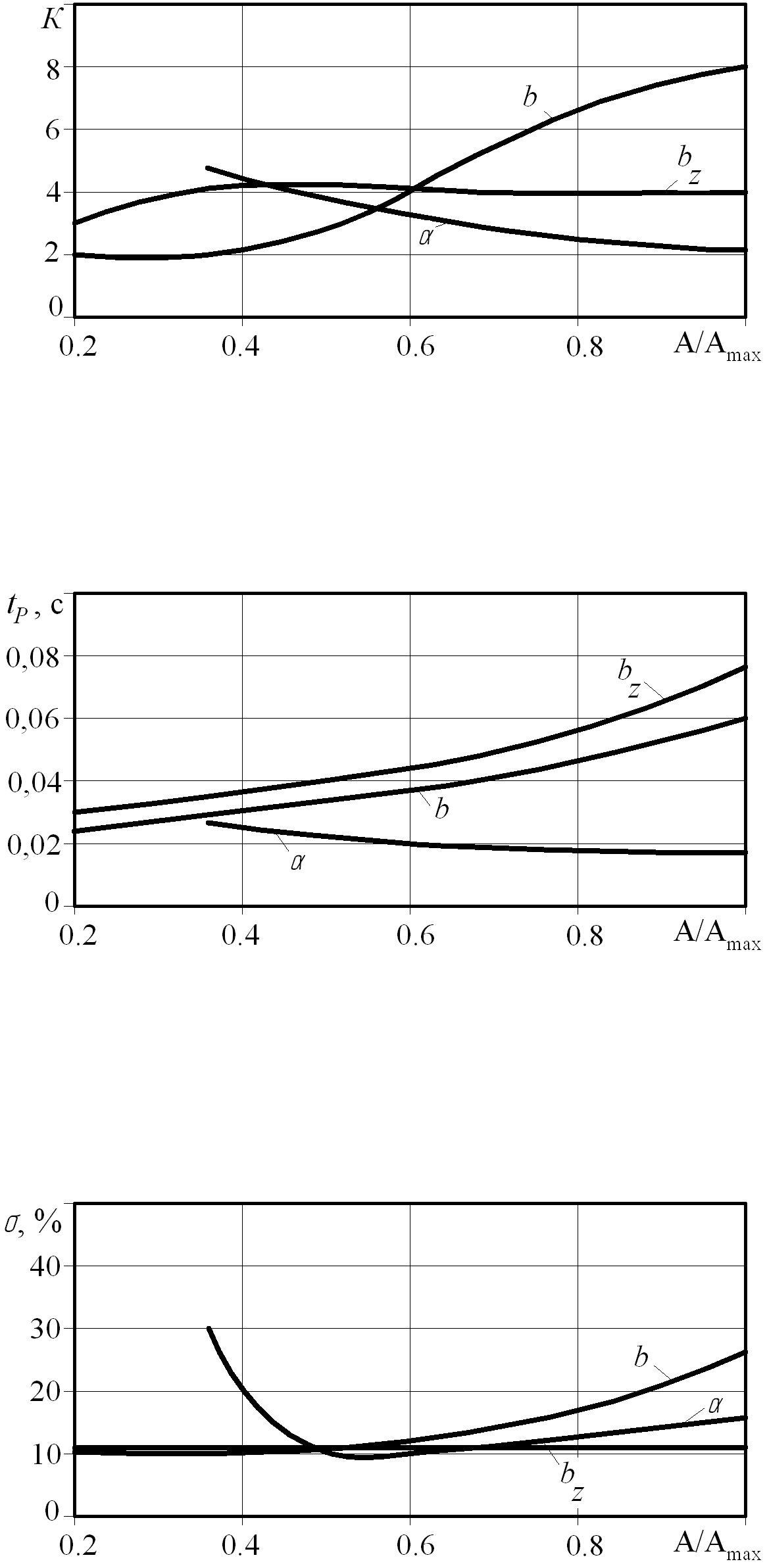
Рис. 4.5 –Залежність коливальності К від конструктивних параметрів системи b, b_z, α

Рис. 4.6 – Залежність часу перехідного процесу t_p від конструктивних параметрів системи b, b_z, α

Рис. 4.7 – Залежність перерегулювання σ від конструктивних параметрів системи b, b_z, α

Висновок: конструктивні параметри системи управління розподільником мають неоднозначний вплив на характеристики гідросистеми, вибір значень конструктивних параметрів системи управління розподільником ускладнений оскільки при їх зміні одні характеристики покращуються, а інші погіршуються.

Користуючись залежностями отриманими в ході роботи, можна знайти сполучення конструктивних параметрів, які забезпечують покращення динамічних характеристик системи, тобто отримання мінімальної коливальності, часу перехідного процесу та перерегулювання.