Файл: Лабораторная работа 1 по учебному курсу Физика 3.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 131

Скачиваний: 7

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»



Тольяттинский государственный университет

(наименование института полностью)

Техносферная безопасность

(Наименование учебного структурного подразделения)

Безопасность технологических процессов и производств

(код и наименование направления подготовки / специальности)



(направленность (профиль) / специализация)



Лабораторная работа №1
по учебному курсу « Физика 3» (наименование учебного курса)
Вариант __3__ (при наличии)


Обучающегося
В.А.Леонтьевой






(И.О. Фамилия)



Группа
ТБбп-1902б












Преподаватель

Ясников Игорь Станиславович





(И.О. Фамилия)




Тольятти 2023
Лабораторная работа

Опыт Юнга (вариант 3)

Цель работы: знакомство с моделированием процесса наложения когерентных электромагнитных волн, изучение закономерностей взаимодействия световых волн от двух источников (щелей) и экспериментальное определение расстояния от щелей до экрана.


Краткая теория

Интерференция света – это перераспределение светового потока в пространстве при наложении двух или нескольких когерентных волн с образованием максимумов и минимумов интенсивности света.

Когерентными называются волны, имеющие одинаковую частоту и постоянную разность фаз, не изменяющуюся с течением времени.

Волны, излучаемые реальными источниками света (исключение –лазеры), не являются когерентными. Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдают интерференционную картину.

Одним из методов наблюдения интерференции является метод Юнга рис.1.



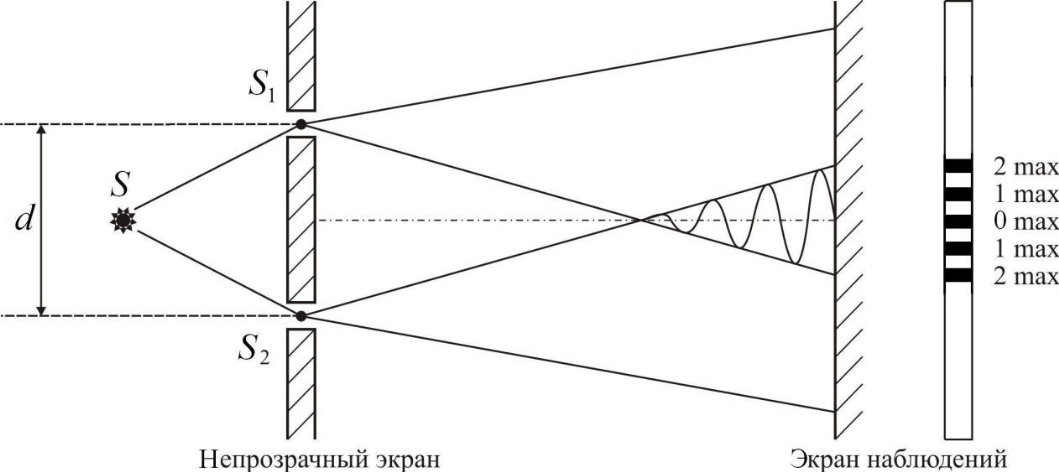
рис.1. Метод Юнга

Свет от некогерентного точечного источника света S попадает на непрозрачный экран с двумя узкими щелями, расположенными на расстоянии d (см. рис.1). Эти щели являются когерентными источниками S1 и S2. В пространстве происходит перекрытие световых пучков от этих источников. На экране наблюдений в зависимости от оптической разности хода волн наблюдается чередование максимумов и минимумов освещенности.

Максимум при интерференции волн наблюдается на экране при условии, что оптическая разность хода Δ волн, приходящих в некоторую точку А экрана, равна целому числу длин волн в вакууме или четному числу длин полуволн.

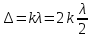(1)

где 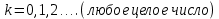; 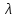- длина волны в вакууме.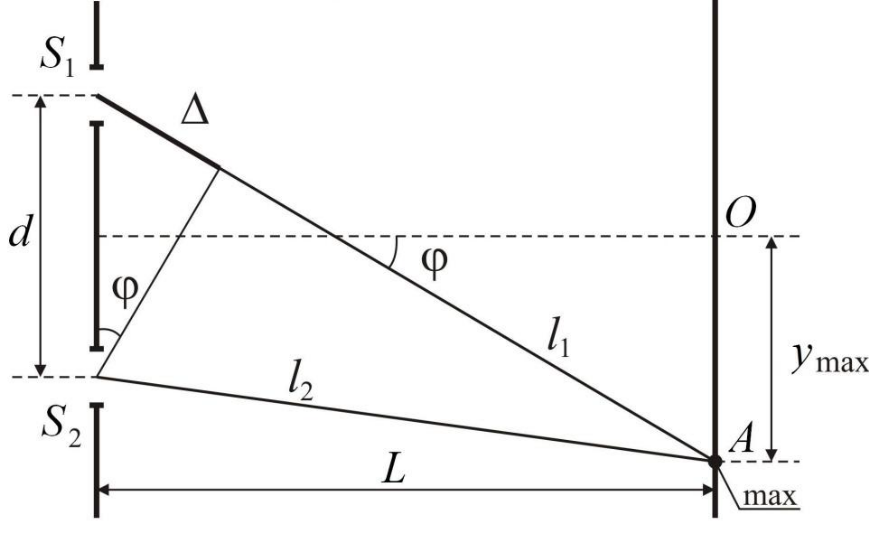



рис.2. К расчету интерференционной картины

Оптическая разность хода лучей от когерентных источников S1 и S2 равна разности геометрических путей l1 и l2, умноженной на абсолютный показатель n преломления среды (рис.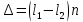2).

(2)

В опыте Юнга распространение световых волн происходит в воздухе и оптическая разность их хода равна геометрической, так как n = 1. Из рис.2 видно:
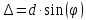
(3)

Так как расстояние от щелей до экрана 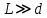, а угол 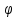мал, то

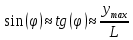(4)

где 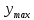- координата максимума, отсчитываемая от центра интерференционной картины. Тогда с учетом выражений (1) и (3) при

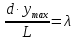(5)

Откуда

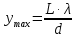(6)

Экспериментальная часть

  1. Выполним эксперимент на виртуальной установке рис.3. для вводных данных нашего варианта. Подведем маркер мыши к движку регулятора на картинке спектра. Нажмем левую кнопку мыши и, удерживая ее в нажатом состоянии, подвинем движок, установив цвет волны, соответствующий для нашей бригады. Установим так же нужное значение .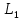



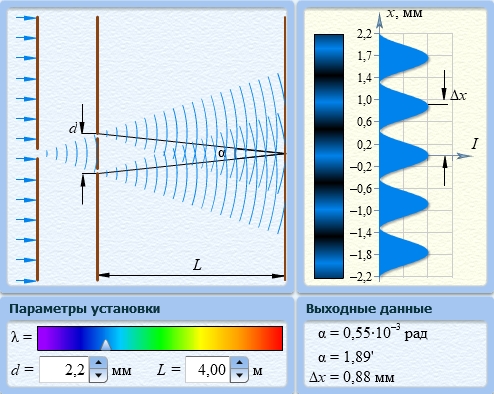
рис.3. Интерференционный опыт Юнга

  1. Щелкая мышью кнопку регулятора расстояния между щелями d, установим минимальное значение d =2,2 мм. Измерим расстояние хтах (в модели просто Δх) между нулевым и первым максимумами («Выходные данные» модели). Результаты эксперимента запишем в таблицу 1.

Таблица 1

Результаты измерений для длины волны голубого цвета при

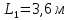
d, мм
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0

хтах, мм
0,80
0,76
0,72
0,70
0,67
0,65
0,62
0,60
0,58

1/d, мм-1
0,45
0,43
0,42
0,40
0,38
0,37
0,36
0,34
0,33

  1. Увеличивая d, измерим еще 9 значений расстояния хтах.

  2. Рассчитаем и внесем в таблицы 1-3 значения обратного расстояния между щелями .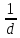

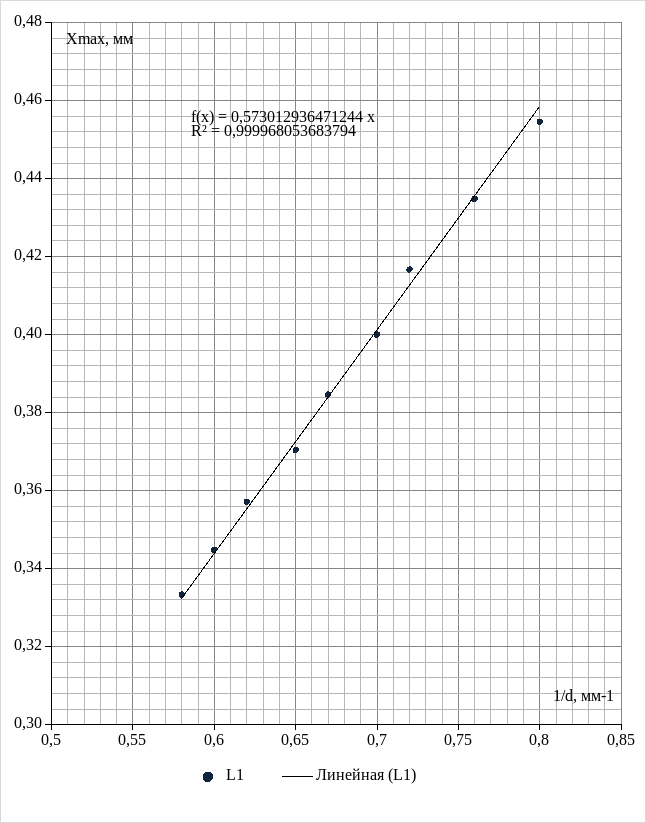
  3. Построим график экспериментальных зависимостей смещения первого максимума xmax от обратного расстояния между щелями.

График экспериментальной зависимости смещения

первого максимума xmax от обратного расстояния между щелями



  1. Проведем аппроксимацию графика прямой линией и определим по графику длину волны .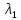





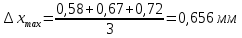
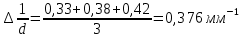
Линейная регрессия:

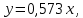где средняя ошибка аппроксимации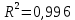



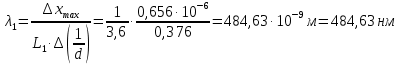
Истинное значение длины волны голубого цвета .

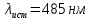Абсолютная погрешность:



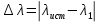
где 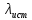- истинное значение, 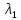-экспериментальное значение.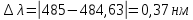



Относительная погрешность



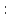
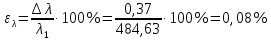
  1. Устанавливая новые значения L, для номера нашей бригады, повторим измерения для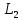 . Результаты всех необходимых величин запишем в таблицу 2.

Таблица 2

Результаты измерений для волны голубого цвета при

d, мм
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0

хтах, мм
0,82
0,78
0,75
0,71
0,69
0,66
0,64
0,62
0,60

1/d, мм-1
0,45
0,43
0,42
0,40
0,38
0,37
0,36
0,34
0,33



  1. Построим график экспериментальных зависимостей смещения первого максимума xmax от обратного расстояния между щелями.

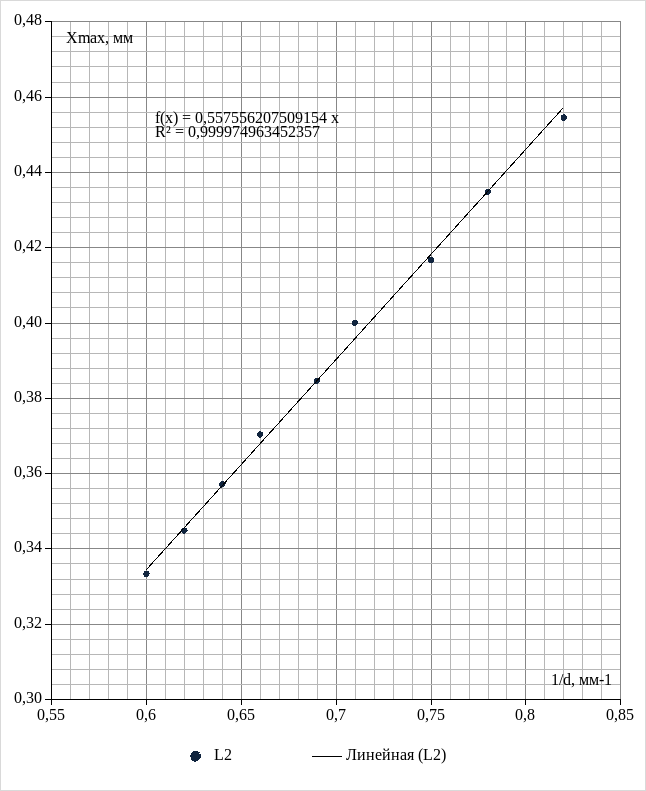
График экспериментальной зависимости смещения

первого максимума xmaxот обратного расстояния между щелями




  1. Проведем аппроксимацию графика прямой линией и определим по графику длину волны .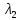





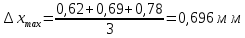
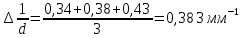
Линейная регрессия:

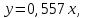где средняя ошибка аппроксимации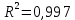



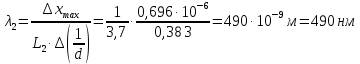
Истинное значение длины волны голубого цвета .

Абсолютная погрешность:



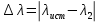
где - истинное значение, 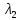- экспериментальное значение.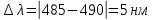



Относительная погрешность



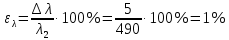
10. Устанавливая новые значения L, для номера нашей бригады, повторим измерения для 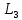. Результаты всех необходимых величин запишем в таблицу 3.

Таблица 3

Результаты измерений для волны голубого цвета при

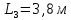
d, мм
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0

хтах, мм
0,82
0,80
0,77
0,73
0,71
0,68
0,66
0,64
0,61

1/d, мм-1
0,45
0,43
0,42
0,40
0,38
0,37
0,36
0,34
0,33

Смотрите также файлы