Файл: Лабораторная работа 1 масштаб топографической карты.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 515
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЗАДАНИЕ 3.
По топографической карте У В (Снов) масштаба 1:50000 измерить малым раствором циркуля-измерителя и курвиметром длину отрезка реки.
а) река Андога от брода южнее Дубасово в кв до устья;
б) река Сысола от истока в кв до южной рамки карты.
Методические указания по выполнению задания.
1. Измерение длины извилистой линии с помощью циркуля-измерителя. Вначале надо выбрать величину раствора циркуля-измерителя. Раствор измерителя (его «шаг») выбирают, исходя из степени извилистости линии: обычно от 2 до 4 мм, увеличивая «шаг» с уменьшением извилистости линии. Установив величину раствора («шага»), проверяют точность установки. Для этого надо «прошагать» по линейке, попеременно переставляя иглы измерителя и не изменяя установленной величины раствора, определенное расстояние, количество «шагов» в котором легко сосчитать (например 8 см содержит 20 шагов по 4 мм). При необходимости корректируют установленный раствор. Далее «шагают» по заданной линии, учитывая все извилины (при этом подсчитывается число «шагов»). Десятые доли последнего «шага» оцениваются на глаз. По окончании измерения снова с помощью линейки необходимо проверить величину раствора измерителя и, убедившись в том, что оно не изменилось, провести для контроля измерение в обратном направлении. Из полученных значений нужно вычислить среднее и рассчитать относительную ошибку измерений. При допустимой ошибке надо цену одного «шага» измерителя умножить на среднее число «шагов». Например, в результате двух измерений длины реки раствором измерителя 2 мм по карте масштаба 1: получилось 35,9 и 36,5 «шагов». Среднее значение равно 36,2 мм. Относительная ошибка: (36,5-35,9) : 36,2 = 0,6/36,2 = 1/60. Ошибка допустима. Расстояние в 2 мм на карте масштаба 1: равно 100 м на местности. Следовательно цена одного «шага» измерителя равна 100 м. Длину реки в метрах получают, умножив цену «шага» на среднее количество «шагов» измерителя: 100 м х 36,2 ш = 3620 м или 3,62 км.
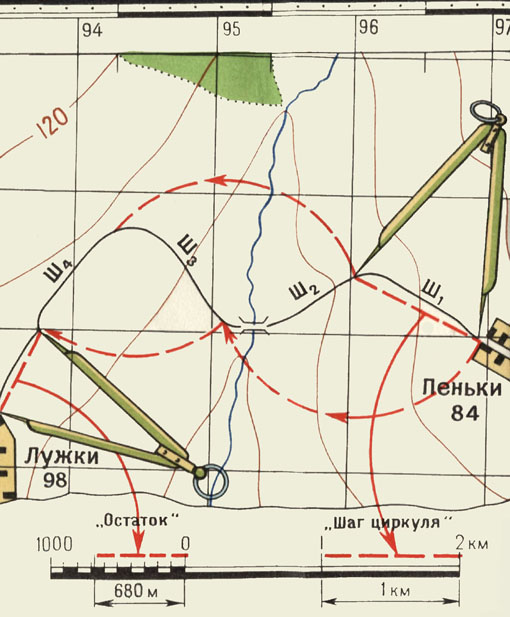
Рис. 2
2. Измерение длины извилистой линии с помощью курвиметра. Перед измерением длины линии по карте нужно определить цену деления курвиметра расстояние на карте, которое соответствует наименьшему делению шкалы циферблата курвиметра. Для этого надо провести курвиметр по линейке или по линии равной 10 см. Убедитесь, что стрелка прибора отклонится на 10 делений. Следовательно, 1 деление шкалы курвиметра соответствует 1 см. Для измерения заданной линии установить курвиметр в ее начальной точке и, взяв отсчет по циферблату, провести прибором вдоль линии так, чтобы показания стрелки возрастали (курвиметр должен находиться постоянно в вертикальном положении, колесико плотно соприкасаться с бумагой и вращаться, а не скользить). В конечной точке линии снова взять отсчет по соответствующей шкале циферблата и вычислить разность двух отсчетов. Для контроля следует заданную линию измерить в обратном направлении, вычислить среднее значение из двух измерений и относительную ошибку. Длина заданной линии равна цене деления курвиметра умноженной на среднее из двух измерений по курвиметру.
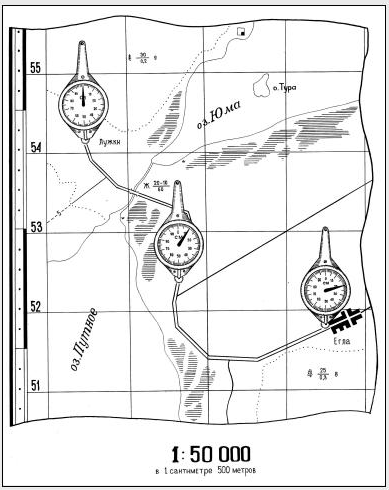
Рис.3
ЗАДАНИЕ 3. По топографической карте У В-в-4 масштаба 1:50000 определить графическим (геометрическим) способом площадь соснового леса «Северный» в кв. 6812,
Методические указания по выполнению задания.
Чтобы определить площадь участка на карте, его нужно разделить на геометрические фигуры (квадраты, трапеции, треугольники и др.). Объект с криволинейным контуром можно разбить на геометрические фигуры, предварительно спрямив границы. Спрямление производится с таким расчетом, чтобы сумма отрезанных участков и сумма избытков взаимно компенсировали друг друга. Площадь каждой фигуры вычисляется отдельно по геометрическим формулам 1 в единицах измерения, применяемых на карте (в квадратных сантиметрах). Затем определяется общая площадь участка, равная сумме площадей всех фигур. Повторное измерение площади участка производится по геометрическим фигурам в другой комбинации. Расхождения между двумя значениями площади участка не должно превышать 2% от вероятнейшего значения площади. То есть, относительная ошибка должна быть равна или меньше 1/50 (методику расчета см. в задании 2). При допустимой ошибке рассчитывают площадь заданного участка: S леса = m х S леса на карте, (где m величина масштаба площади, S леса на карте среднее значение из двух измерений площади участка). При измерении площадей необходимо пользоваться масштабом площадей. Для этого надо перевести именованный масштаб длин в именованный масштаб площадей. Например, если в 1 см на карте содержится 500 метров, то 1 кв. см соответствует кв. м (500 м х 500 м), или 25 га (1 га кв. м), или 0,25 кв. км.
ЗАДАНИЕ 4. По топографической карте У В (Снов) масштаба 1:50000 определить с помощью сеточной палетки площадь смешанного леса в кв. 7020, 7019, 7120, По этой же карте определить, пользуясь километровой сеткой, площадь смешанного леса, расположенного севернее населенного пункта Калитино (кв. 7514). 1 S прямоугольника. = ab (где a и b стороны прямоугольника); S квадрата = a2 (где a сторона квадрата); S параллелограмма = ah (где a основание, h высота); S треугольника = 1/2 ah (где а основание, h высота); S трапеции = ( a + b)/2 h (где a и b основания, h высота); S круга = πr 2 (где R радиус круга) ;
Методические указания по выполнению задания
Перед измерением площади с помощью палетки необходимо определить цену деления палетки число квадратных метров или гектаров, соответствующее одному делению палетки, для карты данного масштаба, то есть площадь каждого квадратика в поземельных мерах. На карте в масштабе 1:10 000, при условии, что стороны квадратов палетки равны 2 мм: С (цена деления палетки) = 20 м х 20 м = 400 м 2 = 4 сотки (в 1 см 100 м, в 1 мм 10 м, в 2 мм 20 м). Палетку накладывают на измеряемый участок и подсчитывают вначале число целых квадратов, заключенных внутри контура участка, затем число неполных квадратов, внутри контура. К количеству полных квадратов нужно прибавить половину общего количества неполных квадратов. N 1 (N 2 ) = n полных кв. + 1/2 n неполных кв. Измерение повторить при ином положении палетки относительно измеряемого участка. Расхождение между двумя полученными значениями (относительная ошибка) не должно превышать 1/50 измеренной площади. При соблюдении этого условия, за окончательное принимают среднее из двух значений. Площадь участка равна произведению цены деления палетки на число всех квадратов: S участка = C х (N среднее )
Задание 5.
По топографической карте У В (Снов) масштаба 1:50000 определить площадь смешанного леса в кв. 7020, 7019, 7120, сеханическим способом ( с помощью планиметра.
Методические указания по выполнению задания.
Механический способ определения площадей.
Определение площадей механическим способом производится при помощи планиметров. Наибольшее распространение получил полярный планиметр (рисунок 4), состоящий из полюсного и обводного рычагов.

Рис.4
Полюсный рычаг на одном конце имеет груз с короткой иглой (полюсом), а на другом – штифт, который соединяется с обводным рычагом. На конце обводного рычага имеется обводной шпиль (или лупа), которым обводят измеряемую площадь. На обводном рычаге расположен счетный механизм, состоящий из счетного колеса, разделенного на 100 частей. Ось вращения колеса сопряжена при помощи червячной передачи с циферблатом, разделенным по окружности на 10 частей и снабженным указателем для снятия отсчета. Червячная передача устроена так, что одному обороту колеса соответствует поворот циферблата на одно деление. Рядом с колесом находится верньер, по которому отсчитывают десятые доли делений колеса или тысячные доли его оборота.Полный отсчет, выраженный в тысячных долях оборота колеса, состоит из четырех цифр, первая из которых берется по указателю циферблата, вторая и третья – по нулевому штриху верньера с ободка колесика. Четвертая отсчитывается по верньеру.
При определении площади фигуры устанавливают планиметр полюсом внутри или вне контура фигуры, а обводной шпиль ставят над какой-либо точкой контура и делают отсчет по счетному механизму U1. После этого тщательно обводят шпилем по ходу часовой стрелки контур фигуры и делают второй отсчет U2. Площадь Р при полюсе вне фигуры вычисляют по формуле
Р = С(U2 – U1),
где С – цена деления планиметра;
При определении площадей планиметром необходимо соблюдать следующие правила:
- план или карта, по которому определяют площади, должен быть хорошо разглажен и натянут на ровном гладком столе;
- положение полюса планиметра выбирают так, чтобы при обводе данной фигуры не образовывались весьма острые или тупые углы между рычагами планиметра и чтобы счетное колесо при этом не сходило с листа бумаги;
- обводной шпиль следует вести по контуру плавно, выбирая все изгибы контура. Начальную точку выбирают в таком месте, в котором при обводе счетное колесо почти не вращается;
- для контроля и уточнения результатов каждый контур обводят два раза в прямом и обратном направлениях и берут среднее из результатов.
Точность определения площадей планиметром зависит от формы и размера обводимой фигуры, состояния плана и других причин. Для фигур средней величины (10–30 см2) ошибка определения площади планиметром не превышает 1:200 величины площади.
Вычисление площадей аналитическим способом
Аналитические способы определения площади применяют для замкнутых плоских многоугольников, в которых известны координаты х и у всех вершин (к таким многоугольникам относятся граница населенного пункта, промышленного, сельскохозяйственного или горно-добывающего предприятия, контур лесного массива, озера, болота и т.д.).
| Площадь замкнутого многоугольника вычисляют по различным формулам аналитической геометрии, наиболее распространены следующие: | | |
| n | n | |
| 2Р = ∑ х i (уi+1 – уi-1); | 2Р = ∑ у i (хi-1 – хi+1); i = 1, 2, , n, | |
| i | i | |
т.е. удвоенная площадь многоугольника равна сумме произведений каждой абсциссы на разность ординат передней и задней по ходу точек, а также сумме произведений каждой ординаты на разность абсцисс задней и передней по ходу точек. Например, для многоугольника 1-2-3-4
2Р = х1 (у2 – у4) + х2 (у3 – у1) + х3 (у4 – у2) + х4 (у1 – у3);
2Р = у1 (х4 – х2) + у2 (х1 – х3) + у3 (х2 – х4) + у4 (х3 – х1);
Площадь вычисляют отдельно по каждой формуле (15.3) с промежуточным контролем разностей координат на условие
| n | n | |
| ∑(уi+1 – уi-1) = 0; | ∑(хi-1 – хi+1) = 0, i = 1, 2, …, n. | |
| i | i | |
Точность расчетов по формулам определяется погрешностями координат. Например, если координаты вершин многоугольника получены теодолитным ходом, то площадь участка получается с относительной погрешностью 1/500 – 1/2000. В случае неверно записанного значения хотя бы одной из координат хi или уi получается ошибочное значение площади при полном совпадении результатов расчетов по формулам. Такую ошибку можно обнаружить, например, по чрезмерному расхождению между площадью многоугольника и суммой площадей контуров внутри него, нанесенных на план и измеренных планиметром.