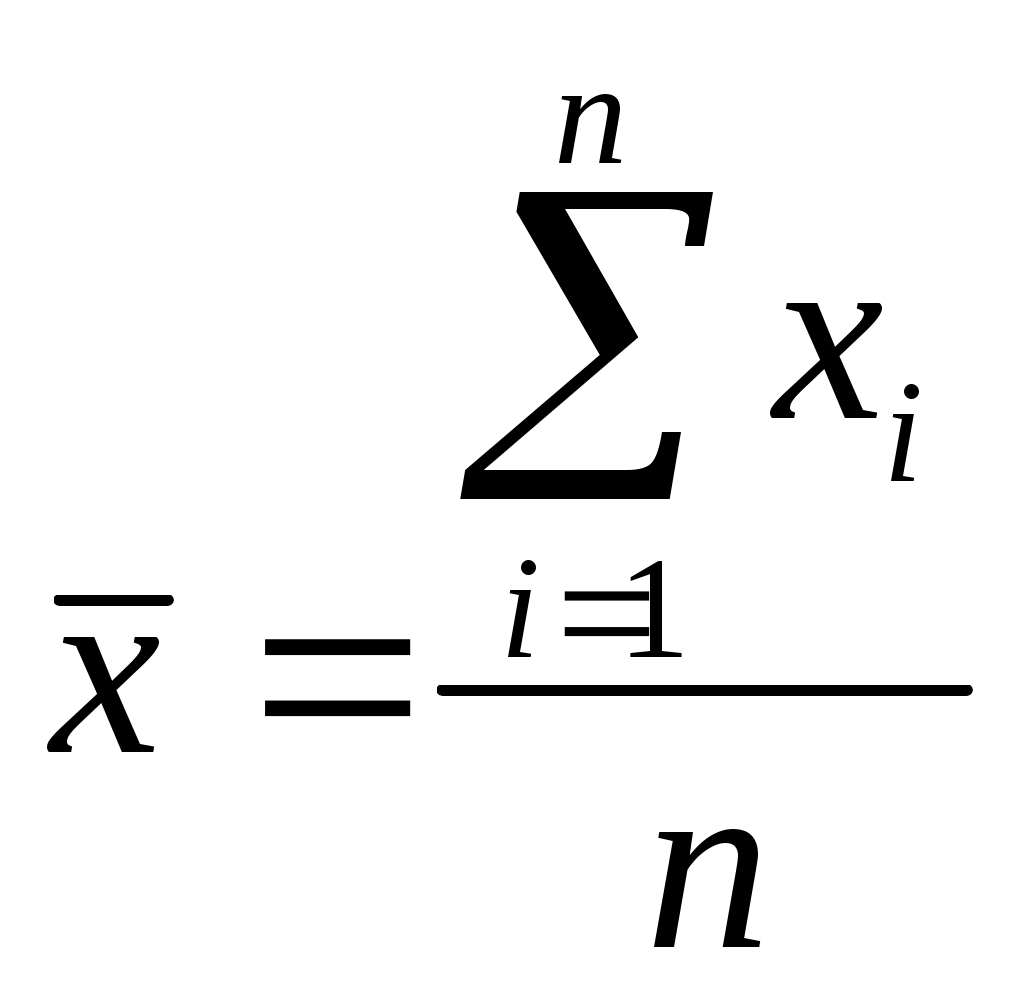Группы субъектов РФ по потребительским расходам в среднем на душу населения (в месяц), руб.	Число субъектов в группе
7207 - 11657	2
11657 - 16107	10
16107 - 20557	14
20557 - 25007	10
25007 - 29457	3
29457 - 33907	1
Итого	40

2. По полученному в результате группировки ряду распределения постройте гистограмму распределения, полигон распределения и кумуляту.

Наглядно ряды распределения представляются при помощи графических изображений. Ряды распределения изображаются в виде: полигона, гистограммы, кумуляты.

Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс (х) откладываются значения варьирующего признака, а по оси ординат (y) - частоты или частости. Полученные на пересечении абсцисс и ординат точки соединяются прямыми линиями, в результате этого получают ломаную линию, называемую полигоном распределения.

Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными на соответствующих интервалах. Высота столбиков в случае равных интервалов должна быть пропорциональна частотам.

Гистограмма может быть преобразована в полигон распределения, если найти середины сторон прямоугольников и затем эти точки соединить прямыми линиями.

При помощи кумуляты (кривой сумм) изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам и показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.

Пример оформления исходных данных для построения графиков представлен в таблице 3 Примеры графиков представлены на рисунках 4, 5, 6.

---

Таблица 3 – Данные для построения графиков

Группы субъектов РФ по потребительским расходам в среднем на душу населения (в месяц), руб.	Число субъектов в группе	Середина интервала	Верхние границы интервалов	Накопленные частоты
7207 - 11657	2	9432	11657	2
11657 - 16107	10	13882	16107	12
16107 - 20557	14	18332	20557	26
20557 - 25007	10	22782	25007	36
25007 - 29457	3	27232	29457	39
29457 - 33907	1	31682	33907	40
Итого	40	-	-	-

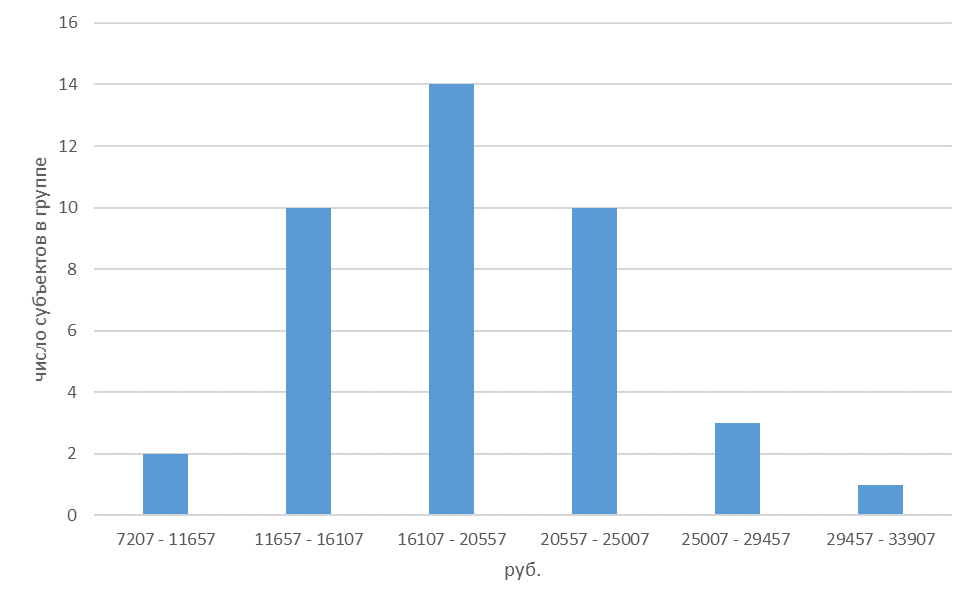
Рисунок 4 – Гистограмма распределения субъектов РФ по потребительским расходам в среднем на душу населения (в месяц)

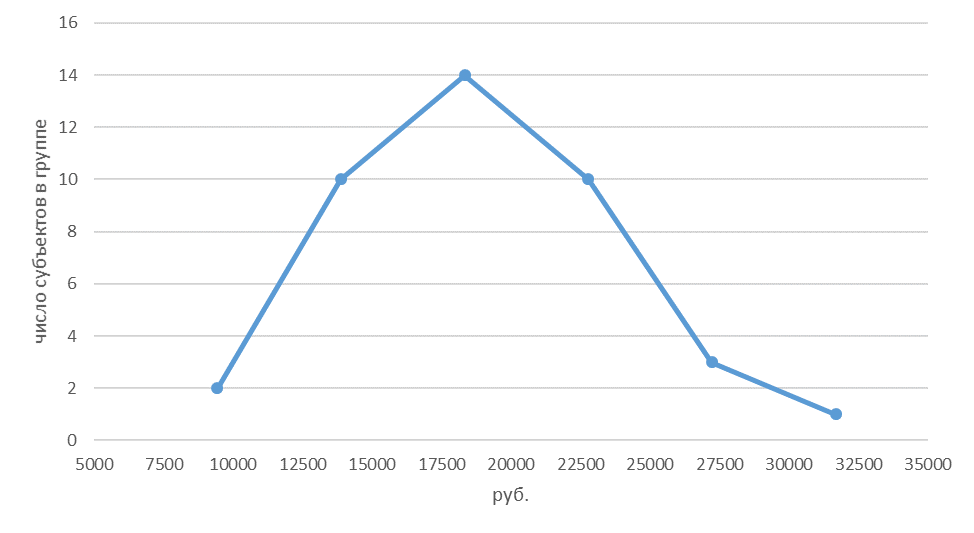Рисунок 5 – Полигон распределения субъектов РФ по потребительским расходам в среднем на душу населения (в месяц)
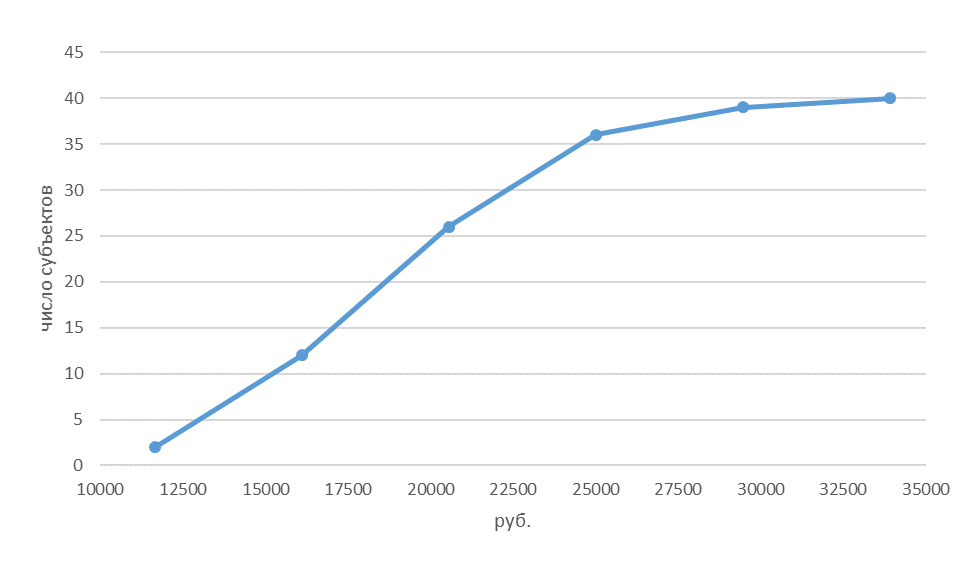Рисунок 6 – Кумулята распределения субъектов РФ по потребительским расходам в среднем на душу населения (в месяц)
3. В составленном интервальном вариационном ряду определить:

а) относительные величины структуры по группам; полученные значения изобразить на графике в виде секторной диаграммы;

б) относительные величины интенсивности: объем ВРП в рублях в расчете на душу населения по группам и в целом по совокупности.

Произведите анализ полученных данных.
Относительные величины представляют собой результат деления одного абсолютного показателя на другой и характеризуют количественное соотношение между ними. При расчете относительных величин в

---

числителе всегда находится сравниваемый показатель, а в знаменателе – показатель, с которым производится сравнение, т.е. принимаемый за основание или базу сравнения. Все используемые на практике относительные статистические величины можно подразделить на следующие виды: динамики, структуры, координации, интенсивности, сравнения, плана и реализации плана.

Относительные величины структуры (ОВС) представляют собой соотношение структурных частей изучаемого объекта и их целого:
.
Выражается ОВС в долях единицы или процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какой долей обладает или какой удельный вес имеет та или иная часть в общем итоге.

Пример оформления результатов расчетов ОВС представлен в таблице 4.
Таблица 4 – Структура субъектов РФ по потребительским расходам

Группы субъектов РФ по потребительским расходам в среднем на душу населения (в месяц), руб.	Число субъектов в группе	ОВС,%
7207 - 11657	2	5,0
11657 - 16107	10	25,0
16107 - 20557	14	35,0
20557 - 25007	10	25,0
25007 - 29457	3	7,5
29457 - 33907	1	2,5
Итого	40	100,0

Пример графического изображения ОВС представлен на рисунке 7.



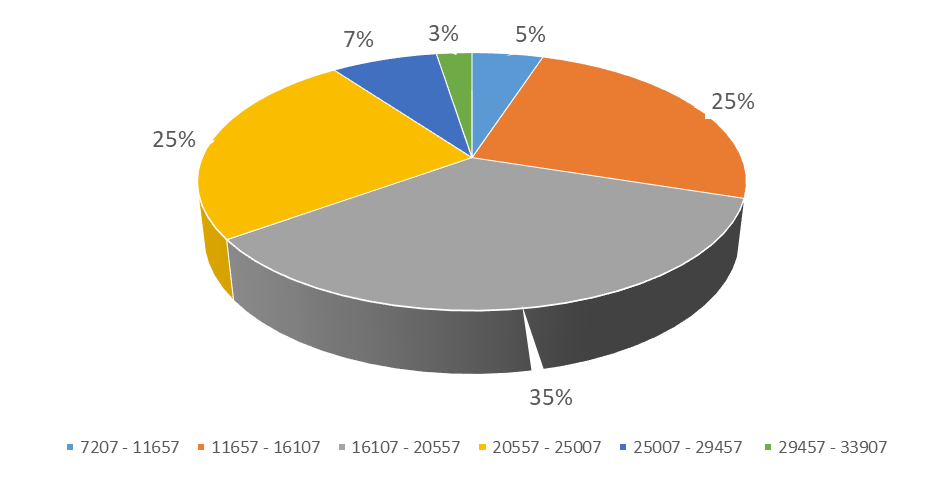
Рисунок 7 – Структура субъектов РФ по потребительским расходам
в среднем на душу населения (в месяц)
Относительные величины интенсивности (ОВИ) характеризуют степень распространения изучаемого явления и представляют собой отношение исследуемого показателя к размеру присущей ему среды:
.
Данные показатели получают сопоставлением разноименных, но взаимосвязанных величин. Поэтому наиболее часто они представляют собой именованные величины. Обычно ОВИ рассчитывают в тех случаях, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, плотности его распространения.

---

Пример оформления расчетов ОВИ представлен в таблице 5.

---

Таблица 5 – Расчет объема ВРП на душу населения, тыс. руб./чел.

Группы субъектов РФ по потребительским расходам в среднем на душу населения (в месяц), руб.	Число субъектов в группе	Численность населения, тыс. чел.	Объем ВРП, млн. руб.	ОВИ, тыс.руб./чел.
7207 - 11657	2	758,3	101622,1	134,0
11657 - 16107	10	15628,6	3959115,4	253,3
16107 - 20557	14	18244,5	5999687,8	328,8
20557 - 25007	10	25933,4	9471433,3	365,2
25007 - 29457	3	1866,0	1264974,4	677,9
29457 - 33907	1	487,4	829298,6	1701,5
Итого	40	62918,2	21626131,6	343,7

4. По выборочной совокупности рассчитайте среднюю величину группировочного признака, моду, медиану, квартили. Произведите анализ полученных данных.
Средняя величина – это обобщающая количественная характеристика уровня варьирующего признака по однородной совокупности. Средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения. В зависимости от характера изучаемых явлений, от конкретных задач и целей статистического исследования применяются четыре вида средних: арифметическая; гармоническая; геометрическая; квадратическая. Наиболее широкое применение и, следовательно, распространение имеет средняя арифметическая.

Средняя арифметическая простая рассчитывается для несгруппированных данных, представляющих собой n значений признака x:

---

Смотрите также файлы

• 4. Охрана труда.docx

• Понятие и структура системы таможеннотарифного регулирования.docx

• Занятие 3.docx

• Реферат Лечебная физическая культура при беременности.docx

• Отчет по Практической работе 4 по дисциплине Введение в специальность.docx