Файл: Методические рекомендации по выполнению курсового проекта по дисциплине Статистика по направлению 38. 03. 02 Менеджмент по профилям подготовки Финансовый менеджмент.doc
Добавлен: 22.11.2023
Просмотров: 52
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Средняя арифметическая взвешенная рассчитывается по сгруппированным данным: дискретным и интервальным вариационным рядам:
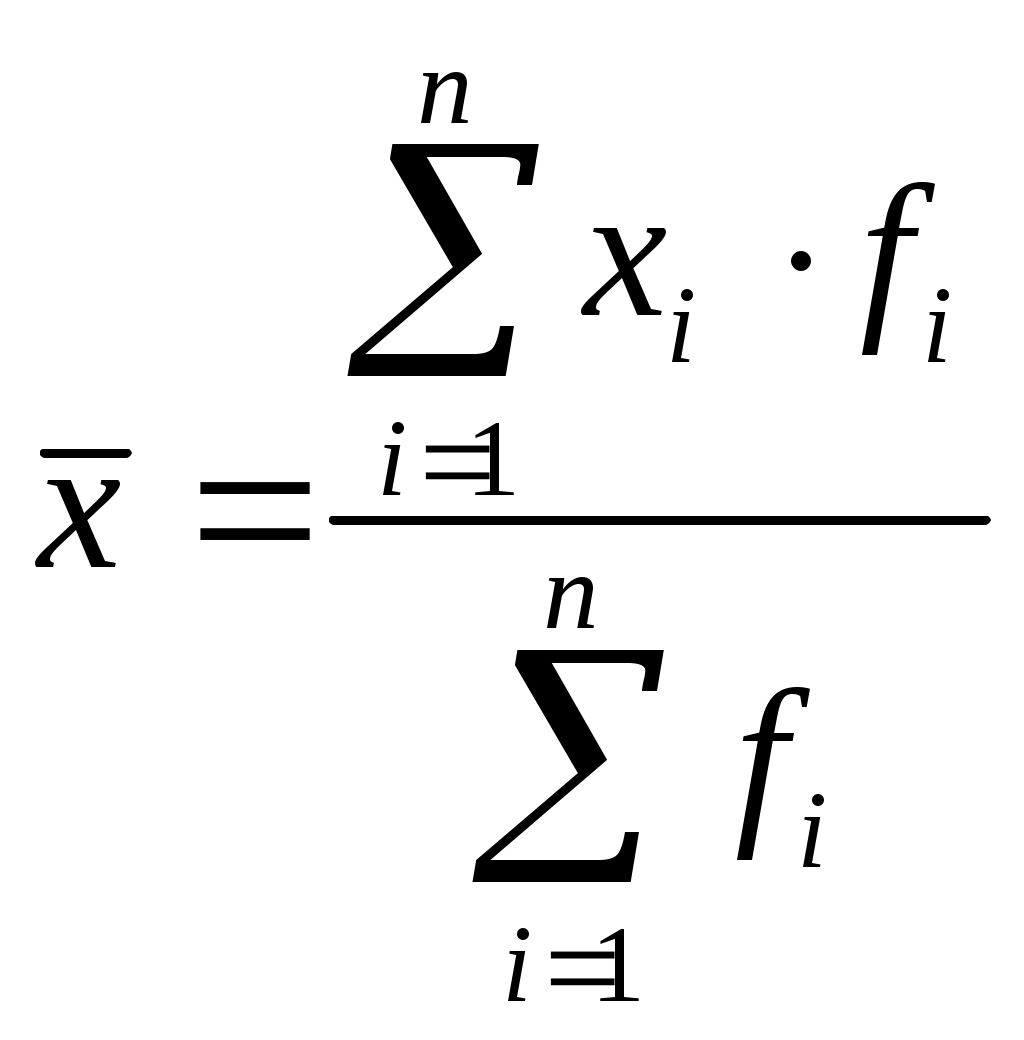 .
.
где xi – варианта, индивидуальное значение признака;
n – число вариант;
fi – вес, частота, число единиц совокупности с данным значением признака.
Пример оформления расчетов для нахождения средней величины представлен в таблице 6.
Таблица 6 – Данные для расчета средней величины
По данным таблицы средняя величина будет равна:
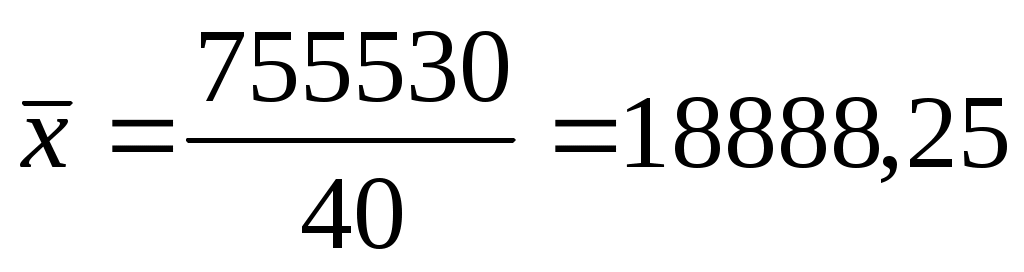 руб.
руб.
Модой в статистике называют значение признака, наиболее часто встречающееся в исследуемой совокупности.
Для нахождения моды в интервальном вариационном ряду сначала определяется модальный интервал, т.е. содержащий моду – интервал с наибольшей частотой. Конкретное значение моды для интервального ряда определяется по формуле:
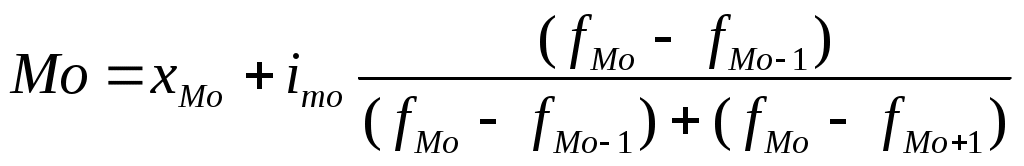 ,
,
где xMo – нижняя граница модального интервала;
iMo – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала
, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для нахождения медианы в интервальном вариационном ряду определяются накопленные частоты, по данным о накопленных частотах находят медианный интервал – интервал, в котором накопленная частота составляет половину или впервые превышает половину всей суммы частот. Формула для определения медианы в интервальном ряду распределения имеет следующий вид:
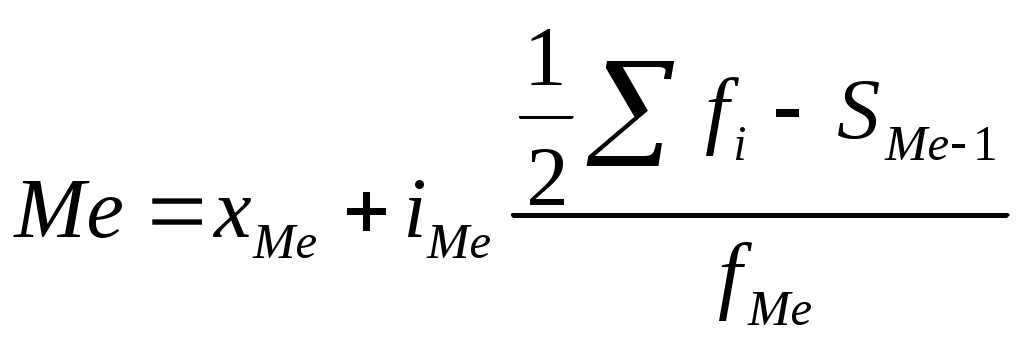 .
.
где xMe – нижняя граница медианного интервала;
iMe – величина медианного интервала;
∑fi – сумма частот ряда;
SMe-1 – сумма накопленных частот интервала, предшествующего медианному;
fMe – частота медианного интервала.
Квартили – значения признака, делящие ранжированную совокупность на четыре равные части. Различают квартиль нижний (Q1), средний (Q2) и верхний (Q3). Нижний квартиль отделяет 1/4 часть совокупности с наименьшими значениями признака, верхний - 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% – между Q2 и Q3; остальные 25% превосходят Q3. Средним квартилем (Q2) является медиана.
Для расчета квартилей по интервальному ряду используют формулы:
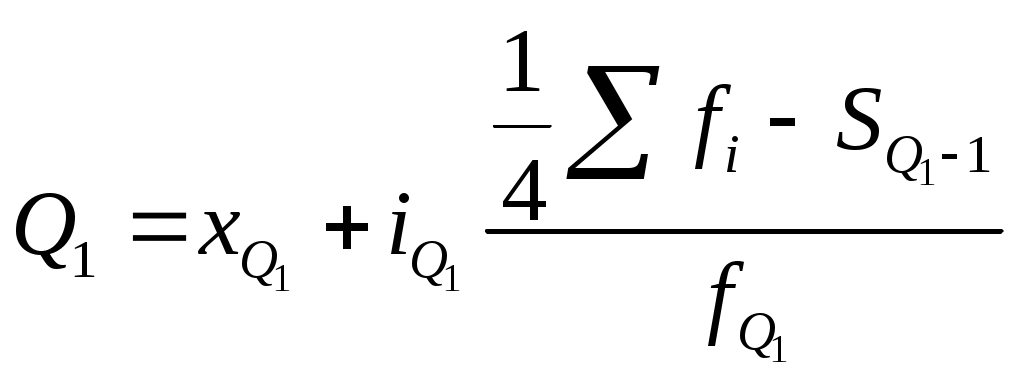 ;
;
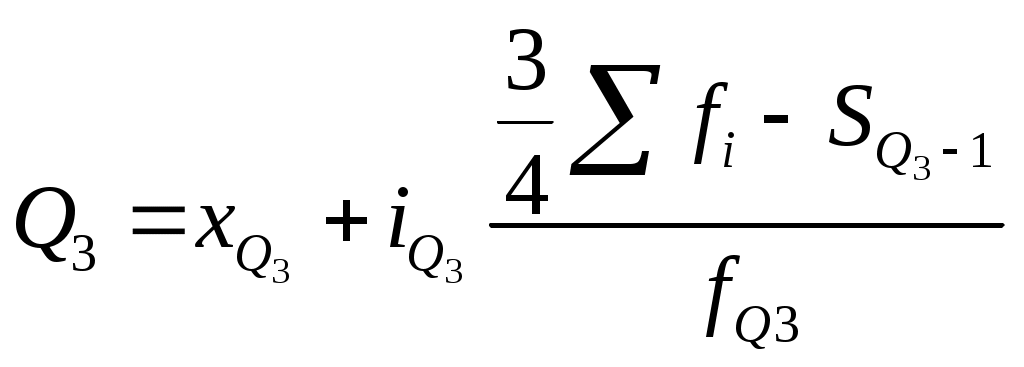 .
.
где xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
SQ1-1 – накопленная частота интервала, предшествующего интервалу
, содержащему нижний квартиль;
SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
fQ1 – частота интервала, содержащего нижний квартиль;
fQ3 – частота интервала, содержащего верхний квартиль.
Пример расчетов моды, медианы и квартилей представлены в таблице 7 и ниже.
Таблица 7 – Данные для расчета структурных средних величин
В нашем примере модальный интервал от 16107 до 20557 руб. Определили по наибольшей частоте – 14. Медианный интервал - от 16107 до 20557 руб. Определили по накопленной частоте, впервые превышающей половину суммы всех частот – 26 впервые превышает 20. Первый квартиль находится в интервале от 11657 до 16107 руб. Определили по накопленной частоте, первой превышающей ¼ суммы всех частот - 12 впервые превышает 10. Второй квартиль находится в интервале от 16107 до 20557 руб., совпадает с медианой. Третий квартиль находится в интервале от 20557 до 25007 руб. Определили по накопленной частоте, первой превышающей 3/4 суммы всех частот - 36 впервые превышает 30.
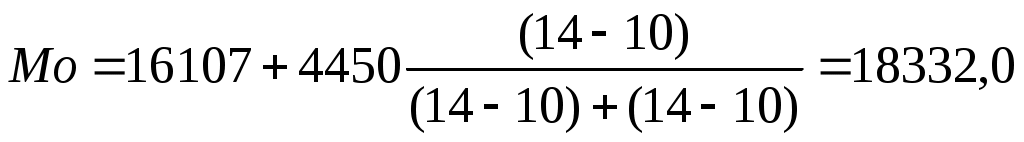 руб.
руб.
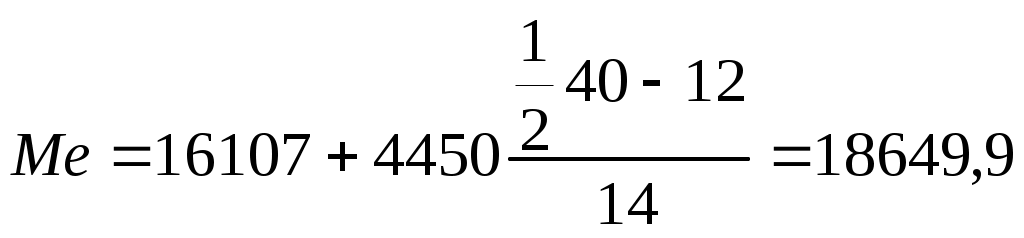 руб.
руб.
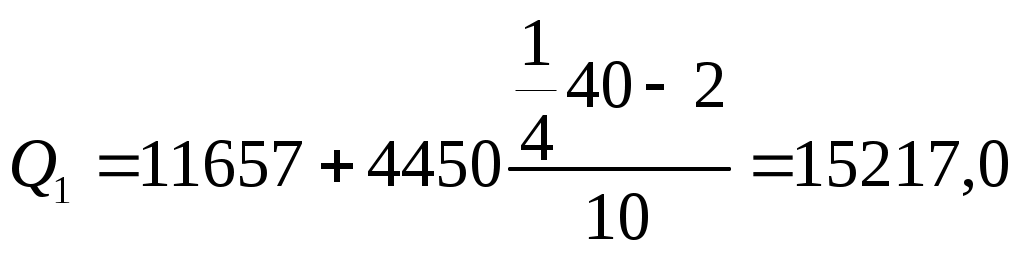 руб.
руб.
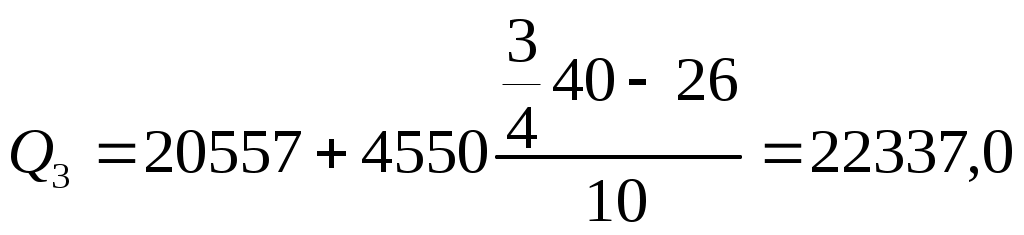 руб.
руб.
5. По выборочной совокупности (интервальному вариационному ряду распределения) определите показатели вариации: размах вариации, среднее линейное отклонение, дисперсию; среднее квадратическое отклонение и коэффициент вариации. Сделайте выводы по полученным данным.
Показатели вариации измеряют изменение значения признака отдельных единиц относительно среднего их значения. Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. К относительным показателям вариации относятся: коэффициенты вариации, осцилляции, относительное линейное отклонение и др.
Размах вариации (R) представляет собой разность между максимальным (xmax) и минимальным (xmin) значением признака исследуемой совокупности:
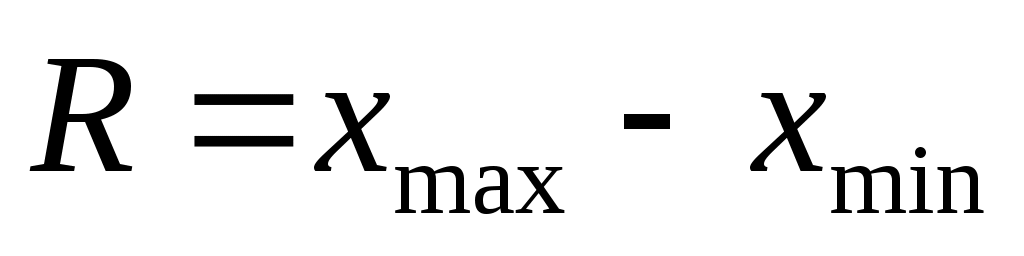 .
.
Среднее линейное отклонение – это среднее из абсолютных отклонений значений признака от средней арифметической:
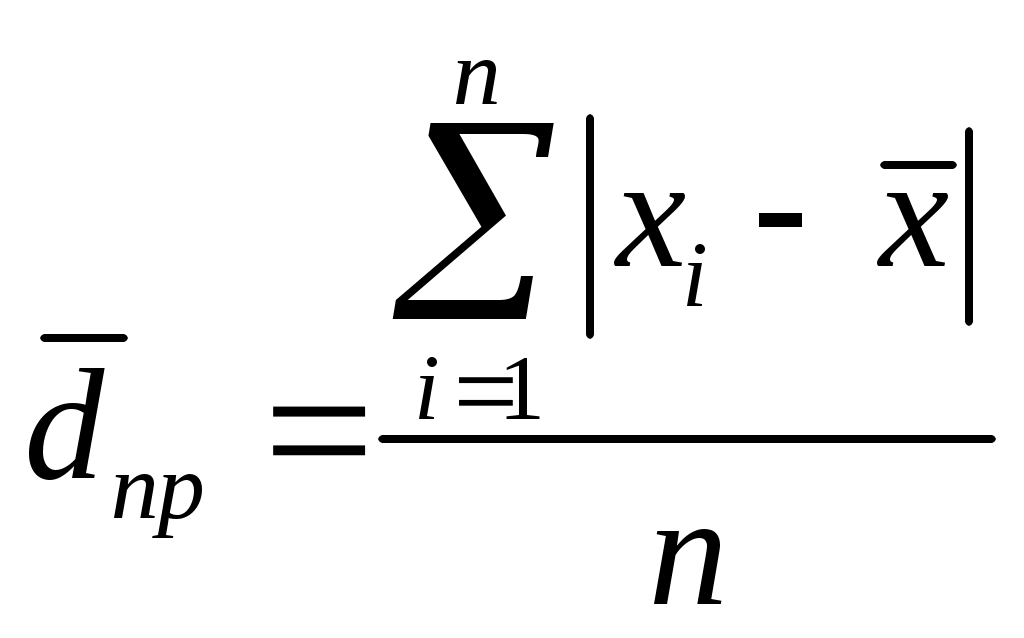 ,
, 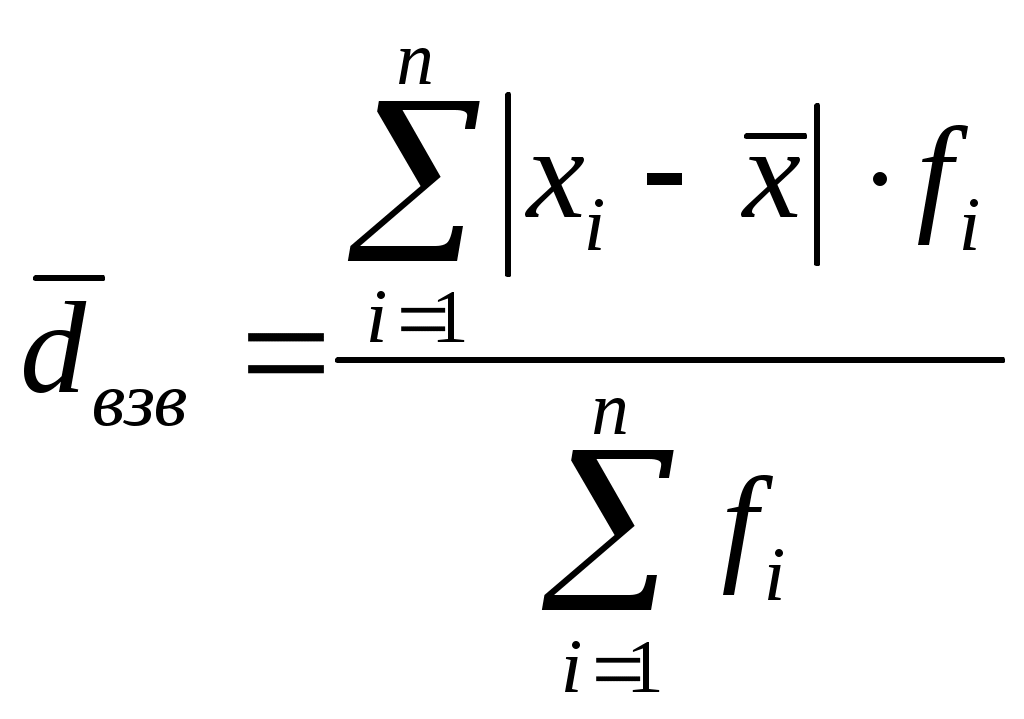 .
.
Дисперсия – это среднее из квадратов отклонений индивидуальных значений признака от средней величины:
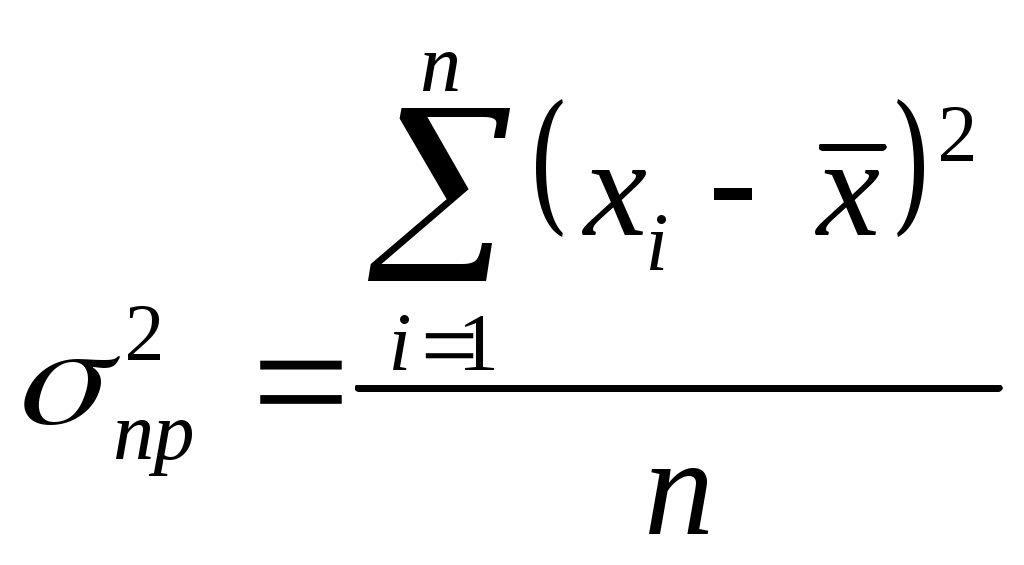 ,
, 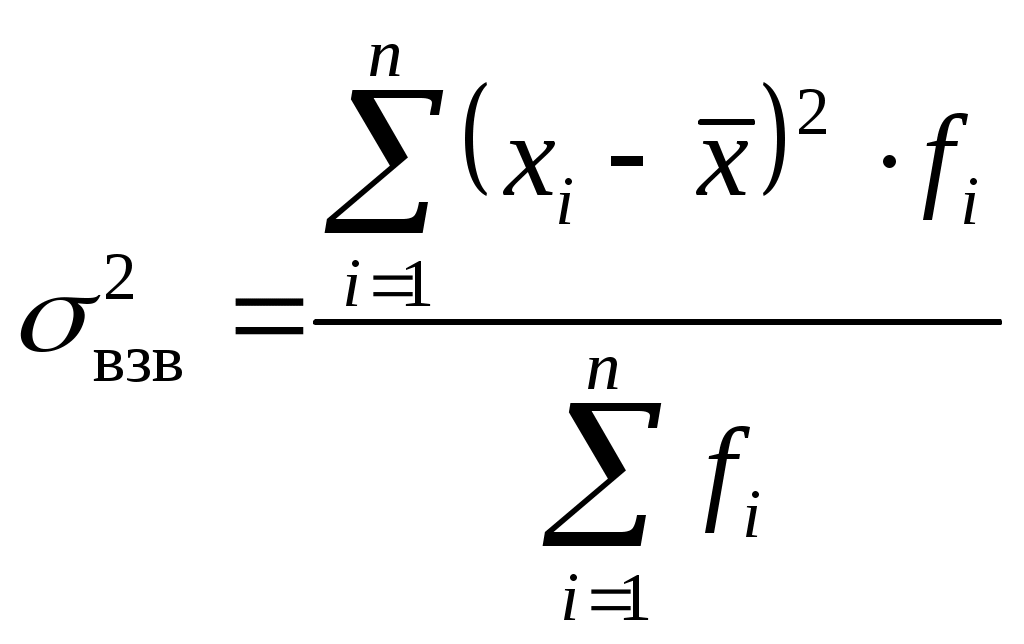 .
.
Среднее квадратическое отклонение находится как корень из дисперсии. Показывает (как и среднее линейное отклонение) на сколько в среднем индивидуальные значения признака отклоняются от средней арифметической:
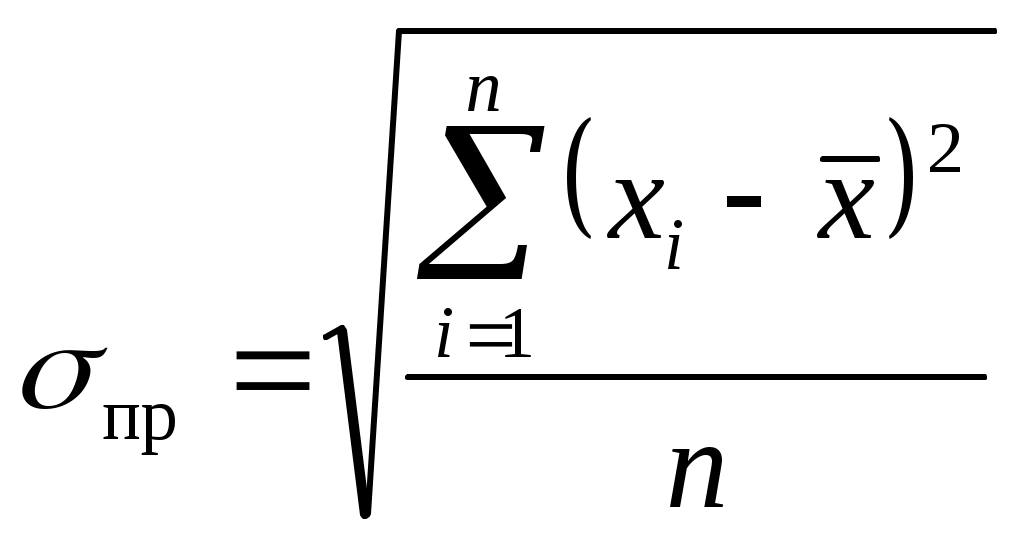 ,
, 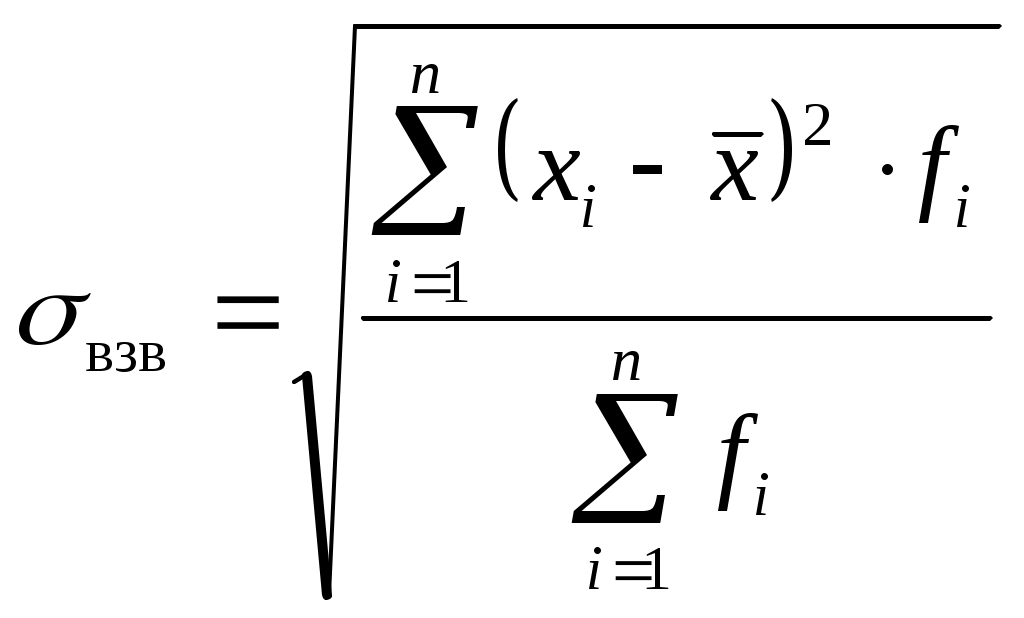 .
.
Коэффициент вариации – это относительный показатель, исчисляемый как отношение среднего квадратического отклонения к средней арифметической:
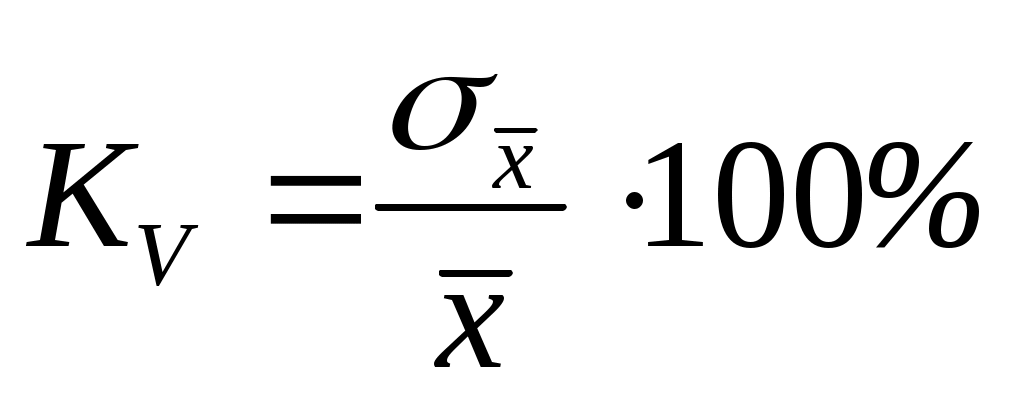 .
.
Считается, что если коэффициент вариации превышает 33%, то совокупность нельзя признать качественно однородной. Если Kv ≤ 33%, то можно утверждать, что совокупность более или менее однородна, а, следовательно, средняя, рассчитанная по такой совокупности, типична.
Пример расчетов показателей вариации представлен в таблице 8 и ниже.
Таблица 8 – Данные для расчета показателей вариации
Размах вариации: R = 33907 – 7207 = 26700 руб.
Среднее значение: руб.
руб.
Среднее линейное отклонение: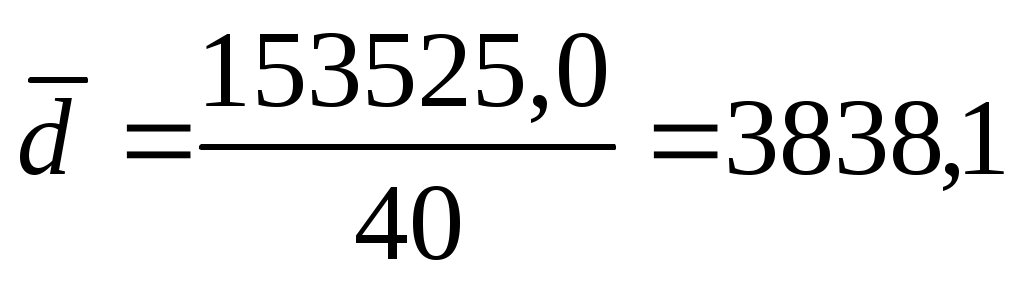 руб.
руб.
Дисперсия: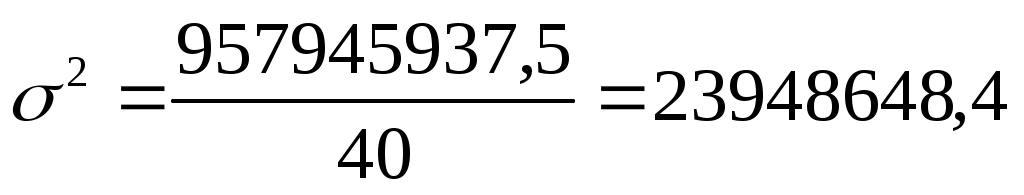
Среднее квадратическое отклонение: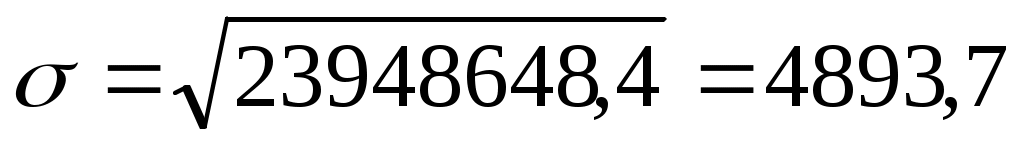
Средняя арифметическая взвешенная рассчитывается по сгруппированным данным: дискретным и интервальным вариационным рядам:
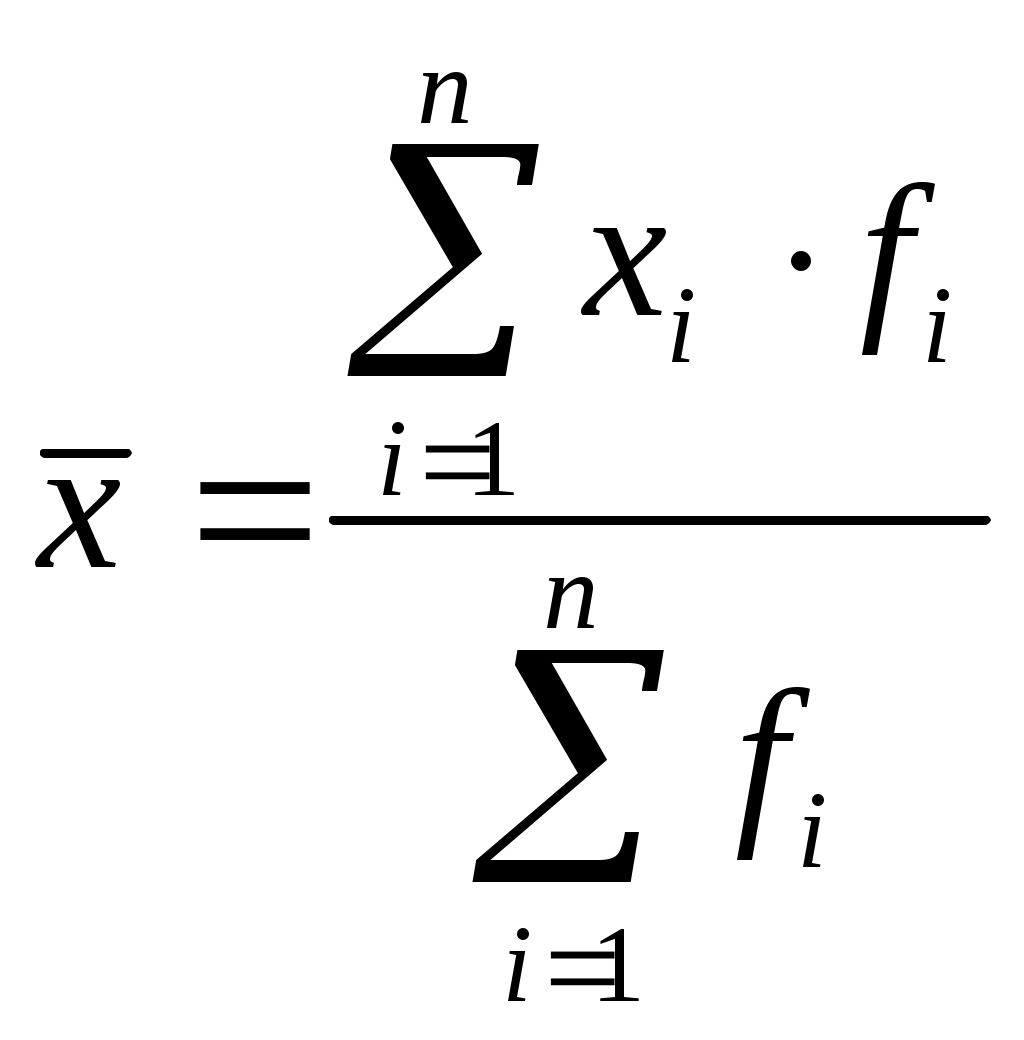 .
.где xi – варианта, индивидуальное значение признака;
n – число вариант;
fi – вес, частота, число единиц совокупности с данным значением признака.
Пример оформления расчетов для нахождения средней величины представлен в таблице 6.
Таблица 6 – Данные для расчета средней величины
| Группы субъектов РФ по потребительским расходам в среднем на душу населения (в месяц), руб. | Число субъектов в группе | Середина интервала | xifi |
| 7207 - 11657 | 2 | 9432 | 18864 |
| 11657 - 16107 | 10 | 13882 | 138820 |
| 16107 - 20557 | 14 | 18332 | 256648 |
| 20557 - 25007 | 10 | 22782 | 227820 |
| 25007 - 29457 | 3 | 27232 | 81696 |
| 29457 - 33907 | 1 | 31682 | 31682 |
| Итого | 40 | - | 755530 |
По данным таблицы средняя величина будет равна:
Модой в статистике называют значение признака, наиболее часто встречающееся в исследуемой совокупности.
Для нахождения моды в интервальном вариационном ряду сначала определяется модальный интервал, т.е. содержащий моду – интервал с наибольшей частотой. Конкретное значение моды для интервального ряда определяется по формуле:
где xMo – нижняя граница модального интервала;
iMo – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала
, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
Для нахождения медианы в интервальном вариационном ряду определяются накопленные частоты, по данным о накопленных частотах находят медианный интервал – интервал, в котором накопленная частота составляет половину или впервые превышает половину всей суммы частот. Формула для определения медианы в интервальном ряду распределения имеет следующий вид:
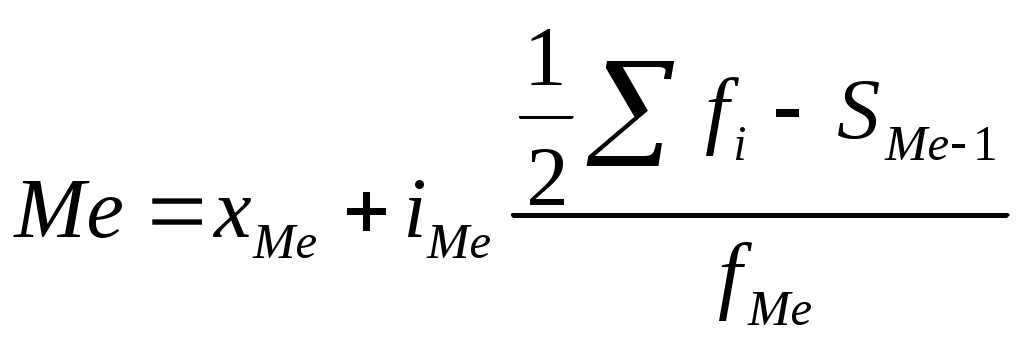 .
.где xMe – нижняя граница медианного интервала;
iMe – величина медианного интервала;
∑fi – сумма частот ряда;
SMe-1 – сумма накопленных частот интервала, предшествующего медианному;
fMe – частота медианного интервала.
Квартили – значения признака, делящие ранжированную совокупность на четыре равные части. Различают квартиль нижний (Q1), средний (Q2) и верхний (Q3). Нижний квартиль отделяет 1/4 часть совокупности с наименьшими значениями признака, верхний - 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% – между Q2 и Q3; остальные 25% превосходят Q3. Средним квартилем (Q2) является медиана.
Для расчета квартилей по интервальному ряду используют формулы:
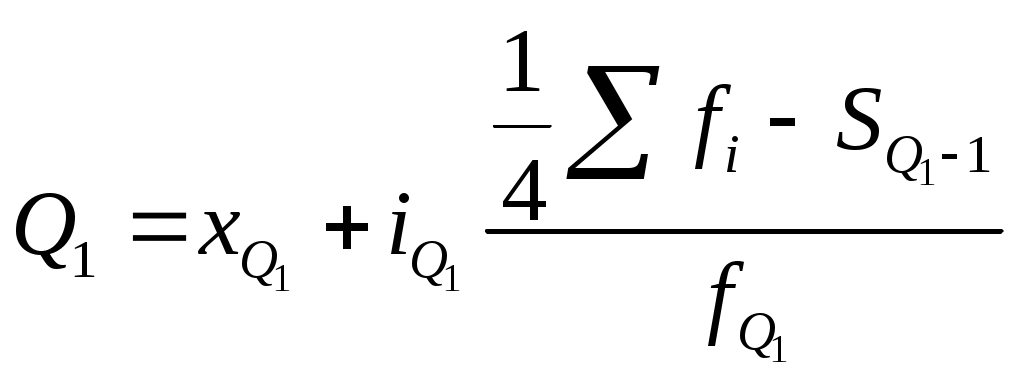 ;
;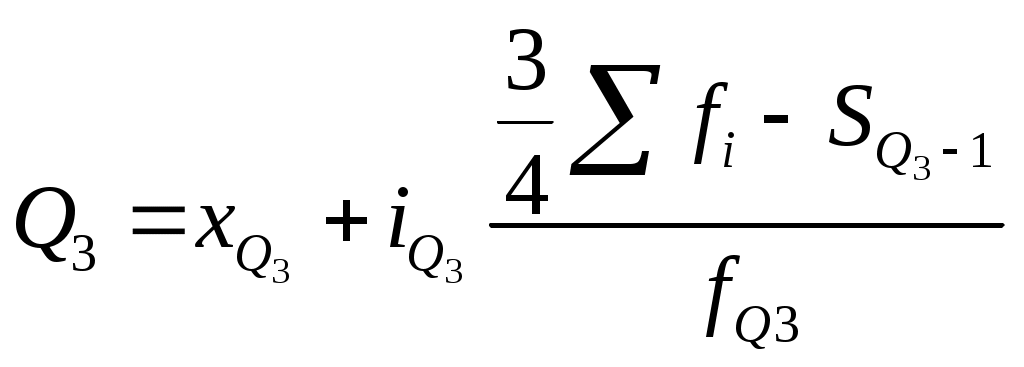 .
.где xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
SQ1-1 – накопленная частота интервала, предшествующего интервалу
, содержащему нижний квартиль;
SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
fQ1 – частота интервала, содержащего нижний квартиль;
fQ3 – частота интервала, содержащего верхний квартиль.
Пример расчетов моды, медианы и квартилей представлены в таблице 7 и ниже.
Таблица 7 – Данные для расчета структурных средних величин
| Группы субъектов РФ по потребительским расходам в среднем на душу населения (в месяц), руб. | Число субъектов в группе | Накопленные частоты |
| 7207 - 11657 | 2 | 2 |
| 11657 - 16107 | 10 | 12 |
| 16107 - 20557 | 14 | 26 |
| 20557 - 25007 | 10 | 36 |
| 25007 - 29457 | 3 | 39 |
| 29457 - 33907 | 1 | 40 |
| Итого | 40 | - |
В нашем примере модальный интервал от 16107 до 20557 руб. Определили по наибольшей частоте – 14. Медианный интервал - от 16107 до 20557 руб. Определили по накопленной частоте, впервые превышающей половину суммы всех частот – 26 впервые превышает 20. Первый квартиль находится в интервале от 11657 до 16107 руб. Определили по накопленной частоте, первой превышающей ¼ суммы всех частот - 12 впервые превышает 10. Второй квартиль находится в интервале от 16107 до 20557 руб., совпадает с медианой. Третий квартиль находится в интервале от 20557 до 25007 руб. Определили по накопленной частоте, первой превышающей 3/4 суммы всех частот - 36 впервые превышает 30.
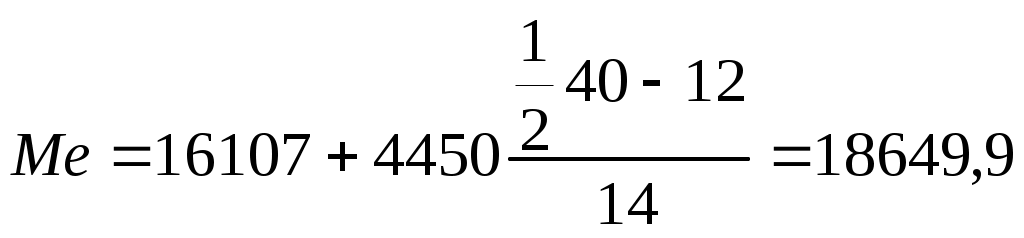 руб.
руб.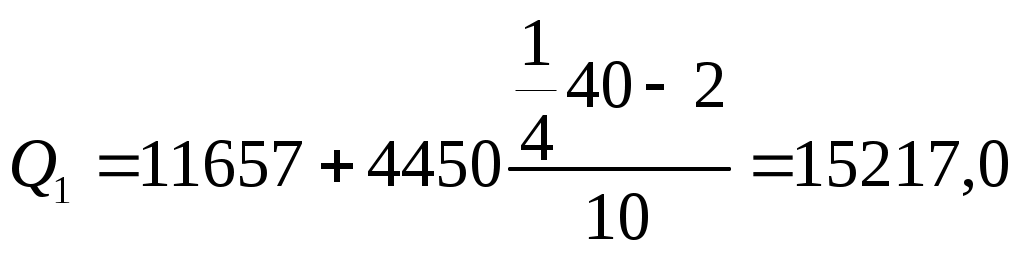 руб.
руб.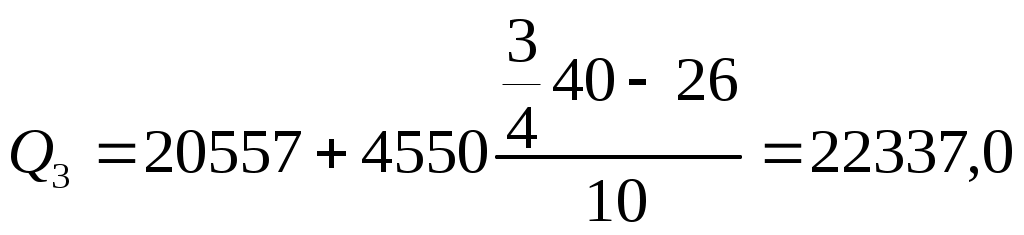 руб.
руб.5. По выборочной совокупности (интервальному вариационному ряду распределения) определите показатели вариации: размах вариации, среднее линейное отклонение, дисперсию; среднее квадратическое отклонение и коэффициент вариации. Сделайте выводы по полученным данным.
Показатели вариации измеряют изменение значения признака отдельных единиц относительно среднего их значения. Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. К относительным показателям вариации относятся: коэффициенты вариации, осцилляции, относительное линейное отклонение и др.
Размах вариации (R) представляет собой разность между максимальным (xmax) и минимальным (xmin) значением признака исследуемой совокупности:
Среднее линейное отклонение – это среднее из абсолютных отклонений значений признака от средней арифметической:
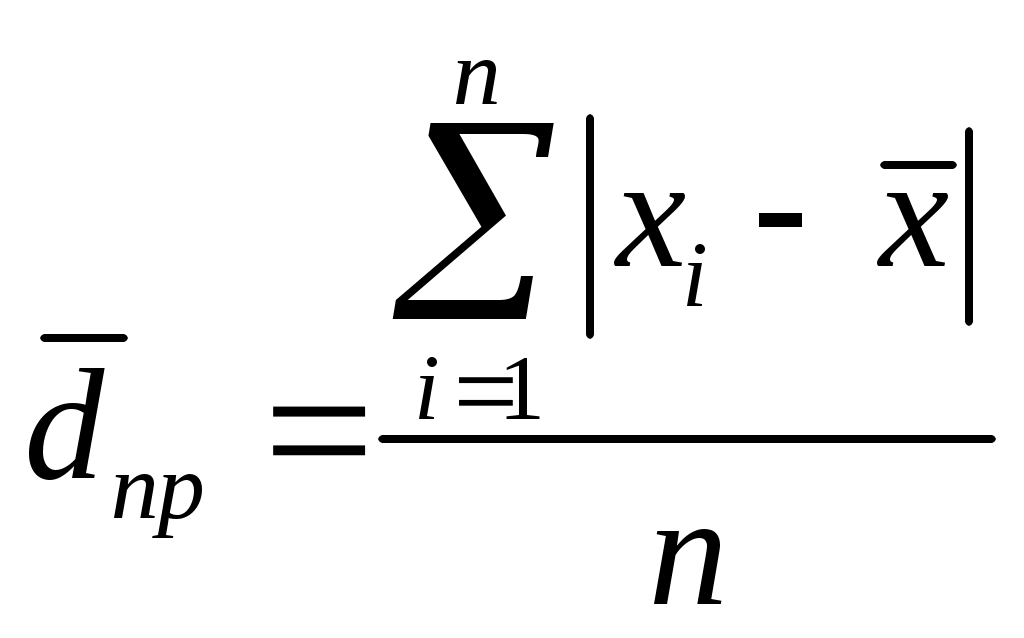 ,
, 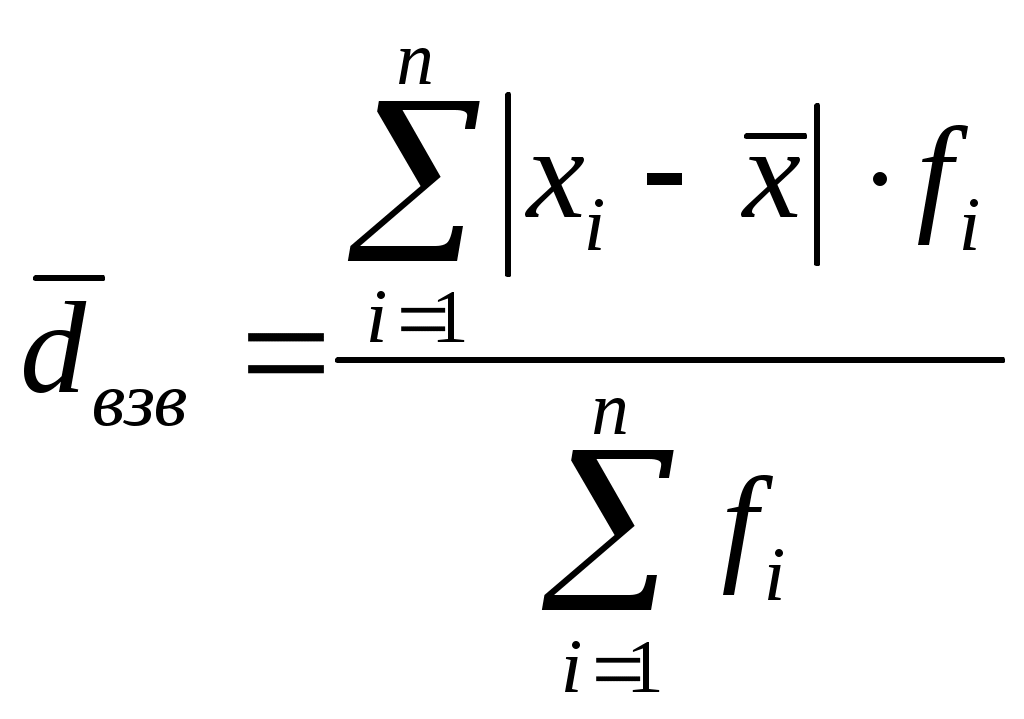 .
.Дисперсия – это среднее из квадратов отклонений индивидуальных значений признака от средней величины:
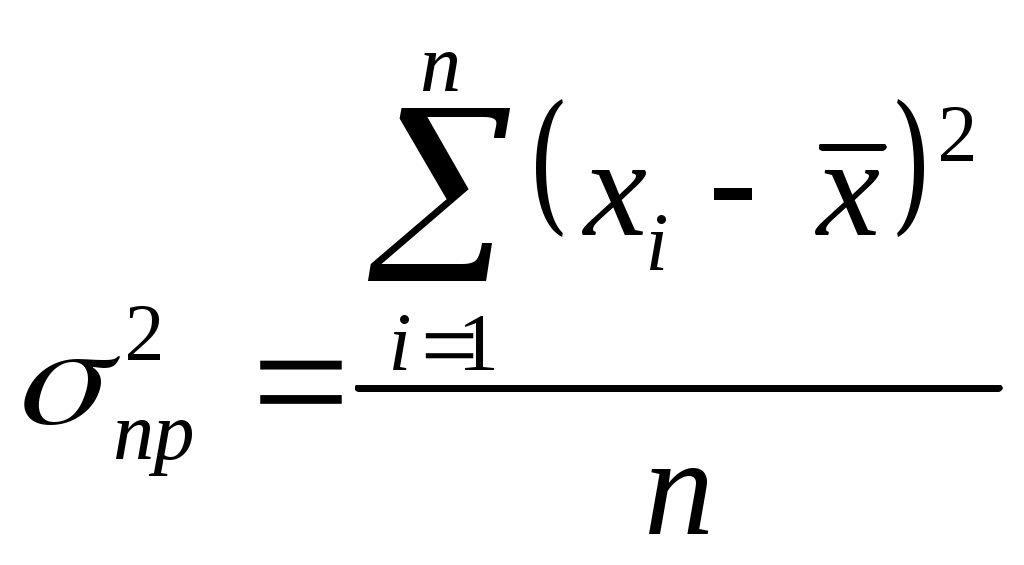 ,
, 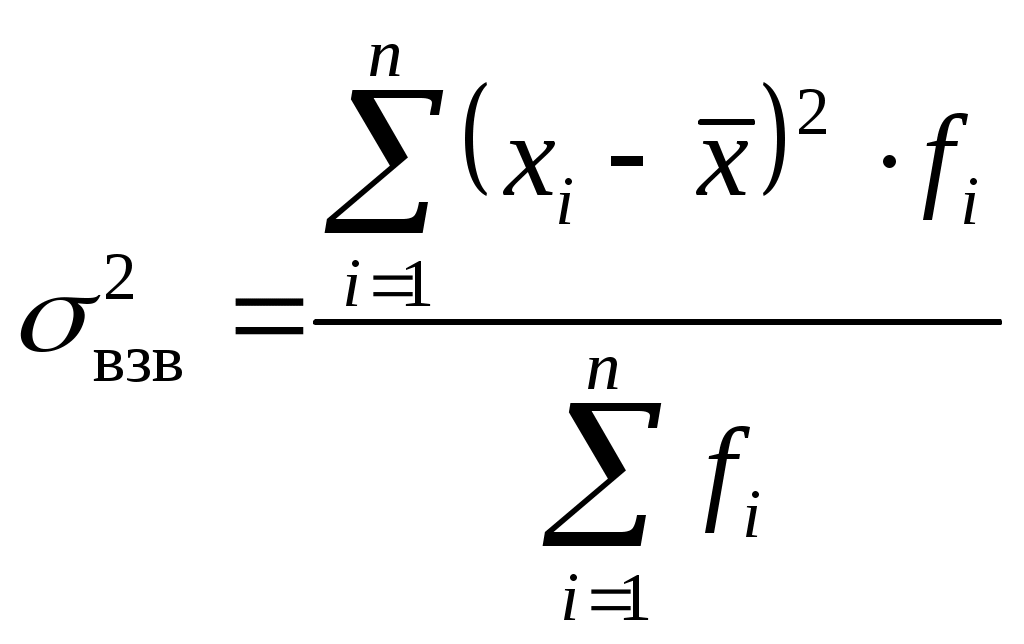 .
.Среднее квадратическое отклонение находится как корень из дисперсии. Показывает (как и среднее линейное отклонение) на сколько в среднем индивидуальные значения признака отклоняются от средней арифметической:
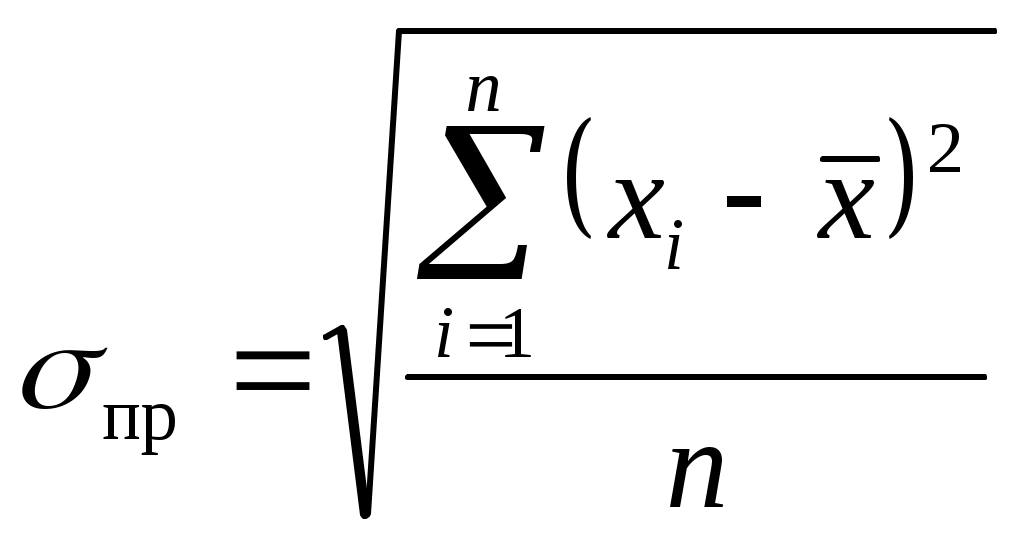 ,
, 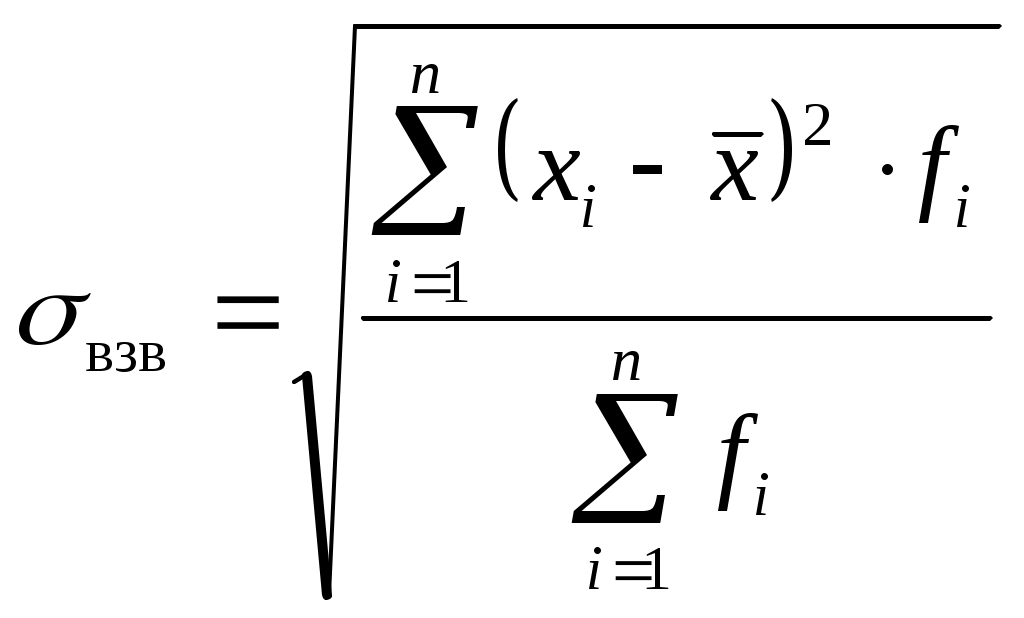 .
.Коэффициент вариации – это относительный показатель, исчисляемый как отношение среднего квадратического отклонения к средней арифметической:
Считается, что если коэффициент вариации превышает 33%, то совокупность нельзя признать качественно однородной. Если Kv ≤ 33%, то можно утверждать, что совокупность более или менее однородна, а, следовательно, средняя, рассчитанная по такой совокупности, типична.
Пример расчетов показателей вариации представлен в таблице 8 и ниже.
Таблица 8 – Данные для расчета показателей вариации
| Группы субъектов РФ по потребительским расходам в среднем на душу населения (в месяц), руб. | Число субъектов в группе | Середина интервала | xifi | | | | |
| 7207 - 11657 | 2 | 9432 | 18864 | 9456,3 | 18912,5 | 89420664,1 | 178841328,1 |
| 11657 - 16107 | 10 | 13882 | 138820 | 5006,3 | 50062,5 | 25062539,1 | 250625390,6 |
| 16107 - 20557 | 14 | 18332 | 256648 | 556,3 | 7787,5 | 309414,1 | 4331796,9 |
| 20557 - 25007 | 10 | 22782 | 227820 | 3893,8 | 38937,5 | 15161289,1 | 151612890,6 |
| 25007 - 29457 | 3 | 27232 | 81696 | 8343,8 | 25031,3 | 69618164,1 | 208854492,2 |
| 29457 - 33907 | 1 | 31682 | 31682 | 12793,8 | 12793,8 | 163680039,1 | 163680039,1 |
| Итого | 40 | - | 755530 | - | 153525,0 | - | 957945937,5 |
Размах вариации: R = 33907 – 7207 = 26700 руб.
Среднее значение:
Среднее линейное отклонение:
Дисперсия:
Среднее квадратическое отклонение: