Файл: Методические рекомендации по выполнению курсового проекта по дисциплине Статистика по направлению 38. 03. 02 Менеджмент по профилям подготовки Финансовый менеджмент.doc
Добавлен: 22.11.2023
Просмотров: 50
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
руб.
Коэффициент вариации: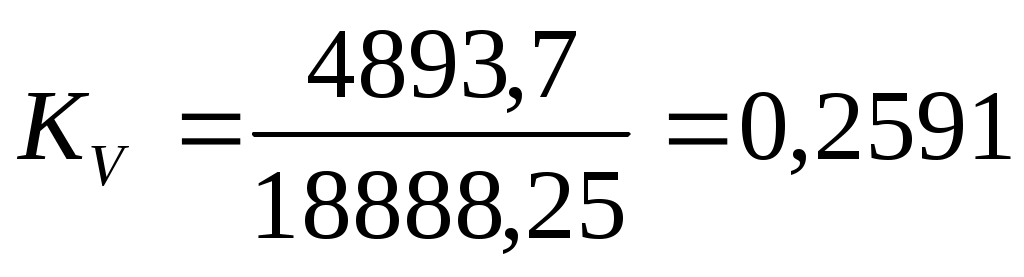
или 25,91%
6. Определить с доверительной вероятностью 0,954 возможные пределы колебаний средней величины группировочного признака в генеральной совокупности.
Выборочное наблюдение – несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.
Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей. Генеральная совокупность – исходная изучаемая статистическая совокупность, из которой производится отбор части единиц. Выборочная совокупность (выборка) – отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию.
Отбор единиц в выборочную совокупность может быть:
1) повторным;
2) бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора.
При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует, т.е. не возвращается обратно.
Средняя ошибка выборки определяется по следующим формулам:
а) при повторном отборе
,
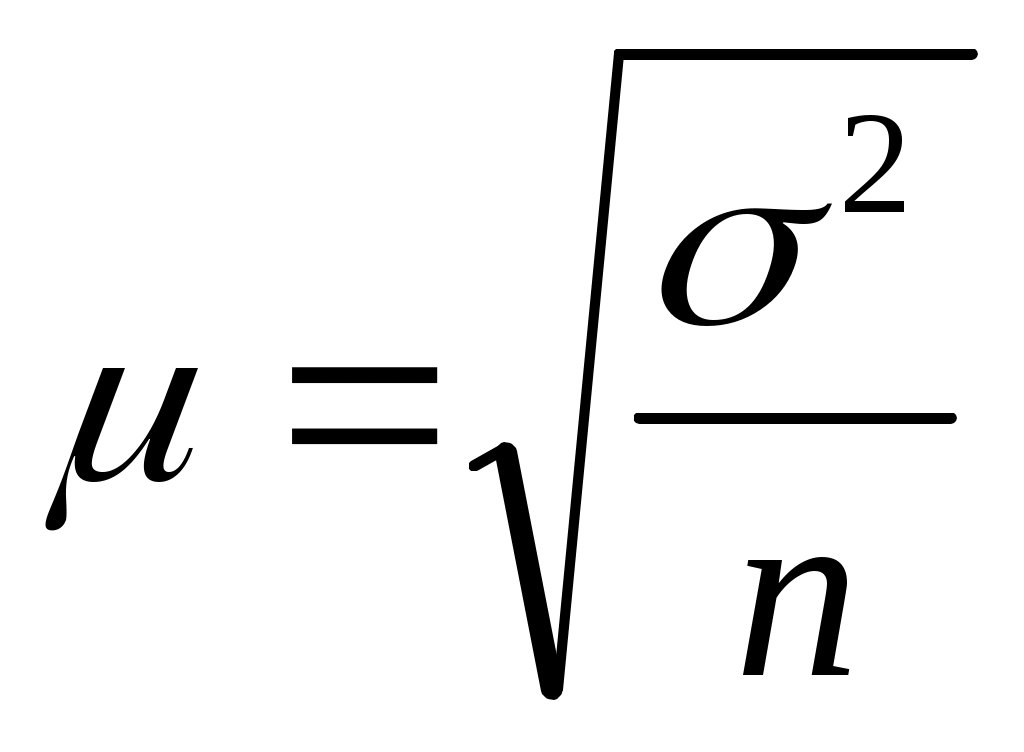где μ – средняя ошибка выборки;
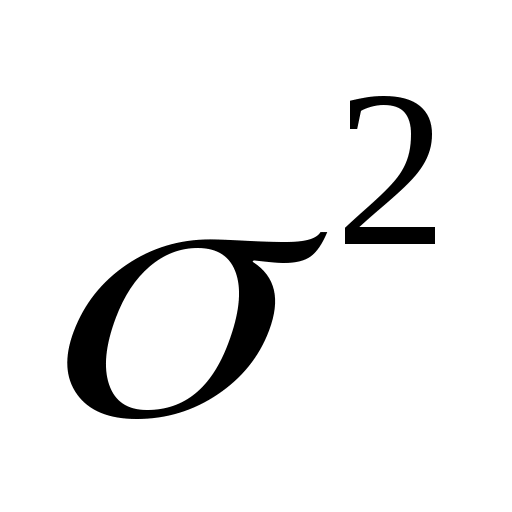– дисперсия выборочной совокупности;
n – объем (число единиц) выборочной совокупности;
б) при бесповторном отборе:
,
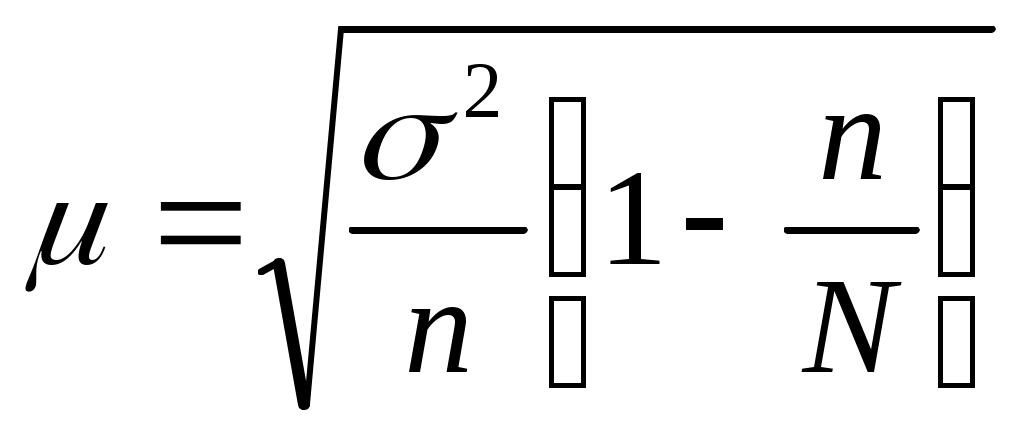где N – число единиц в генеральной совокупности.
При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности
, с которым гарантируется, что генеральная средняя не выйдет за указанные границы:
,
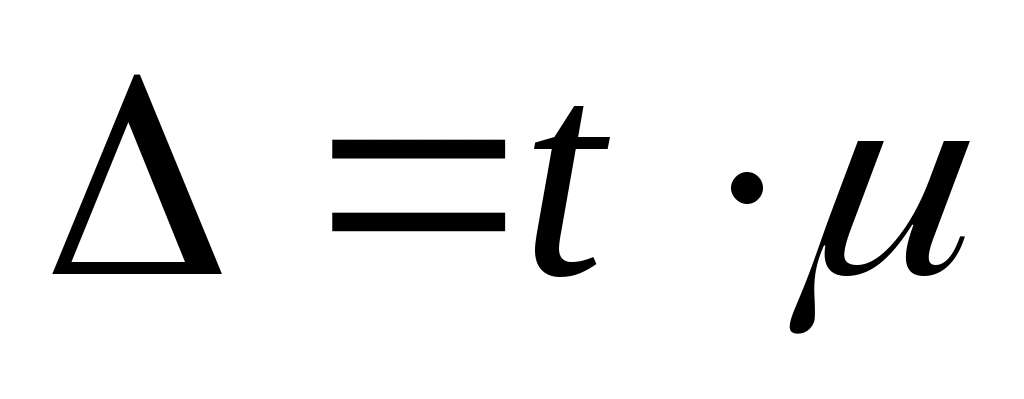где
– предельная ошибка выборки;
μ - средняя ошибка выборки;
t – коэффициент доверия.
Коэффициент доверия определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного исследования. Для определения t пользуются таблицами нормального распределения. Некоторые наиболее часто встречающиеся значения этого коэффициента приведены в таблице 9.
Таблица 9 – Уровни вероятности и соответствующие им значения коэффициента доверия
Таким образом, границы доверительного интервала могут быть представлены следующим образом:
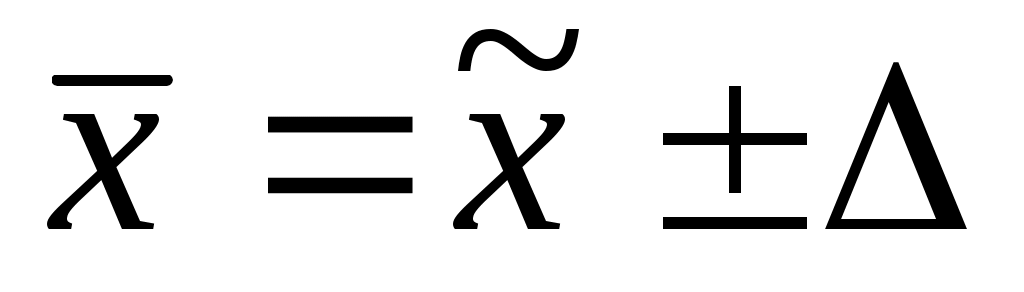или 
,
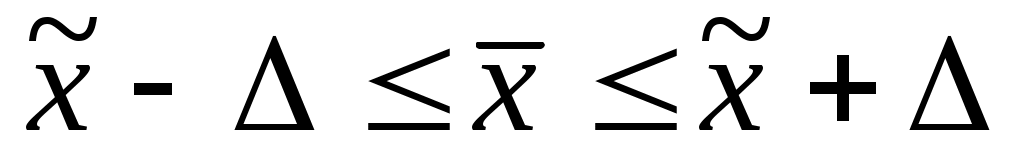В нашем примере среднюю ошибку выборки найдем по формуле:
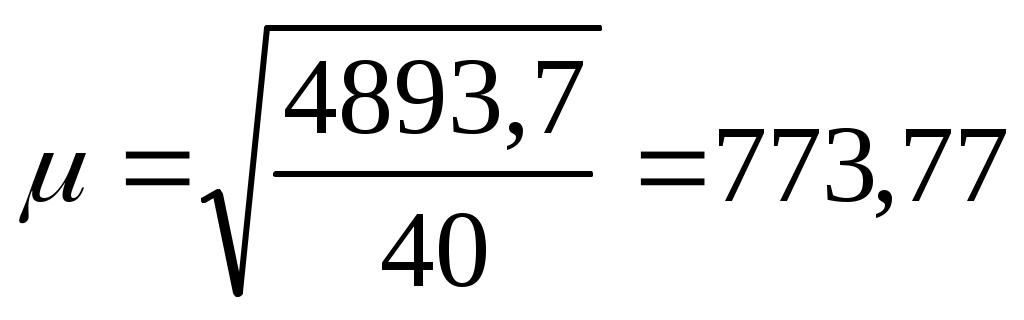руб.
Предельная ошибка выборки при вероятности Р=0,954 составит:
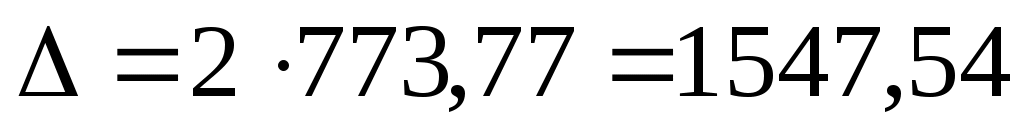руб.
Границы доверительного интервала:
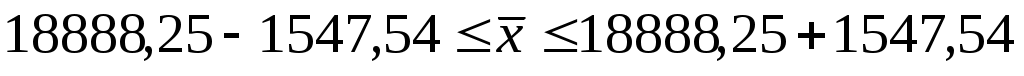
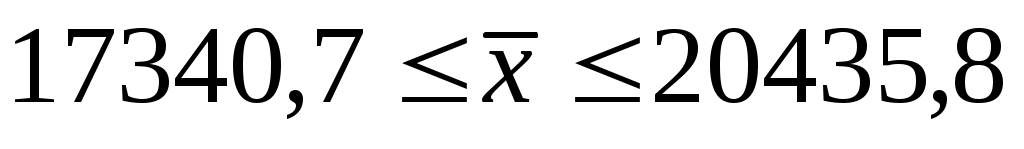
7. Произвести корреляционно-регрессионный анализ данных: описать взаимосвязь между численностью населения и валовым региональным продуктом:
а) сформировать таблицу с исходными данными: факторный признак (х) – численность населения, тыс. чел.; результативный (у) – валовый региональный продукт, млн. руб.;
б) предположить наличие линейной зависимости между рассматриваемыми признаками, рассчитать параметры парной линейной регрессии методом наименьших квадратов;
в) графически изобразить линии теоретических и фактических значений;
г) определить степень тесноты связи при помощи линейного коэффициента корреляции.
Сделайте выводы по результатам расчетов.
Исследование объективно существующих связей между явлениями – важнейшая задача статистики. Признаки по их значению для изучения взаимосвязи делятся на факторные и результативные. Факторные признаки (х) – признаки, обуславливающие изменение других, связанных с ними признаков. Результативные признаки (у)– признаки, изменяющиеся под действием факторных признаков.
Аналитически связь между признаками может быть описана уравнением прямой (парной линейной регрессии):
y = a + bx;
Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов, в соответствии с которым минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
.
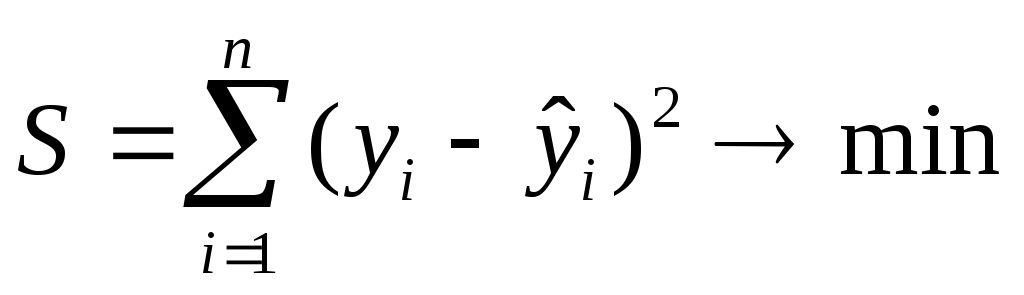Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
,
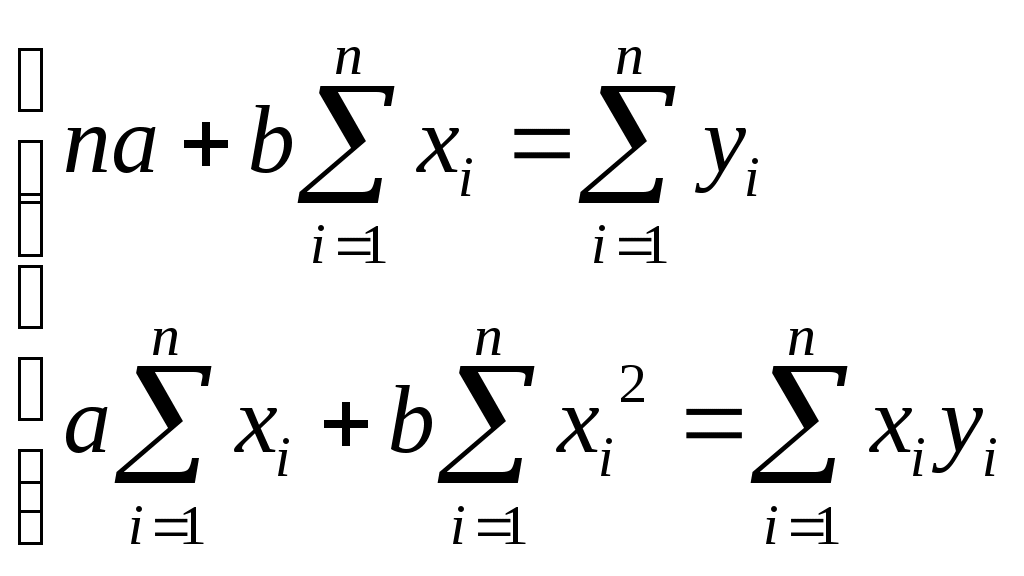где n – объем исследуемой совокупности (число единиц наблюдения).
Решая данную систему уравнений получим:
; 
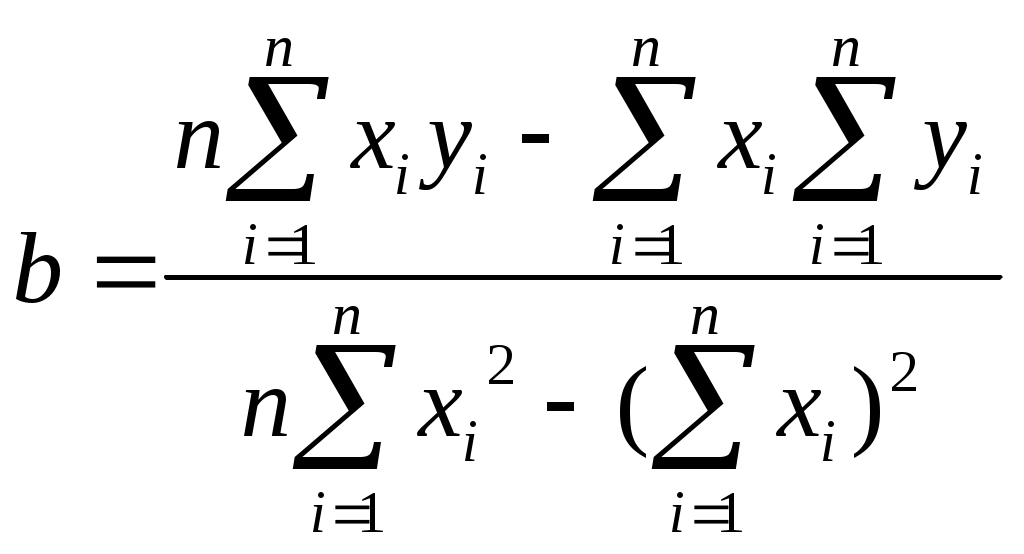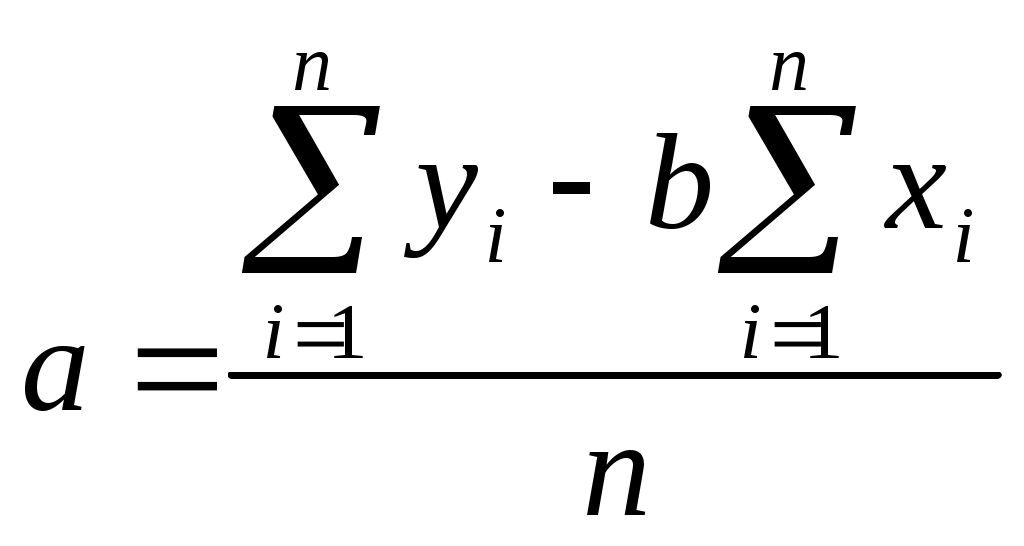
В уравнениях регрессии параметр a показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии b показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного признака на единицу собственного измерения.
Теснота связи количественно выражается величиной коэффициента корреляции, который характеризует степень линейной зависимости между двумя переменными. В статистической теории разработаны и на практике применяются различные модификации формул расчета линейного коэффициента корреляции, например:
.
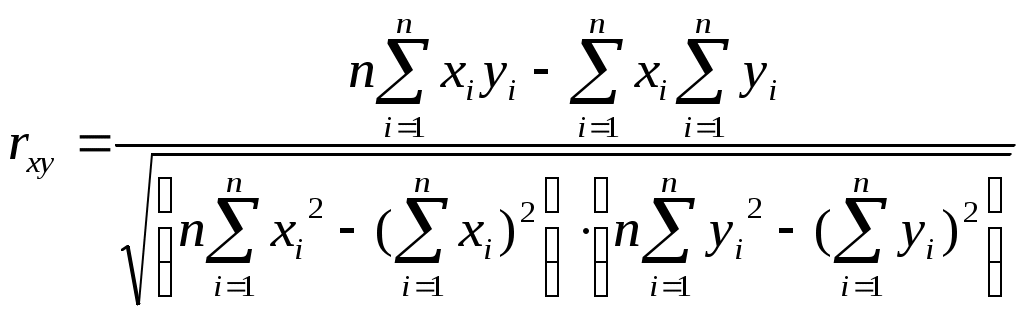Свойства коэффициента корреляции.
1) Коэффициент корреляции изменяется в пределах от –1 до +1: –1 ≤ r ≤ 1. Чем ближе |r| к единице, тем теснее связь.
2) При r = ± 1 связь между величинами линейная.
3) При r = 0 линейная связь между величинами отсутствует.
4) При r > 0 связь между величинами положительная (прямая), т.е. с увеличением (уменьшением) x соответственно увеличивается (уменьшается) y.
5) При r < 0 связь между величинами отрицательная (обратная), т.е. с увеличением x уменьшается y и наоборот.
Для расчета параметров линейного уравнения регрессии и коэффициента корреляции создадим таблицу 10.
Система нормальных уравнений для данного примера имеет вид:
.
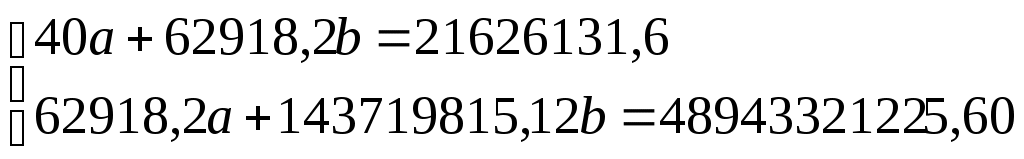Отсюда:
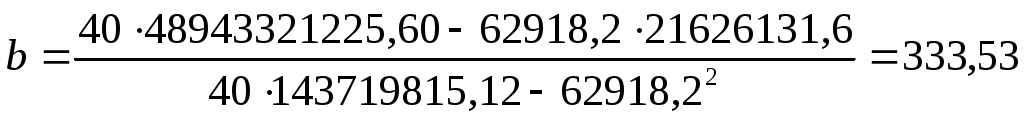
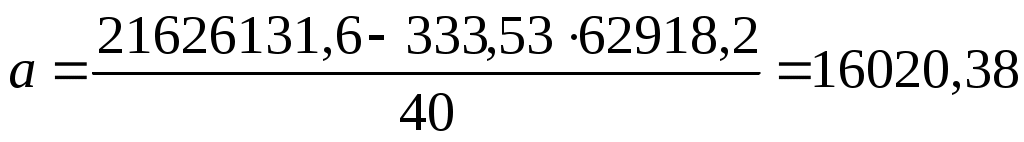
Получим уравнение прямой:
y = 16020,38 + 333,53x
Рассчитаем по полученному уравнению прямой теоретические значения валового регионального продукта. Теоретические и фактические значения валового регионального продукта представлены на рисунке 8.
Коэффициент корреляции:
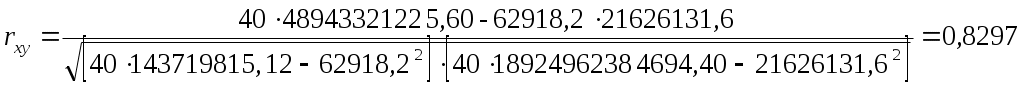
Таблица 10 – Данные для корреляционно-регрессионного анализа
Коэффициент вариации:
или 25,91%
6. Определить с доверительной вероятностью 0,954 возможные пределы колебаний средней величины группировочного признака в генеральной совокупности.
Выборочное наблюдение – несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.
Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей. Генеральная совокупность – исходная изучаемая статистическая совокупность, из которой производится отбор части единиц. Выборочная совокупность (выборка) – отобранная из генеральной совокупности некоторая часть единиц, подвергающаяся обследованию.
Отбор единиц в выборочную совокупность может быть:
1) повторным;
2) бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора.
При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует, т.е. не возвращается обратно.
Средняя ошибка выборки определяется по следующим формулам:
а) при повторном отборе
,где μ – средняя ошибка выборки;
– дисперсия выборочной совокупности;n – объем (число единиц) выборочной совокупности;
б) при бесповторном отборе:
,где N – число единиц в генеральной совокупности.
При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности
, с которым гарантируется, что генеральная средняя не выйдет за указанные границы:
,где
– предельная ошибка выборки;μ - средняя ошибка выборки;
t – коэффициент доверия.
Коэффициент доверия определяется в зависимости от того, с какой доверительной вероятностью надо гарантировать результаты выборочного исследования. Для определения t пользуются таблицами нормального распределения. Некоторые наиболее часто встречающиеся значения этого коэффициента приведены в таблице 9.
Таблица 9 – Уровни вероятности и соответствующие им значения коэффициента доверия
| Доверительная вероятность (P) | 0,683 | 0,950 | 0,954 | 0,997 |
| Коэффициент доверия (t) | 1,00 | 1,96 | 2,00 | 3,00 |
Таким образом, границы доверительного интервала могут быть представлены следующим образом:
или ,В нашем примере среднюю ошибку выборки найдем по формуле:
руб.Предельная ошибка выборки при вероятности Р=0,954 составит:
руб.Границы доверительного интервала:
7. Произвести корреляционно-регрессионный анализ данных: описать взаимосвязь между численностью населения и валовым региональным продуктом:
а) сформировать таблицу с исходными данными: факторный признак (х) – численность населения, тыс. чел.; результативный (у) – валовый региональный продукт, млн. руб.;
б) предположить наличие линейной зависимости между рассматриваемыми признаками, рассчитать параметры парной линейной регрессии методом наименьших квадратов;
в) графически изобразить линии теоретических и фактических значений;
г) определить степень тесноты связи при помощи линейного коэффициента корреляции.
Сделайте выводы по результатам расчетов.
Исследование объективно существующих связей между явлениями – важнейшая задача статистики. Признаки по их значению для изучения взаимосвязи делятся на факторные и результативные. Факторные признаки (х) – признаки, обуславливающие изменение других, связанных с ними признаков. Результативные признаки (у)– признаки, изменяющиеся под действием факторных признаков.
Аналитически связь между признаками может быть описана уравнением прямой (парной линейной регрессии):
y = a + bx;
Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов, в соответствии с которым минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
.Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
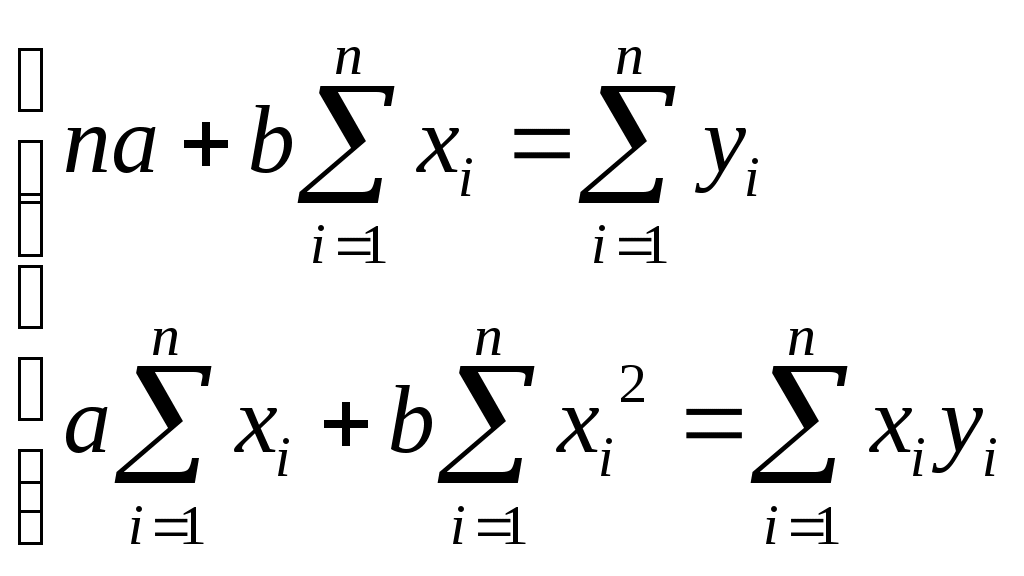,где n – объем исследуемой совокупности (число единиц наблюдения).
Решая данную систему уравнений получим:
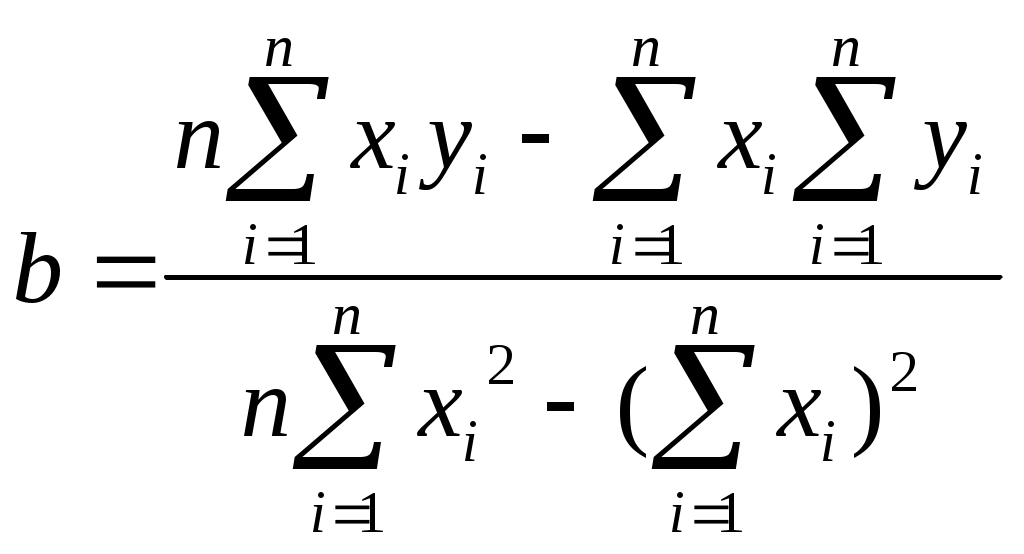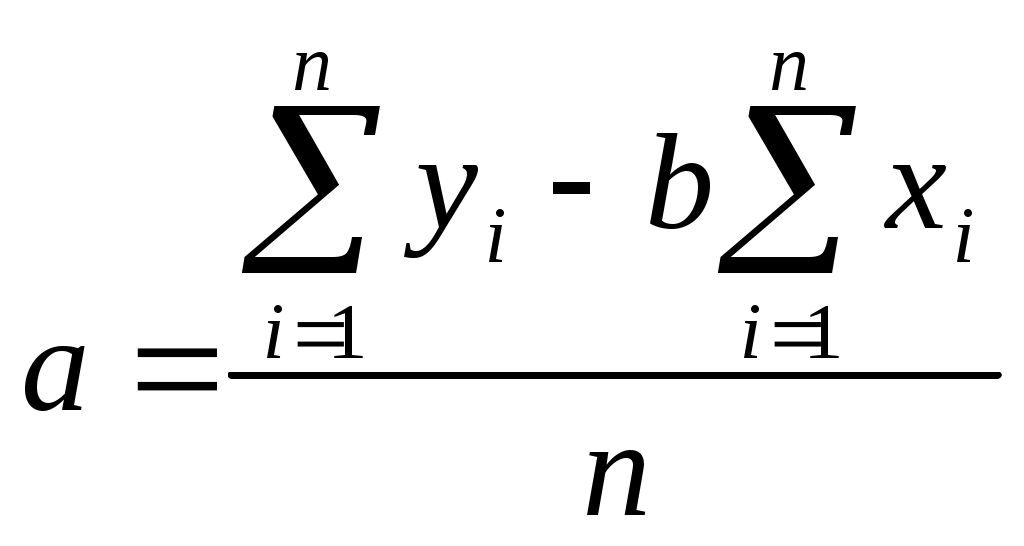
; В уравнениях регрессии параметр a показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии b показывает, на сколько в среднем изменяется значение результативного признака при увеличении факторного признака на единицу собственного измерения.
Теснота связи количественно выражается величиной коэффициента корреляции, который характеризует степень линейной зависимости между двумя переменными. В статистической теории разработаны и на практике применяются различные модификации формул расчета линейного коэффициента корреляции, например:
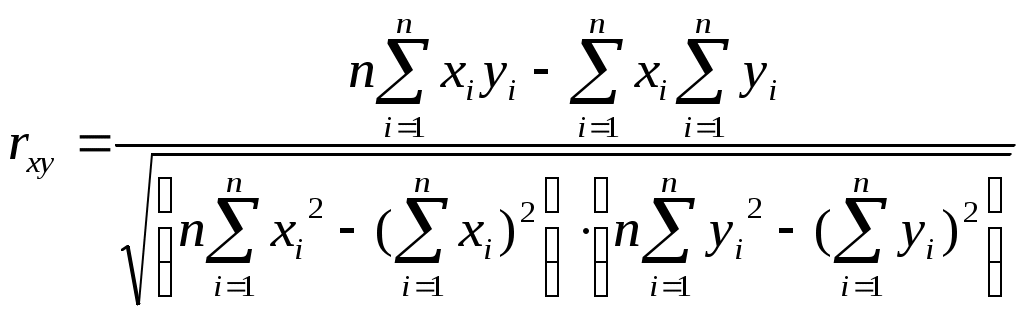.Свойства коэффициента корреляции.
1) Коэффициент корреляции изменяется в пределах от –1 до +1: –1 ≤ r ≤ 1. Чем ближе |r| к единице, тем теснее связь.
2) При r = ± 1 связь между величинами линейная.
3) При r = 0 линейная связь между величинами отсутствует.
4) При r > 0 связь между величинами положительная (прямая), т.е. с увеличением (уменьшением) x соответственно увеличивается (уменьшается) y.
5) При r < 0 связь между величинами отрицательная (обратная), т.е. с увеличением x уменьшается y и наоборот.
Для расчета параметров линейного уравнения регрессии и коэффициента корреляции создадим таблицу 10.
Система нормальных уравнений для данного примера имеет вид:
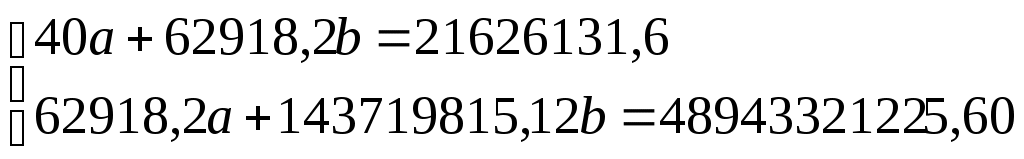.Отсюда:
Получим уравнение прямой:
y = 16020,38 + 333,53x
Рассчитаем по полученному уравнению прямой теоретические значения валового регионального продукта. Теоретические и фактические значения валового регионального продукта представлены на рисунке 8.
Коэффициент корреляции:
Таблица 10 – Данные для корреляционно-регрессионного анализа
| № | Субъекты РФ | Численность населения на 1 января населения 2017 г., тыс. человек, xi | Валовой региональный продукт в 2015 г., млн. руб., yi | xi2 | xiyi | y=-859346,72+988,68x | yi2 |
| 1 | Республика Ингушетия | 480,5 | 54330,4 | 230880,25 | 26105757,20 | 176283,14 | 2951792364,16 |
| 2 | Республика Калмыкия | 277,8 | 47291,7 | 77172,84 | 13137634,26 | 108675,94 | 2236504888,89 |
| 3 | Чеченская Республика | 1414,9 | 160503,2 | 2001942,01 | 227095977,68 | 487936,68 | 25761277210,24 |
| 4 | Республика Марий Эл | 684,7 | 165531,0 | 468814,09 | 113339075,70 | 244390,65 | 27400511961,00 |
| 5 | Курганская область | 854,1 | 179711,8 | 729486,81 | 153491848,38 | 300891,19 | 32296331059,24 |
| … | |||||||
| 35 | Республика Дагестан | 3041,9 | 559673,1 | 9253155,61 | 1702469602,89 | 1030595,40 | 313233978863,61 |
| 36 | Республика Татарстан | 3885,2 | 1833214,5 | 15094779,04 | 7122404975,40 | 1311864,05 | 3360675403010,25 |
| 37 | Мурманская область | 757,6 | 390390,0 | 573957,76 | 295759464,00 | 268705,23 | 152404352100,00 |
| 38 | Республика Саха (Якутия) | 962,8 | 749987,5 | 926983,84 | 722087965,00 | 337146,26 | 562481250156,25 |
| 39 | Магаданская область | 145,6 | 124596,9 | 21199,36 | 18141308,64 | 64582,83 | 15524387489,61 |
| 40 | Сахалинская область | 487,4 | 829298,6 | 237558,76 | 404200137,64 | 178584,52 | 687736167961,96 |
| Итого | 62918,2 | 21626131,6 | 143719815,12 | 48943321225,60 | 21626131,60 | 18924962384694,40 | |