Файл: Цель практической работы 2 Теоретическое введение 2.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Оглавление
Цель практической работы 2
Теоретическое введение 2
Задание 1 7
Задание 2 7
Вывод 11
Цель практической работы
Исследовать сети Петри и временные сети Петри. Симулировать работу сетей Петри на примере работы автоматизированного станка и параллельной работы трёх таких станков.
Теоретическое введение
Сети Петри представляют собой простое и удобное средство для моделирования разнообразных распределенных систем и процессов. Эта модель была придумана немецким ученым Карлом Петри в 1939 году для описания химических процессов. Официальная история сетей Петри началась в 1962 году, когда Карл Петри защитил диссертацию
0.1 Классические сети Петри
0.1.1 Понятие сети Петри
Сеть Петри представляет собой двудольный ориентированный граф, содержащий вершины двух типов - места (обозначаются кружками) и переходы (обозначаются прямоугольниками). Любая дуга ведет либо от вершины–места в вершину–переход, либо наоборот. Дуги, соединяющие два места или два перехода, запрещены. Места, у которые нет входящих дуг, называются входными. Места, у которых нет исходящих дуг, называются выходными.
Каждое место сети Петри может содержать ноль или более меток (маркеров, англ. tokens). Все метки считаются одинаковыми и неотличимыми друг от друга. Распределение меток по местам сети называется ее разметкой. Работа сети начинается с начальной разметки.
Метки могут переноситься с одного места на другое. Перенос меток выполняется по следующей схеме.
Переход является активным, если каждое его входное место содержит по крайней мере одну метку (более точно - по одной метке на каждую входящую в этот переход дугу).
Активный переход может сработать, при срабатывании переход поглощает по одной метке с каждого своего входного места и размещает по одной метке на каждое свое выходное место (по одной метке на каждую исходящую дугу).
В каждый момент времени для срабатывания из всех активных переходов недетерминированным образом выбирается один. Если активных переходов нет, то работа сети на этом завершается.
Припишем каждому переходу сети Петри некоторый уникальный символ (например, пронумеруем их). Последовательность символов σ, в которой i-ый символ равен символу перехода, сработавшему на i-ом шаге
работы сети, называется последовательностью срабатываний сети Петри. Последовательность срабатываний однозначно определяет последовательность разметок µi, где µ0 является начальной разметкой. Тот факт, что после срабатывания t-го перехода разметка µ преобразуется в разметку µl, будем обозначать кратко µ →t µl.
На рисунке 0.1 показан пример работы сети Петри для последователь ности срабатываний σ = [t1, t3]. Активные переходы в каждом случае по- мечены звездочкой. Заметим, что для той же сети имеется еще только одна возможная последовательность срабатываний σ = [t1, t2].
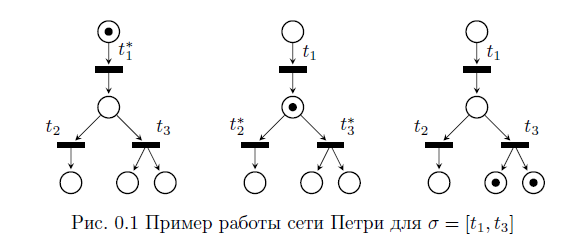
На рисунке 0.2 приведен пример моделирования сетью Петри простого светофора, в котором цвета переключаются в следующем порядке (зеленый, желтый, красный), причем продолжительность каждого сигнала одинакова (и равна одному такту работы сети Петри). Особенностью этой сети является то, что ее работа никогда не завершается.
0.1.3 Свойства сетей Петри
Отдельные элементы сети Петри (места и переходы) могут обладать различными свойствами, на основе которых сначала определяются свойства самих сетей, а затем строится и их классификация.
Простейшим свойством места является количество меток, которые могут в нем располагаться. Если в любой достижимой разметке число меток в заданном месте будет не более одной (0 или 1), то такое место называется безопасным. Сеть Петри называется безопасной, если все ее места безопасны. В безопасных сетях состояние каждого места описывается всего одним битом, поэтому такие сети могут быть легко реализованы аппаратно, используя те или иные виды переключателей (триггеров). Кстати, первоначальный вариант определения сети Петри, данный самим Адамом Петри, как раз подразумевал, что сеть является безопасной.
Однако, для большинства приложений требование безопасности сети является чересчур строгим. Его можно ослабить, разрешив каждому месту хранить некоторое ограниченное число меток. Более строго, место называется k-ограниченным, если в любой достижимой разметке в данном месте будет не более k меток. Очевидно, что 1-ограниченное место является безопасным. Место называется ограниченным, если существует такое k, что это место является k-ограниченным. Наконец, сеть Петри является k-ограниченной, если любое его место является k-ограниченным, и просто ограниченной, если все его места ограничены. Ограниченные сети также допускают эффективную аппаратную реализацию, в которой каждое место представляется уже счетчиком (например, регистром) некоторой заданной емкости. Неограниченные сети имеют, как правило, только теоретический интерес.
Еще одним свойством сетей Петри, основанным на подсчете числа меток, является свойство консервативности. Сеть называется консервативной, если число меток в любой достижимой разметке сохраняется одним и тем же (равным числу меток в начальной разметке). Такая модель используется, например, в тех случаях, когда метки представляют собой некоторые ресурсы системы, которые не уничтожаются и не создаются. Эти ресурсы могут переходить от одной части системы к другой, но их суммарное количество в процессе работы системы не изменяется. Нетрудно показать, что любой переход, который встречается хотя бы в одной достижимой разметке, дол- жен иметь одинаковое число входных и выходных дуг - сколько он выбрал меток, столько он должен их и поставить.
0.2 Параллельные процессы
В стандартной интерпретации сетей Петри каждый переход трактуется как некоторый процесс, который берет свои входные данные из входных мест, обрабатывает их некоторым образом и помещает результат в свои выходные места. Однако, природа эти процессов, в частности, их продолжительность, никак не конкретизируется. Хотя сети Петри обладают необходимым потенциалом для моделирования параллельно происходящих процессов, очевидно, что говорить о параллельности процессов имеет смысл только тогда, когда они имеют некую продолжительность.
0.2.1 Последовательная обработка процессов
В простейшем варианте сеть Петри может рассматриваться как последовательное устройство, работа которого заключается в реализации некоторой последовательности срабатываний. Такая интерпретация имеет смысл в нескольких случаях. Например, если в модели предполагается непрерывное время, а продолжительность срабатывания перехода является нулевой, то вероятность одновременного срабатывания двух переходов может считаться равной нулю. Очевидно, что в этом случае, важным оказывается как раз порядок (последовательность) срабатывания переходов.
Последовательностная интерпретация работы сети Петри применяется также в тех случаях, когда все процессы (переходы) обрабатываются одним и тем же устройством (исполнителем). Примером такого рода системы может служить однопроцессорный компьютер, в котором выполняется сразу несколько различных процессов. Эти процессы логически могут быть не связанными друг с другом (и рассматриваться пользователем как параллельные), однако, реализуются эти процессы в системе строго последовательно один за другим.
0.2.2 Параллельная обработка процессов
Более адекватной во многих случаях являются интерпретации сетей Петри, в которых процессы могут обрабатываться одновременно. В стандартной модели такой сети предполагается, что время срабатывания всех переходов является одинаковым. Для простоты будем считать, что это время равно единице. Также положим, что срабатывание любого перехода производится в целочисленный момент времени. Таким образом, время в модели оказывается дискретным, его отсчет будем вести с нулевого момента (начальная разметка).
Для того, чтобы описать параллельное поведение сети Петри, необходимо определить понятие конфликта. Конфликтом в сети Петри называется ситуация, когда сразу несколько активных переходов претендуют на одну метку некоторого места. При последовательном срабатывании переходов конфликты никак не учитываются, однако при параллельной интерпретации требуется некоторый способ их разрешения. Пример конфликта показан на рисунке 0.4, на котором переходы t1 и t2 конфликтуют из-за общей метки в месте p.
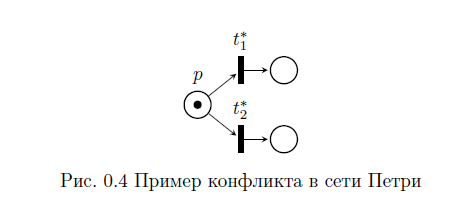
Стандартная схема параллельной обработки переходов в сетях Петри выглядит следующим образом: из всех активных в данный момент времени переходов выбирается некоторое их бесконфликтное подмножество (никакие два из выбранных переходов не имеют взаимного конфликта); все эти переходы срабатывают одновременно. Как и выше, если активных переходов нет, то сеть завершает свою работу.
0.3.4 Временные сети Петри
Для моделирования систем, в которых отдельные подпроцессы имеют различную продолжительность, можно использовать временные сети Петри. В таких сетях каждая метка получает дополнительный атрибут - время задержки. Если метка появилась в каком-то месте в момент времени t и имеет время задержки τ , то она будет доступна для всех переходов (связанных с данным местом) начиная с момента времени t + τ .
Задержки, которые назначаются меткам, приписываются дугам, ведущим от переходов. Соответственно, все метки, поставляемые по какой-либо дуге, будут получать одну и ту же задержку, которая приписана этой дуге. По умолчанию считается, что задержка каждой дуги является единичной.
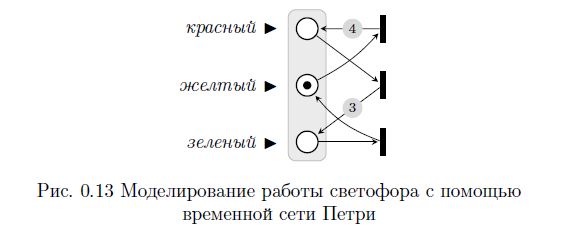
На рисунке 0.13 приведен пример моделирования с помощью временной сети Петри светофора, у которого продолжительность красного сигнала равна четырем тактам, желтого - одному такту (значение по умолчанию), зеленого - трем тактам.
Задание 1
Реализовал модель работы станка, используя программные комплекс PIPE2 (рисунок 1), и провел моделирование его работы в этом же комплексе. На реализацию поставленной задачи при исходной маркировке потребовалось 40 тактов сети Петри, при этом задержки внутри переходов сети Петри не учитываются, поскольку не являются частью механизма срабатывания и не приводят к рассинхронизации переходов (процесс идёт по одной линии). Для просмотра анимации смоделированной сети, откройте html версию документа.
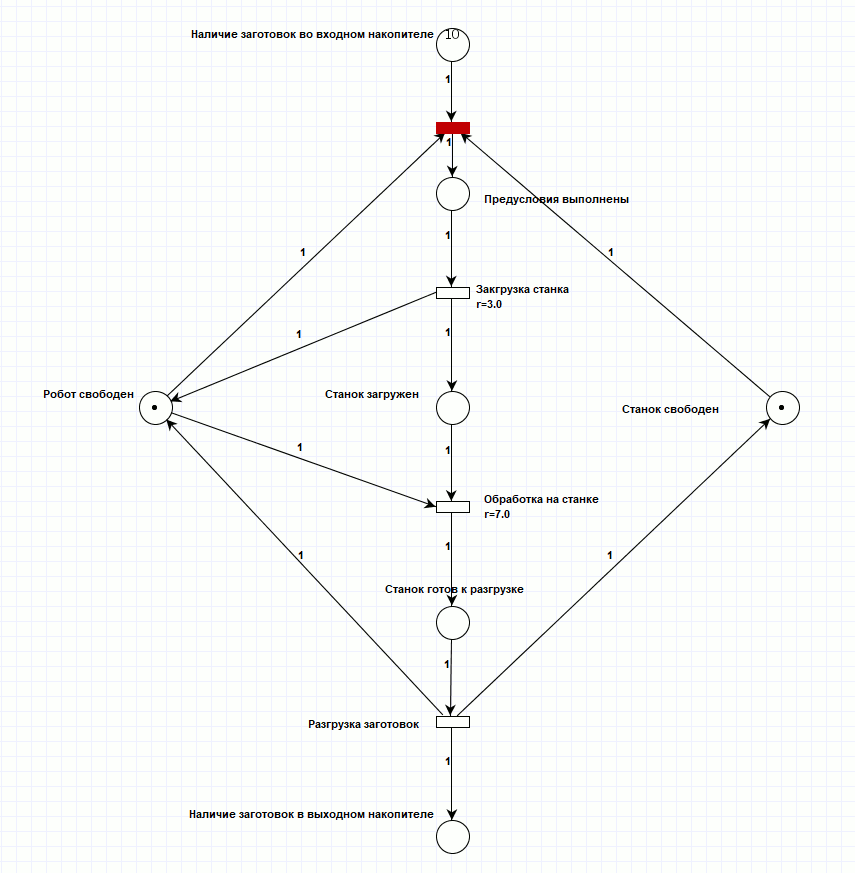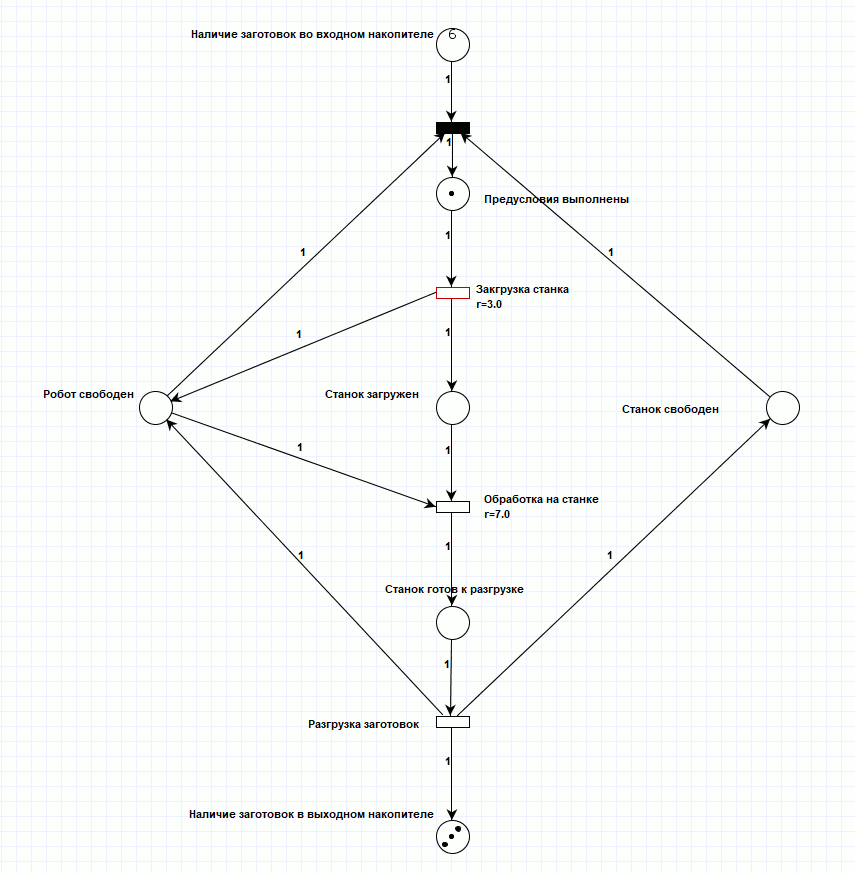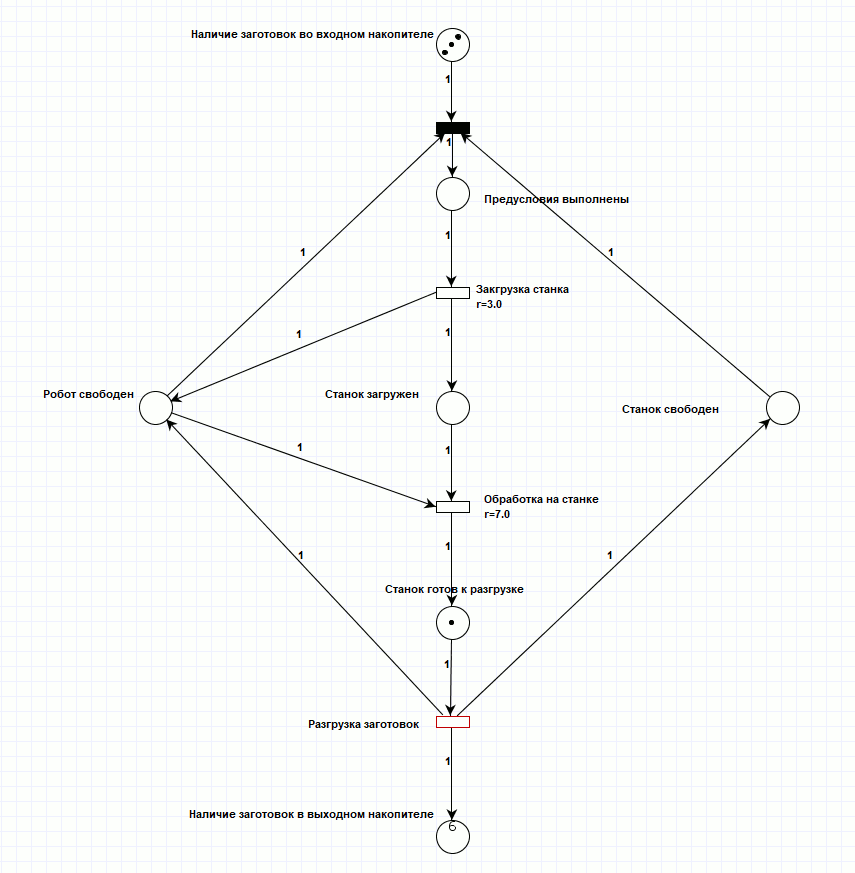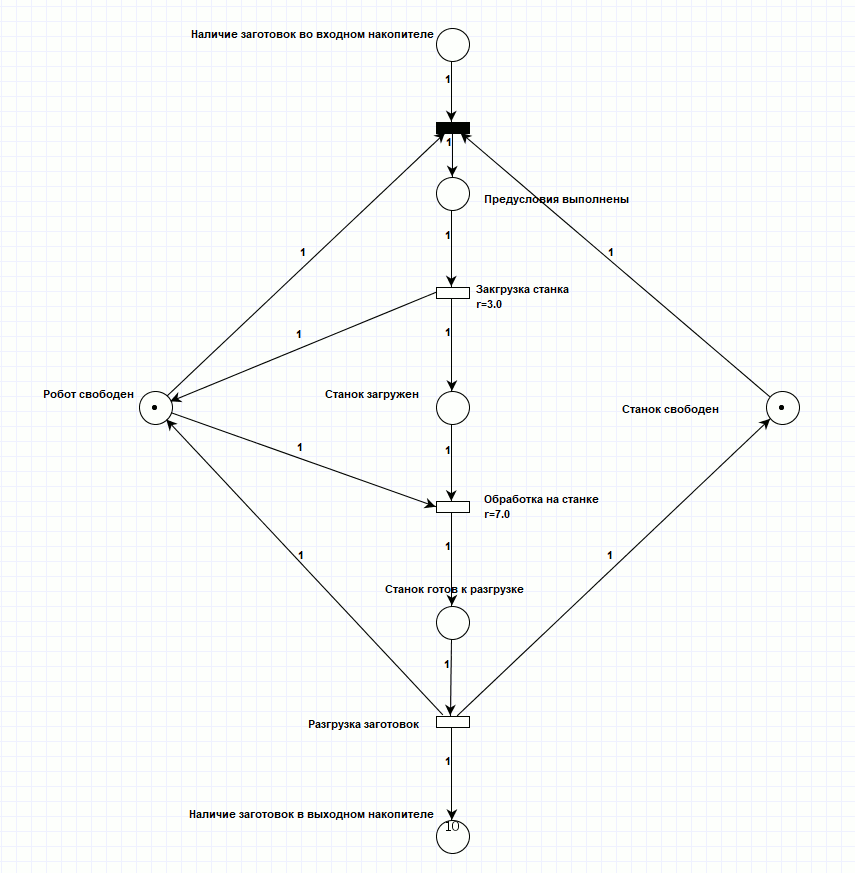
Рисунок 1. Сеть Петри производственного процесса.
Задание 2
Произвёл постепенное распараллеливание процесса на три производственные линии, в первом варианте (рисунок 2), три производственные линии были синхронизированы на входе и выходе, при этом, имеется три входных и выходных накопителя, то есть, для обрабатываемых деталей выполняется условие консервативности сети Петри (их количество не изменяется по ходу производственного процесса). Однако, как видно из анимации (для просмотра, откройте html версию документа), работа сети Петри, симулирующая работу трёх параллельных станков не синхронна, так как за раз срабатывает только один недетерминированный переход, синхронизация трёх линий происходит только на входе и выходе. Работа при заданной изначальной маркировке заняла 40 тактов.
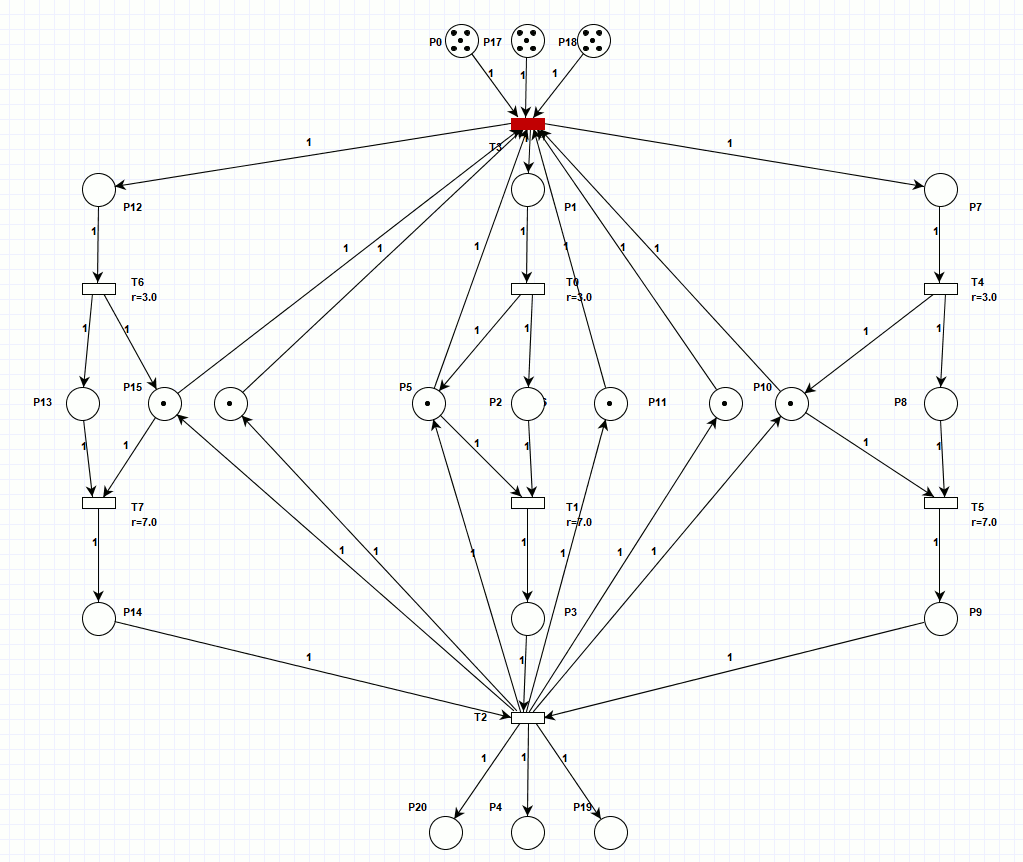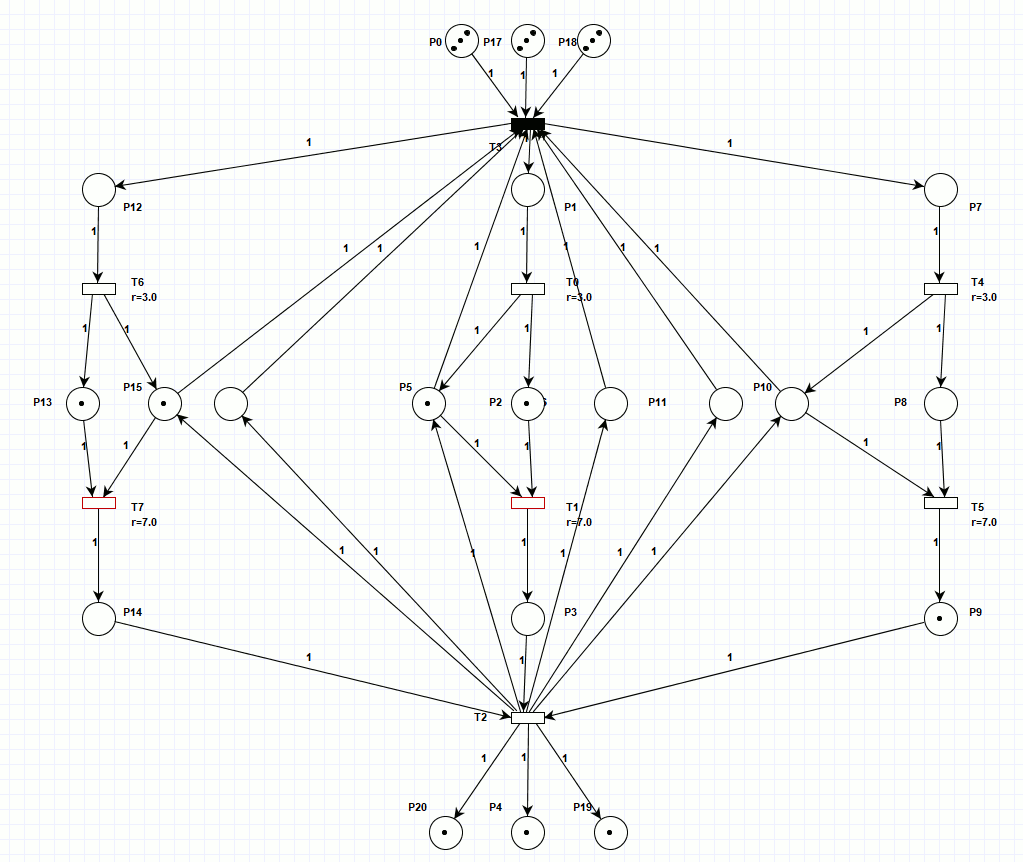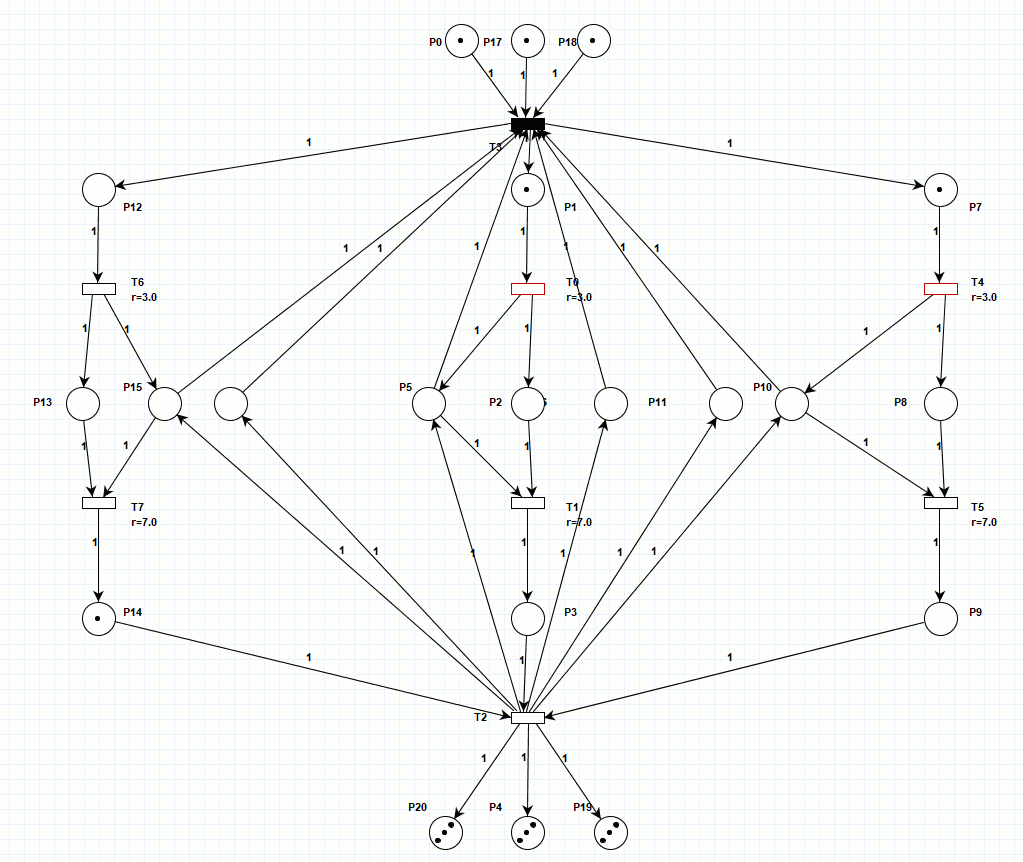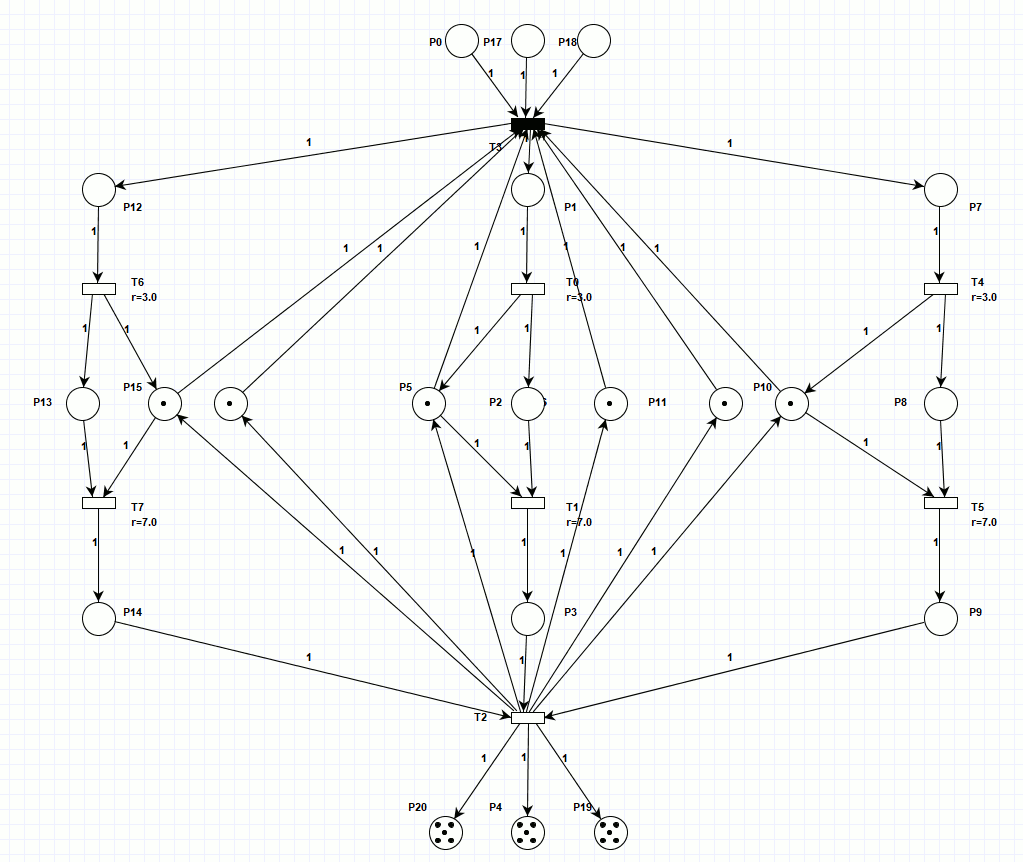
Рисунок 2. Сеть Петри для трёх линий производства.
Ниже представлена сеть Петри (рисунок 3), моделирующая тот же процесс, но действия всех трёх линий синхронизированы на каждой операции (для просмотра анимации откройте html версию документа). Однако, относительно обрабатываемых деталей, она неконсервативная, то есть количество обрабатываемых деталей в течение процесса изменяется, хотя на входе и выходе их количество остаётся неизменным. Зато работа сети при заданных начальных условиях заняла всего 20 тактов, что много меньше предыдущего результата.
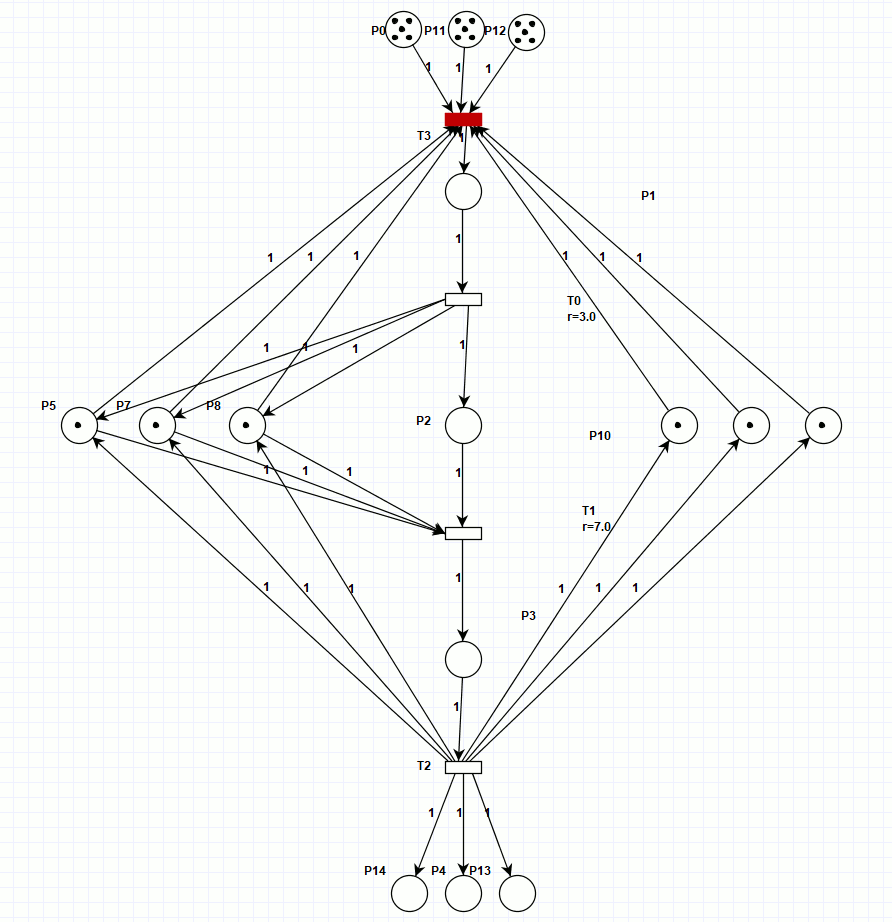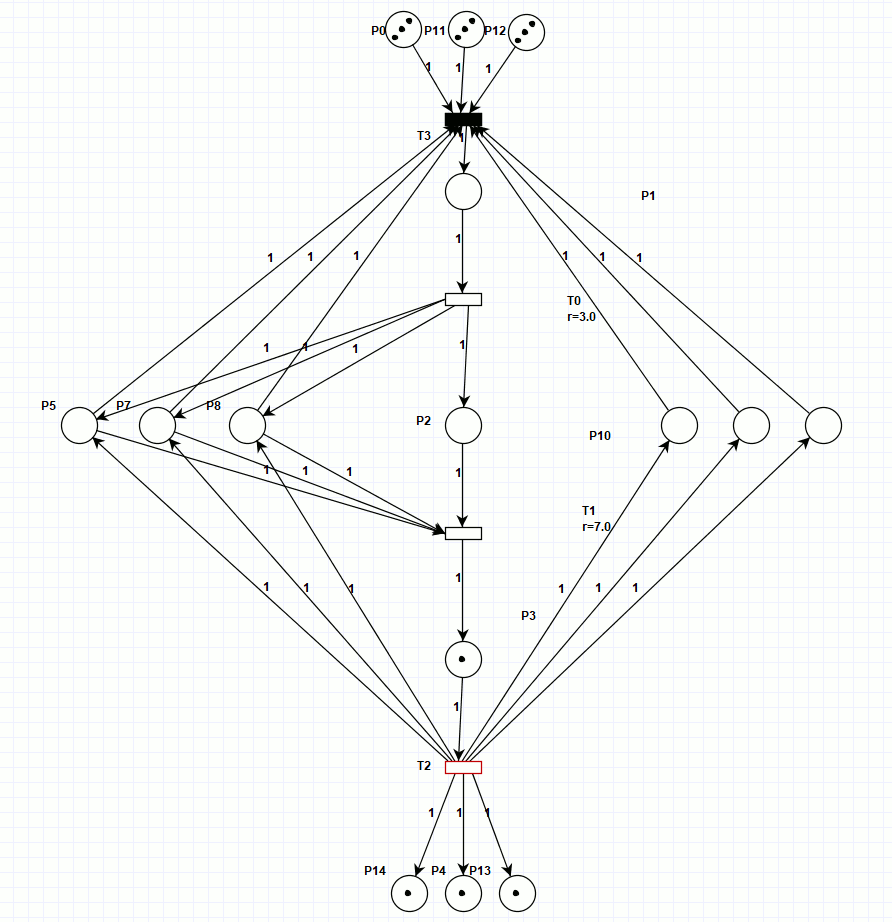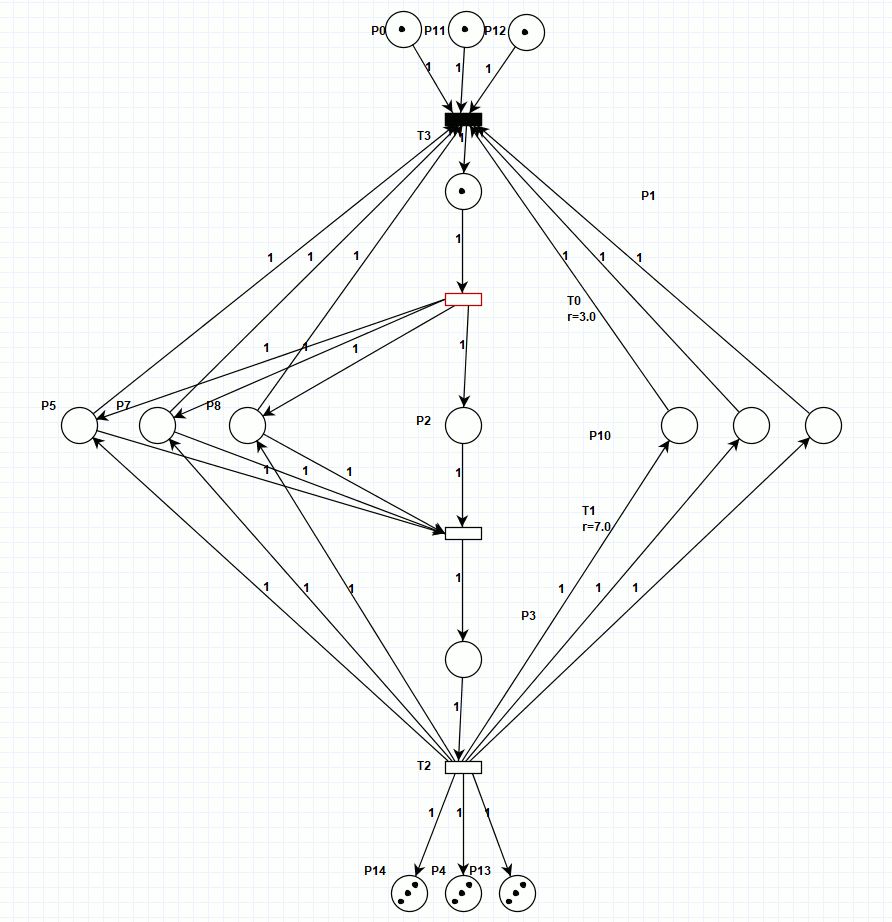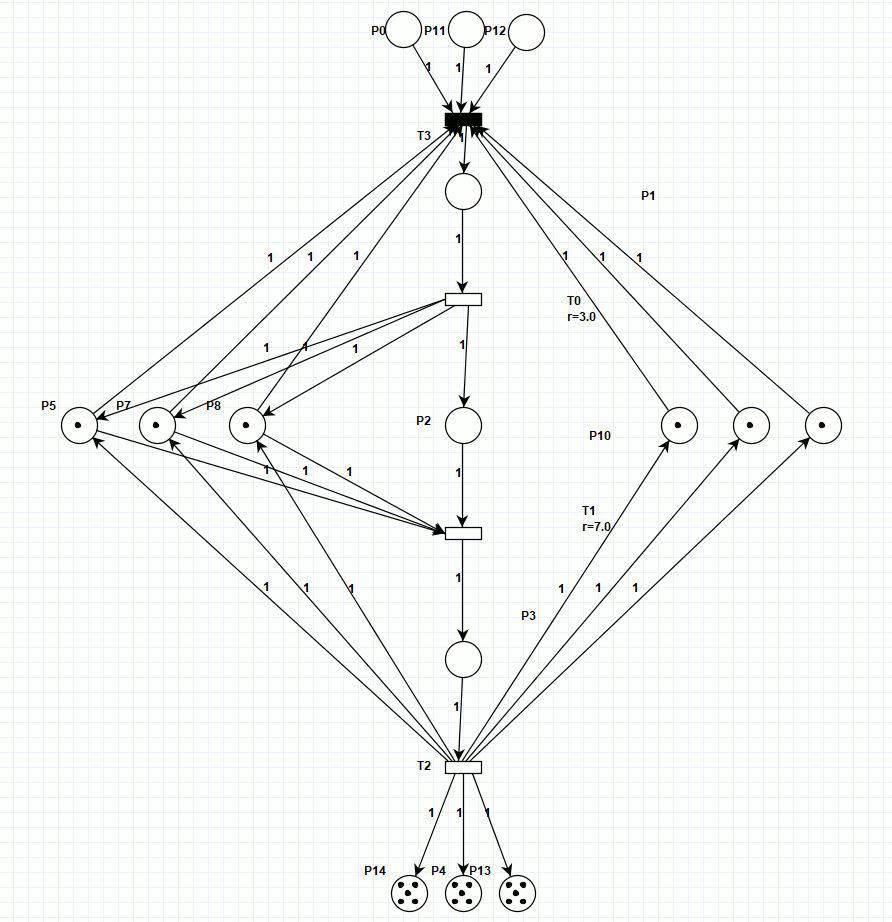
Рисунок 3. Сеть Петри, синхронизированного процесса.
Ниже представлена сеть Петри (рисунок 4), в которой, маркеры занятости роботов и станков отделены от маркеров деталей, при этом, для того, чтобы не перегружать график, места загрузки станков и роботов, отражены по одному месту на три робота или станка. Эта сеть консервативна по отношению к обрабатываемым деталям и неконсервативная по отношению к маркерам загрузки станков и роботов, но так как это не физические объекты, то было произведено такое допущение с целью не загромождать график излишними элементами. Работа этой сети занимает также 20 тактов (для просмотра анимации откройте html версию документа).
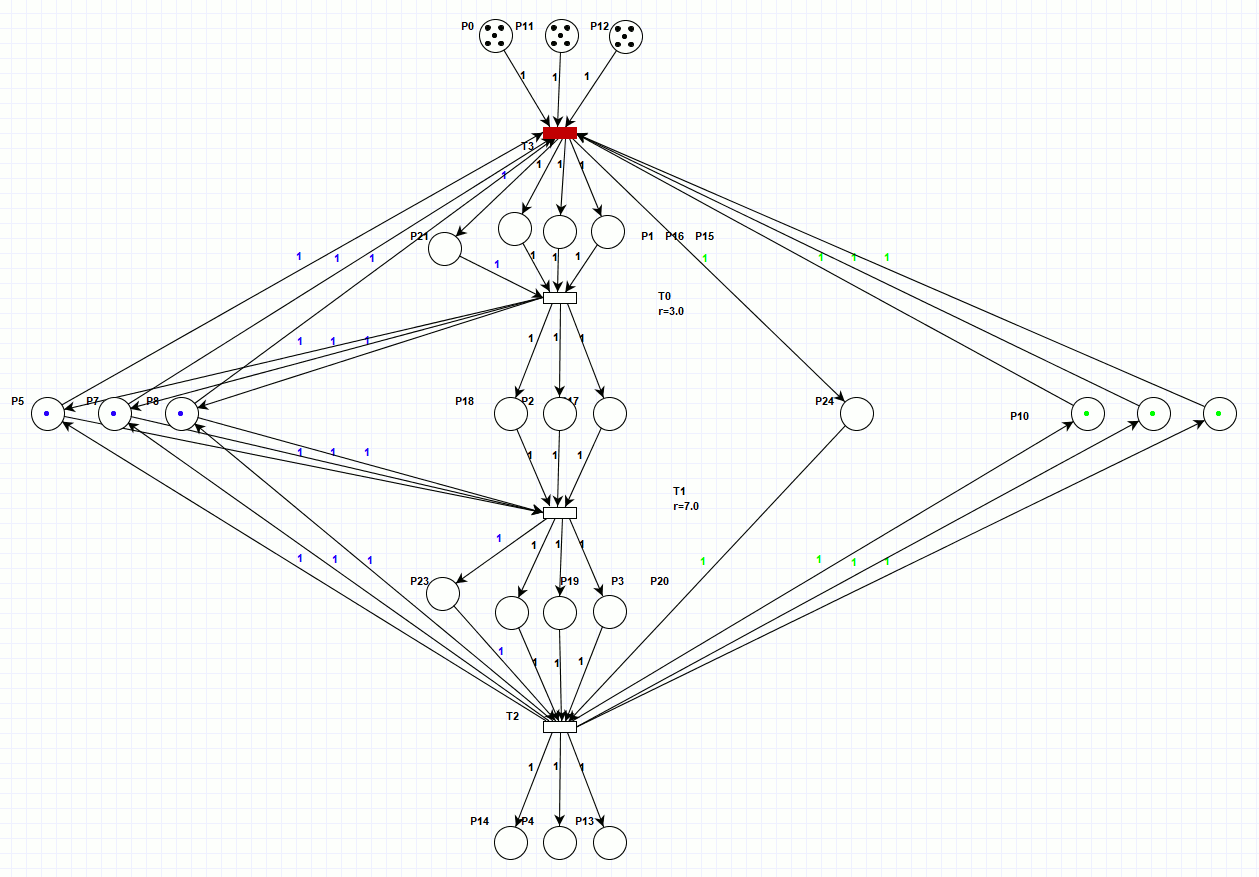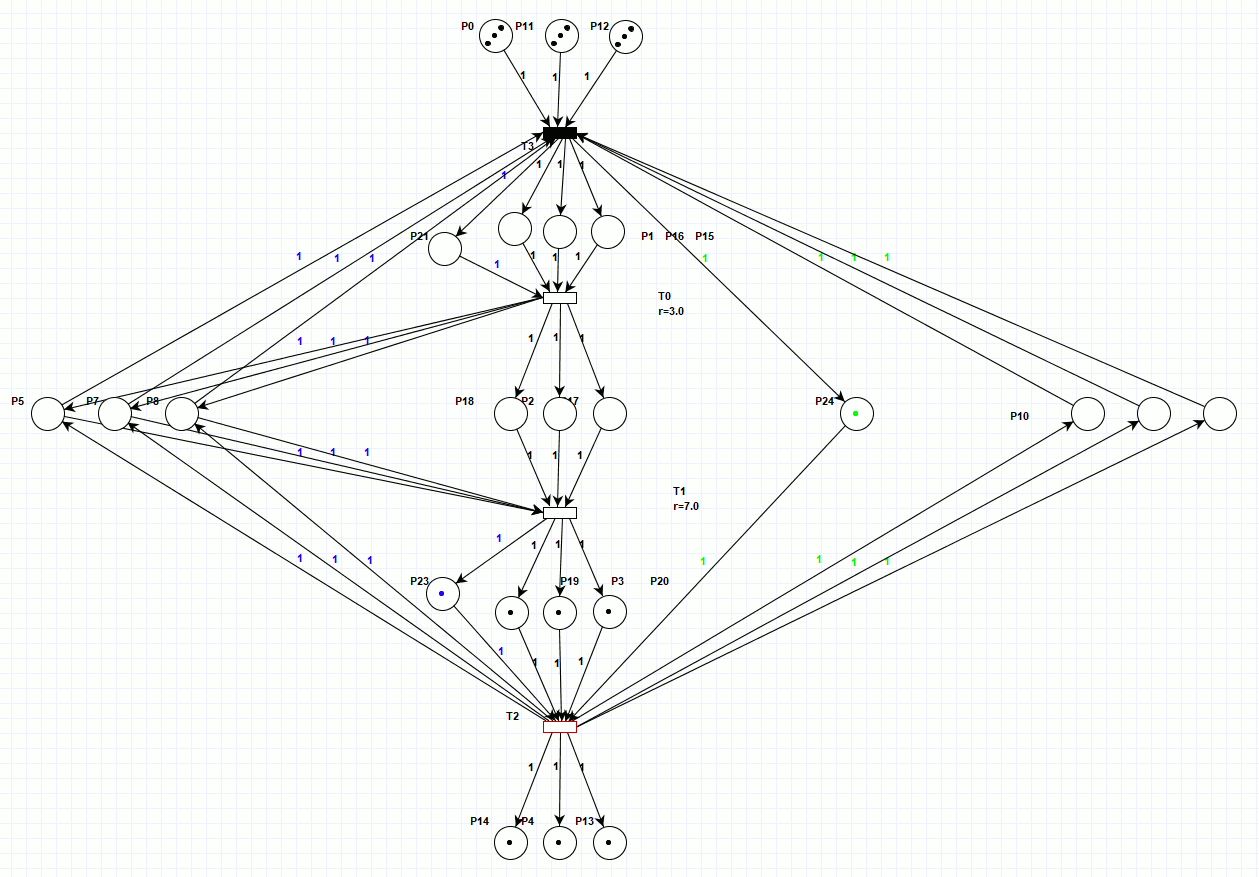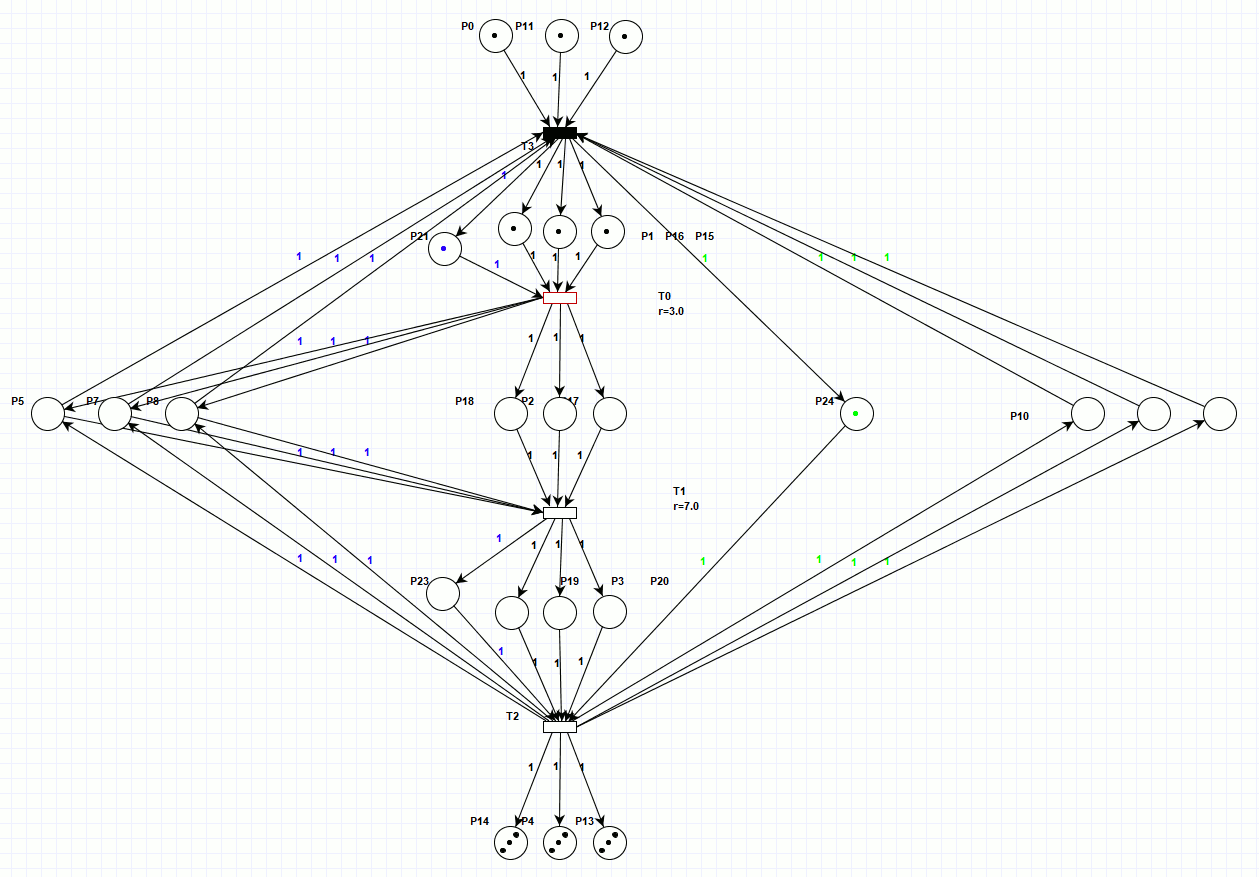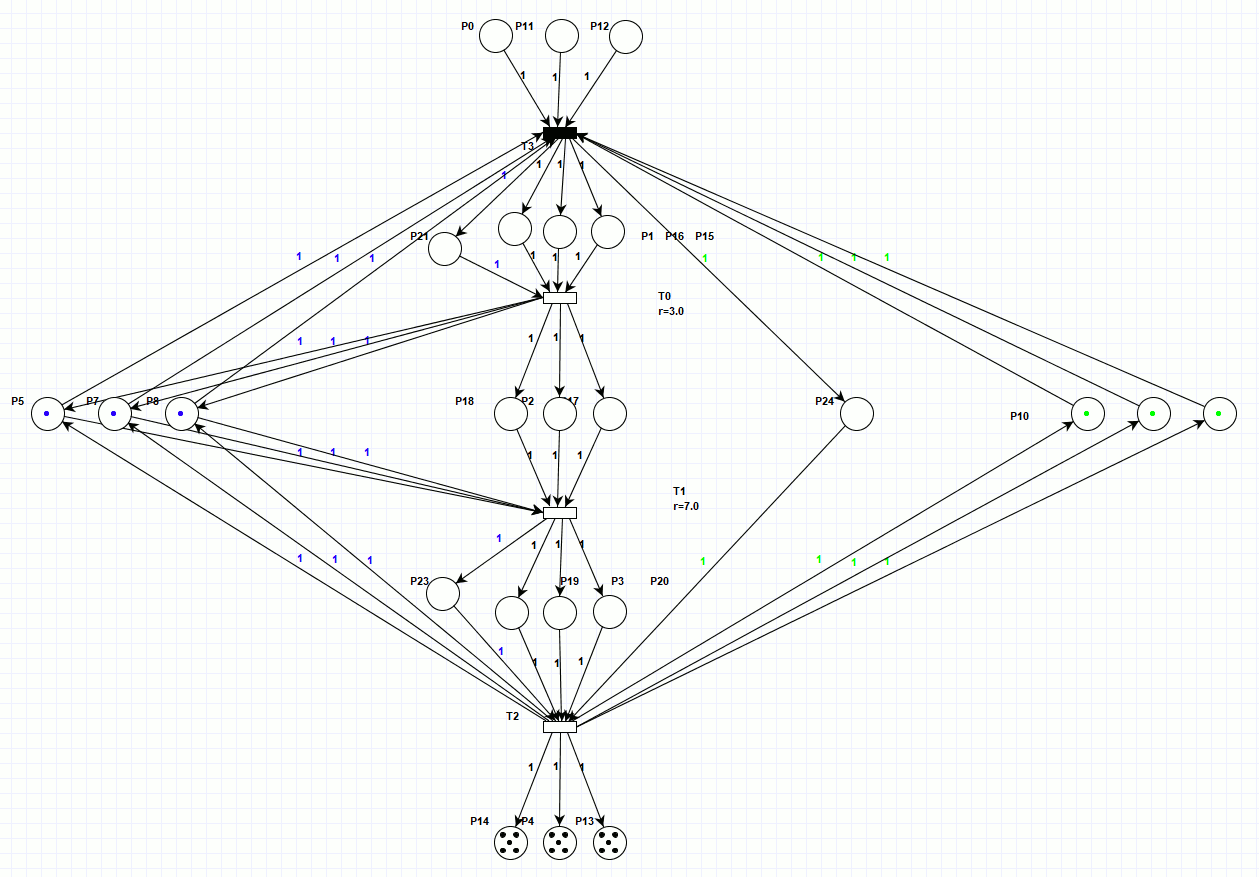
Рисунок 4. Сеть Петри параллельного процесса, консервативная по отношению к обрабатываемым деталям.
Вывод
Исследовал сети Петри и временные сети Петри. Симулировал работу сетей Петри на примере работы автоматизированного станка и параллельной работы трёх таких станков.