Добавлен: 22.11.2023
Просмотров: 148
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Государственное бюджетное профессиональное образовательное
учреждение Воронежской области
«Воронежский индустриальный колледж»
Индивидуальный проект по математике:
Тема «Математические софизмы»
Автор: Сапрыкин Давид Русланович,
студент группы ТО-221
Проверил: Попова Марина Алексеевна,
преподаватель математики
Воронеж
2023 год
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 4
1. Основная часть 4
1.1 Определение «Софизм» 4
1.2 История софизмов 5
1.3 Классификация софизмов 7
1.4. Применение математических софизмов 8
2 Исследовательская часть 8
2.1 Практические задачи 8
2.2 Классификация ошибок 10
ЗАКЛЮЧЕНИЕ 12
СПИСОК ЛИТЕРАТУРЫ 14
Паспорт проекта
| | Название проекта | Математические софизмы |
| | ФИО разработчика проекта | Сапрыкин Давид Русланович |
| | ФИО руководителя проекта или консультанта, должность | Попова Марина Алексеевна, преподаватель математики |
| | Название образовательного учреждения | Государственное бюджетное профессиональное образовательное учреждение Воронежской области «Воронежский индустриальный колледж» |
| | Год разработки проекта | 2023 год |
| | Актуальность | Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. |
| | Объект исследования | Софизмы, их виды |
| | Предмет исследования | Математические софизмы |
| | Гипотеза | Софизм – это обман |
| | Цель | Узнать, что такое математические софизмы |
| | Задачи | 1. Познакомиться с понятием – софизм. 2. Узнать виды математических софизмов. 3. Рассмотреть примеры математических софизмов. 4. Понять где используются математические софизмы. |
| | Тип проекта | Исследовательский |
| | Сфера применения результатов | На уроках математики |
| | Форма продукта проектной деятельности | Информационный; по предметно - содержательной линии: межпредметный. |
| | Предметная область | Математика |
ВВЕДЕНИЕ
Наверняка, каждый человек хоть раз в жизни слышал подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем». На самом деле, таких примеров можно привести очень много, но что все они обозначают? Кто их выдумал? Имеют ли они какое-нибудь логическое объяснение или же это лишь вымысел???
Именно эти вопросы я хочу рассмотреть в своей работе, название которой – «Математические софизмы». Неслучайно я выбрал именно математические софизмы (хотя бывают и логические, и словесные). Они, как мне кажется, более интересны, имеют четкое логическое объяснение, кроме того, с математическими софизмами мы встречаемся намного чаще, чем с обычными. Само понятие математических софизмов предполагает несколько видов софизмов, ведь в математические можно включить и алгебраические, и геометрические, и простейшие арифметические.
1. Основная часть
1.1 Определение «Софизм»
Софизм – (от греческого sophisma , «мастерство, умение, хитрая выдумка, уловка») - умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям.
Софизм, в отличие от паралогизма, основан на преднамеренном, сознательном нарушении правил логики. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок.
Итак, софизм — всего лишь сбивчивое доказательство, попытка выдать ложь за истину. Он имеет случайный, не связанный с существом рассматриваемой темы характер и является сугубо внешним препятствием на пути проводимого рассуждения. Отсюда следует, что никакого глубокого и требующего специального разъяснения содержания за ним не стоит. В софизме как результате заведомо некорректного применения семантических и логических операций не проявляются также какие-либо действительные логические трудности. Коротко говоря, софизм — это мнимая проблема.
В обычном и распространенном понимании софизм — это умышленный обман, основанный на нарушении правил языка или логики. Но обман тонкий и завуалированный, так что его не сразу и не каждому удается раскрыть. Цель его — выдать ложь за истину. Прибегать к софизмам предосудительно, как и вообще обманывать и внушать ложную мысль.
Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записи чертежей, за законностью математических операций. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.
1.2 История софизмов
Софистами называли группу древнегреческих философов 4-5 века до н.э., достигших большого искусства в логике. В период падения нравов древнегреческого общества (5 век) появляются так называемые учителя красноречия, которые целью своей деятельности считали и называли приобретение и распространения мудрости, вследствие чего они именовали себя софистами. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса. Но суть деятельности софистов много больше, чем простое обучение искусству красноречия. Они обучали и просвещали древнегреческий народ, старались способствовать достижению нравственности, присутствия духа, способности ума ориентироваться во всяком деле. Но софисты не были учеными. Умение, которое должно было быть достигнуто с их помощью, заключалось в том, что человек учился иметь в виду многообразные точки зрения. Аристотель называл софизмом «мнимые доказательства», в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению, вызванному недостаточностью логического анализа.
Убедительность на первый взгляд многих софизмов, их «логичность» обычно связана с хорошо замаскированной ошибкой — семиотической: за счёт метафоричности речи, нарушающих однозначность мысли и приводящих к смешению значений терминов, или же логической: подмена основной мысли (тезиса) доказательства, принятие ложных посылок за истинные, несоблюдение допустимых способов рассуждения (правил логического вывода), использование «неразрешённых» или даже «запрещённых» правил или действий, например деления на нуль в математических софизмах. Исторически с понятием «софизм» неизменно связывают идею о намеренной фальсификации, руководствуясь признанием Протагора, что задача софиста (софист, от греч. sophistes — умелец, изобретатель, мудрец, лжемудрец) — представить наихудший аргумент как наилучший путём хитроумных уловок в речи, в рассуждении, заботясь не об истине, а об успехе в споре или о практической выгоде. Однако софизмы существовали задолго до философов-софистов, а наиболее известные и интересные были сформулированы позднее в сложившихся под влиянием Сократа философских школах. Термин “софизм” впервые ввел Аристотель, охарактеризовавший софистику как мнимую, а не действительную мудрость. К софизмам им были отнесены и апории Зенона, направленные против движения и множественности вещей, и рассуждения собственно софистов, и все те софизмы, которые открывались в других философских школах. Это говорит о том, что софизмы не были изобретением одних софистов, а являлись скорее чем-то обычным для многих школ античной философии.
1.3 Классификация софизмов
Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашел ошибку в софизме, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать. Виды математических софизмов: арифметические софизмы, алгебраические софизмы, геометрические софизмы. Математические софизмы развивают наблюдательность и вдумчивость, приучают тщательно следить за точностью математических рассуждений.
Алгебраические софизмы:
Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Задачи, а также методы, отличающие её от других отраслей математики, создавались постепенно, начиная с древности. Алгебра возникла под влиянием нужд общественной практики, в результате поисков общих приёмов для решения однотипных арифметических задач. Приёмы эти заключаются обычно в составлении и решении уравнений. Т.е. алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.
Геометрические софизмы:
Умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.
Арифметические софизмы:
Это числовые выражения имеющие неточность или ошибку, незаметную с первого взгляда.
Логические софизмы:
Это софизмы, ошибки которых заключаются в неправильных рассуждениях.
1.4. Применение математических софизмов
1. На уроках, чтобы сделать их более интересными, для создания проблемных ситуаций;
2. В домашних задачах, для более осмысленного понимания материала, пройденного на уроках (найти ошибку в МС, придумать свои МС);
3. При проведении различных математических соревнований, для разнообразия;
4. На занятиях факультативов, для более глубокого изучения тем математики;
5. При написании реферативных и исследовательских работ.
2 Исследовательская часть
2.1 Практические задачи
1. Пример алгебраического софизма:
«Два неодинаковых натуральных числа равны между собой» решим систему двух уравнений:
х+2у=6, (1)
у=4- х/2 (2)
Сделаем это подстановкой у из 2го уравнения в 1, получаем х+8-х=6, откуда 8=6
Где же ошибка???
Уравнение (2) можно записать как х+2у=8, так что исходная система запишется в виде:
Х+2у=6,
Х+2у=8
В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения. Графически это означает, что прямые у=3-х/2 и у=4-х/2 параллельны и не совпадают. Перед тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно много решений или не имеет решений вообще.
2. Пример арифметического софизма:
«Пять равно шести».
Возьмем тождество 35+10-45=42+12-54.
В каждой части вынесем за скобки общий множитель: 5(7+2-9)=6(7+2-9) , так как вторые множители равны, то и первые множители тоже равны, получим 5=6.
Где ошибка???
Ошибка допущена при делении верного равенства 5(7+2- 9) = 6(7+2-9) на число 7+2-9, равное 0. Этого нельзя делать. Любое равенство можно делить только на число, отличное от 0.
3. Пример геометрического софизма:
«Катет равен гипотенузе»
Угол С равен 90˚, ВД - биссектриса угла СВА, СК = КА, ОК перпендикулярна СА, О - точка пересечения прямых ОК и ВД, ОМ перпендикулярна АВ, ОL перпендикулярна ВС. Имеем: треугольник LВО равен треугольнику МВО, ВL = ВМ, ОМ = ОL = СК = КА, треугольник КОА равен треугольнику ОМА (ОА - общая сторона, КА = ОМ, угол ОКА и угол ОМА - прямые), угол ОАК = углу МОА, ОК = МА = СL, ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому ВА = ВС.
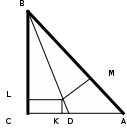
O
Где ошибка???
Ошибка заключается в том, что рассуждения, о том, что катет равен гипотенузе, опирались на ошибочный чертеж. Точка пересечения прямой, определяемой биссектрисой ВD и серединного перпендикуляра к катету АС, находится вне треугольника АВС.
4. Пример логического софизма:
«Четное и нечетно»
5 есть 2+3 («два и три»). Два - число четное, три – нечетное, выходит, что число пять – число и четное и нечетное.
Где ошибка???
Пять не делится на два, также, как и 2+3, значит, оба числа нечетные.
2.2 Классификация ошибок
1. Терминологические ошибки.
Грамматические, терминологические и риторические источники софизмов выражаются в неточном или неправильном словоупотреблении и построении фразы наиболее характерные: