Файл: Лабораторная работа 12 Тестирование по принципу черного ящика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 229
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- для определения типа и существования первой прямой;
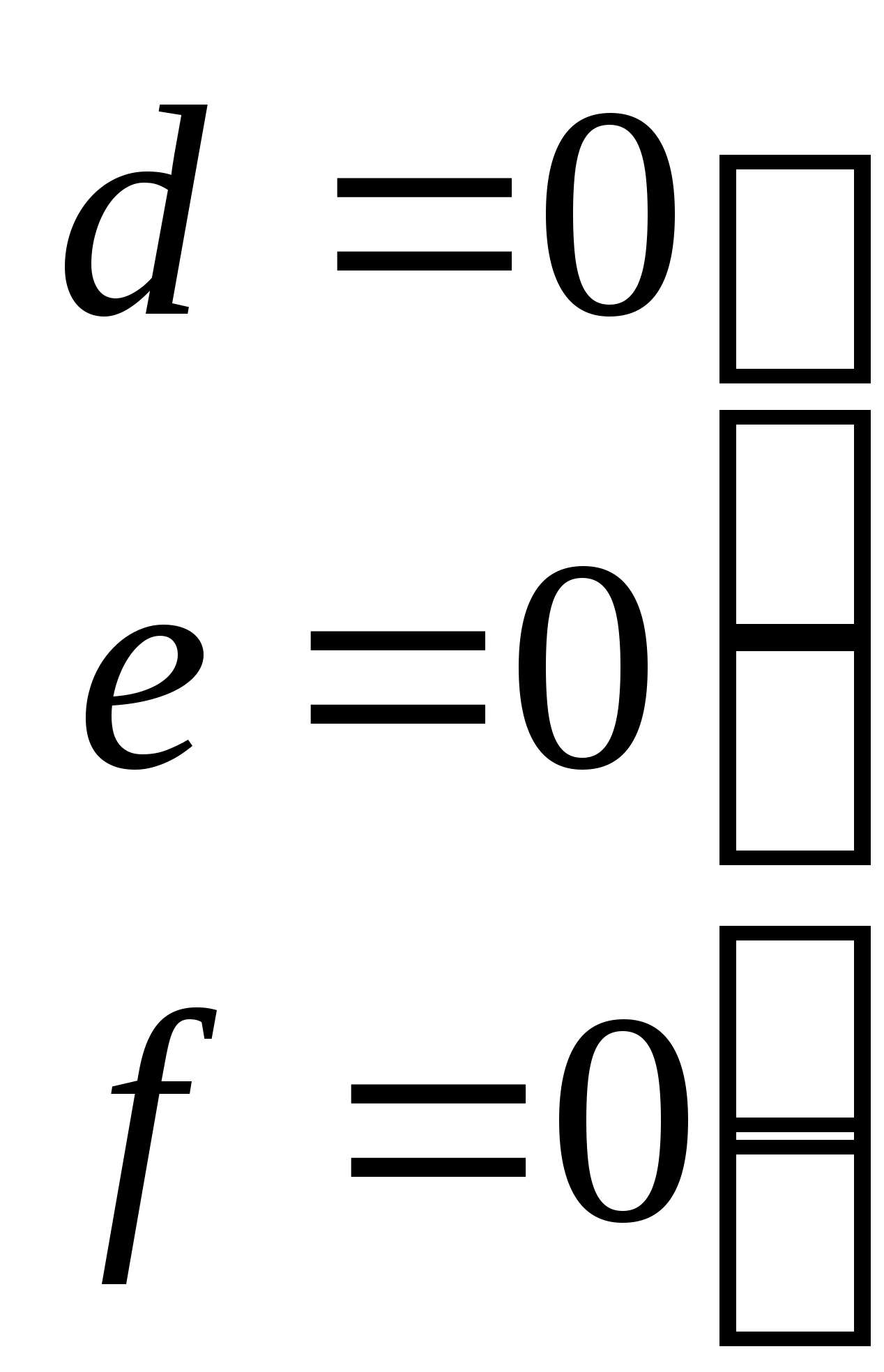- для определения типа и существования второй прямой;
б) для определения точки пересечения:
= 0
x = 0
y = 0
Выделяем три группы причинно-следственных связей (определение типа и существования первой линии, определение типа и существования второй линии, определение точки пересечения) и строим таблицы истинности.
Такая же таблица строится для второй прямой.
Каждая строка этих таблиц преобразуется в тест. При возможности (с учетом независимости групп) берутся данные, соответствующие строкам сразу двух или всех трех таблиц.
В результате к уже имеющимся тестам добавляются:
2.4. По методу предположения об ошибке добавим тест:
все коэффициенты - нули.
Всего получили 20 тестов по всем четырем методикам. Если еще попробовать вложить независимые проверки, то возможно число тестов можно еще сократить. (Не забудьте для каждого теста заранее указывать результат!).
3.Общая стратегия тестирования.
Все методологии проектирования тестов могут быть объединены в общую стратегию. Это оправдано тем, что каждый метод обеспечивает создание определенного набора тестов, но ни один из них сам по себе не может дать полный набор тестов. Приемлемая стратегия состоит в следующем:
Варианты заданий:
Задача 1.
Разработать программу решения уравнения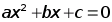
, где a, b, c - любые вещественные числа.
Задача 2.
Разработать программу определения суммарной длины тени, которую отбрасывают на ось ОХ отрезки, параллельные этой оси и заданные координатами x начала и конца отрезка:
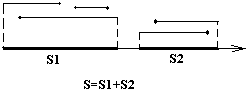
Задача 3.
Разработать программу исследования уравнений второго порядка с двумя неизвестными Ax2+2Bxy+Cy2+2Dx+2Ey+F=0. Программа должна определять вид графика: эллипс, парабола, гипербола, две пересекающиеся прямые, две параллельные прямые, две мнимые прямые.
Примечание. Вид прямой второго порядка определяется по двум дискриминантам
большому: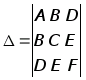
и малому 
.
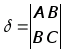Малый дискиминант для эллипса положителен, для гиперболы отрицателен, для параболы равен нулю. Если большой дискриминант равен нулю, то линия второго порядка распадается на две прямых:
для эллиптического вида - пересекающиеся мнимые прямые (точка), для гиперболического вида - пара пересекающихся действительных прямых, для параболического вида - две параллельные прямые.
Задача 4.
Разработать программу определения вида треугольника, заданного длинами его сторон: равносторонний, равнобедренный, прямоугольный, разносторонний.
Задача 5.
Разработать программу определения вида четырехугольника, заданного координатами вершин на плоскости: квадрат, прямоугольник, параллелограмм, ромб, равнобедренная трапеция, прямоугольная трапеция, трапеция общего вида, четырехугольник общего вида.
Задача 6.
Разработать программу, определяющую взаимное расположение прямых в пространстве: параллельны, пересекаются, скрещиваются и отдельно, расположение каждой прямой (параллельна оси, перпендикулярна плоскости или общего расположения). Прямые задаются координатами двух точек.
Примечание. Две прямые лежат в одной плоскости, если
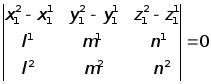
, прямые параллельны если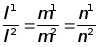
,
где l=x2-x1, m=y2-y1, n=z2-z1 (верхний индекс соответствует номеру прямой).1>
- для определения типа и существования второй прямой;б) для определения точки пересечения:
= 0
x = 0
y = 0
Выделяем три группы причинно-следственных связей (определение типа и существования первой линии, определение типа и существования второй линии, определение точки пересечения) и строим таблицы истинности.
| A=0 | B=0 | C=0 | Результат |
| 0 | 0 | X | прямая общего положения |
| 0 | 1 | 0 | прямая, параллельная оси ОХ |
| 0 | 1 | 1 | ось ОХ |
| 1 | 0 | 0 | прямая, параллельная оси ОУ |
| 1 | 0 | 1 | ось ОУ |
| 1 | 1 | Х | множество точек плоскости |
Такая же таблица строится для второй прямой.
| = 0 | x = 0 | y = 0 | Ед. реш. | Мн.реш. | Реш. нет |
| 0 | X | X | 1 | 0 | 0 |
| 1 | 0 | X | 0 | 0 | 1 |
| 1 | X | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 |
Каждая строка этих таблиц преобразуется в тест. При возможности (с учетом независимости групп) берутся данные, соответствующие строкам сразу двух или всех трех таблиц.
В результате к уже имеющимся тестам добавляются:
-
проверки всех случаев расположения обеих прямых - 6 тестов по первой прямой вкладываются в 6 тестов по второй прямой так, чтобы варианты не совпадали, - 6 тестов; -
выполняется отдельная проверка несовпадения условия x = 0 или y = 0 (в зависимости от того, какой тест был выбран по методу граничных условий) - тест также можно совместить с предыдущими 6 тестами;
2.4. По методу предположения об ошибке добавим тест:
все коэффициенты - нули.
Всего получили 20 тестов по всем четырем методикам. Если еще попробовать вложить независимые проверки, то возможно число тестов можно еще сократить. (Не забудьте для каждого теста заранее указывать результат!).
3.Общая стратегия тестирования.
Все методологии проектирования тестов могут быть объединены в общую стратегию. Это оправдано тем, что каждый метод обеспечивает создание определенного набора тестов, но ни один из них сам по себе не может дать полный набор тестов. Приемлемая стратегия состоит в следующем:
-
Если спецификация состоит из комбинации входных условий, то начать рекомендуется с применения метода функциональных диаграмм. -
В любом случае необходимо использовать анализ граничных значений. -
Определить правильные и неправильные классы эквивалентности для входных и выходных данных и дополнить, если это необходимо, тесты, построенные на предыдущих шагах. -
Для получениядополнительных тестов рекомендуется использовать метод предположения об ошибке.
-
Ознакомиться с теоретическими сведениями по стратегиям тестирования. -
В соответствии с вариантом задачи, подготовить тесты по методикам стратегии "черного ящика". -
Предлагаемые тесты свести в таблицу.
Номер теста
Назначение теста
Значения исходных данных
Ожидаемый результат
Реакция программы
Вывод
-
Разработать программу. -
Выполнить тестирование. Занести в таблицу результаты. -
Сделать вывод о роли тестирования с использованием стратегии "черного ящика" и возможностях его применения. Сформулировать его достоинства и недостатки.
Варианты заданий:
Задача 1.
Разработать программу решения уравнения
, где a, b, c - любые вещественные числа.Задача 2.
Разработать программу определения суммарной длины тени, которую отбрасывают на ось ОХ отрезки, параллельные этой оси и заданные координатами x начала и конца отрезка:
Задача 3.
Разработать программу исследования уравнений второго порядка с двумя неизвестными Ax2+2Bxy+Cy2+2Dx+2Ey+F=0. Программа должна определять вид графика: эллипс, парабола, гипербола, две пересекающиеся прямые, две параллельные прямые, две мнимые прямые.
Примечание. Вид прямой второго порядка определяется по двум дискриминантам
большому:
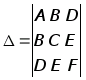и малому .Малый дискиминант для эллипса положителен, для гиперболы отрицателен, для параболы равен нулю. Если большой дискриминант равен нулю, то линия второго порядка распадается на две прямых:
для эллиптического вида - пересекающиеся мнимые прямые (точка), для гиперболического вида - пара пересекающихся действительных прямых, для параболического вида - две параллельные прямые.
Задача 4.
Разработать программу определения вида треугольника, заданного длинами его сторон: равносторонний, равнобедренный, прямоугольный, разносторонний.
Задача 5.
Разработать программу определения вида четырехугольника, заданного координатами вершин на плоскости: квадрат, прямоугольник, параллелограмм, ромб, равнобедренная трапеция, прямоугольная трапеция, трапеция общего вида, четырехугольник общего вида.
Задача 6.
Разработать программу, определяющую взаимное расположение прямых в пространстве: параллельны, пересекаются, скрещиваются и отдельно, расположение каждой прямой (параллельна оси, перпендикулярна плоскости или общего расположения). Прямые задаются координатами двух точек.
Примечание. Две прямые лежат в одной плоскости, если
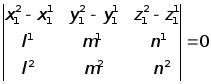
, прямые параллельны если
,где l=x2-x1, m=y2-y1, n=z2-z1 (верхний индекс соответствует номеру прямой).1>