ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 86
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант № 9.
Найдите решение матричной игры: p1, p2, q1, q2, v
Таблица 1.
| | B1 | B2 |
| А1 | 5 | 2 |
| А2 | 4 | 1 |
| А3 | 1 | 1 |
| А4 | 6 | 4 |
| А5 | 1 | 9 |
Решение:
1. Проверим, имеет ли платежная матрица седловую точку.
Определим оптимальные стратегии игроков. Начнем со стратегии первого игрока, который стремится максимизировать свой выигрыш, учитывая то, что второй игрок будет пытаться свести выигрыш первого игрока к минимуму.
Запишем минимальные выигрыши в правый столбец:
Таблица 2.
| | B1 | B2 | |
| А1 | 5 | 2 | 2 |
| А2 | 4 | 1 | 1 |
| А3 | 1 | 1 | 1 |
| А4 | 6 | 4 | 4 |
| А5 | 1 | 9 | 1 |
Первый игрок выбирает стратегию А4, при которой его минимальный выигрыш максимален:
max min = 4
Таким образом, если первый игрок выберет стратегию А4, ему гарантирован выигрыш не меньший, чем 4, при любом поведении второго игрока.
Рассмотрим теперь поведение второго игрока. Запишем максимальные выигрыши в нижней строке.
Таблица 3.
| | B1 | B2 | |
| А1 | 5 | 2 | 2 |
| А2 | 4 | 1 | 1 |
| А3 | 1 | 1 | 1 |
| А4 | 6 | 4 | 4 |
| А5 | 1 | 9 | 1 |
| | 6 | 9 | |
Второй игрок выбирает стратегию B1, при которой максимальный выигрыш первого игрока минимален:
min max = 6.
То есть, если второй игрок будет придерживаться стратегии B1, то при любом поведении первого игрока он не проиграет больше, чем 6.
В данной задаче max min и min max не совпали, что свидетельствует об отсутствии седловой точки. Тогда цена игры находится в пределах
4≤v≤6.
Находим решение игры в смешанных стратегиях.
2. Проверим платежную матрицу на доминирующие строки и доминирующие столбцы.
Стратегия A1 доминирует над стратегией A2 (все элементы строки 1 больше или равны значениям 2-ой строки), следовательно, исключаем 2-ую строку матрицы. Вероятность p2= 0.
Стратегия A1 доминирует над стратегией A3 (все элементы строки 1 больше или равны значениям 3-ой строки), следовательно, исключаем 3-ую строку матрицы. Вероятность p3= 0.
Стратегия A4 доминирует над стратегией A1 (все элементы строки 4 больше или равны значениям 1-ой строки), следовательно, исключаем 1-ую строку матрицы. Вероятность p1= 0.
| 6 | 4 |
| 1 | 9 |
Таким образом, свели игру 5 x 2 к игре 2 x 2.
Так как игроки выбирают свои чистые стратегии случайным образом
, то выигрыш игрока А будет случайной величиной. В этом случае игрок А должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.
Аналогично, игрок В должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока А.
3. Находим решение игры в смешанных стратегиях.
Запишем систему уравнений.
Для игрока А:
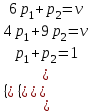
Для игрока В:
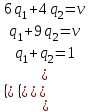
Решая эти системы методом Гаусса, находим
v = 5
p1 = 4/5 (вероятность применения 1-ой стратегии).
p2 = 1/5 (вероятность применения 2-ой стратегии).
Оптимальная смешанная стратегия игрока А: P = (4/5; 1/5)
q1 = 1/2 (вероятность применения 1-ой стратегии).
q2 = 1/2 (вероятность применения 2-ой стратегии).
Оптимальная смешанная стратегия игрока В: Q = (1/2; 1/2)
Цена игры:
v = 5
Ответ: p1 = 4/5, p2 = 1/5, q1 = 1/2, q2 = 1/2, v = 5