Файл: Реферат по дисциплине Структуры и алгоритмы обработки данных.rtf
Добавлен: 22.11.2023
Просмотров: 135
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Отыскание функций сложности алгоритмов важно как с прикладной, так и с теоретической точек зрения. В практике проектирования систем реального времени задача разработки программы формулируется так: отыскать такой алгоритм a, решающий задачу P, что Тa(X) < Tmax при X Î D, где D - область допустимых значений входных данных (задача с ограничением на временную сложность). В системах, где критерий качества связан с временем ожидания реакции компьютера (системы управления базами данных, системы автоматического перевода для естественных языков программы для игры в шахматы и другие) задача может быть поставлена так: отыскать среди всех алгоритмов, решающих задачу Р, такой алгоритм а, для которого функция Ta(X) будет принимать минимальные значения на выбранном подмножестве S значений исходных данных, XÎSÌD (задача минимизации временной сложности; дополнительно формулируются ограничения по емкостной сложности).
Двойственная задача минимизации емкостной сложности при ограничениях на временную сложность возникает реже в силу архитектурных особенностей современных ЭВМ, поскольку запоминающие устройства разных уровней, входящие в состав машины, построены так, что программе может быть доступна очень большая, практически неограниченная область памяти - виртуальная память. Недостаточное количество основной памяти приводит лишь к некоторому замедлению работы из-за обменов с диском. Так как в любой момент времени программа работает лишь с двумя-тремя значениями и использование кэша и аппаратного просмотра команд программы вперед позволяет заблаговременно перенести с диска в основную память нужные значения, то можно констатировать, что минимизация емкостной сложности не является первоочередной задачей.
3. Верхние и средние оценки сложности алгоритмов
Многие задачи характеризуются большим количеством исходных данных. Вводя интегральный параметр V объема (сложности) данных, неявно предположено, что все множество комбинаций значений исходных данных может быть разбито на классы. В один класс попадают комбинации с одним и тем же значением V. Для любой комбинации из заданного класса алгоритм будет иметь одинаковую сложность (исполнитель выполнит одно и то же количество операций). Иначе говоря, функция c = сложность_a(X) может быть разложена в композицию функций V= r(Х) и c = Тa(V), где r - преобразование значений x1, x2, x3, ...,xn в значение V (8, стр. 117-119).
Но нет никаких причин надеяться, что это будет выполняться для любых алгоритмов, учитывая наше желание представлять функции формулами с использованием общеизвестных элементарных функций (или, как говорят, в аналитическом виде). Выход состоит в следующем. Множество D комбинаций исходных данных все-таки разбивается "каким-либо разумным образом" на классы, и каждому классу приписывается некоторое значение переменной V. Например, если мы хотим оценить сложность алгоритма анализа арифметических выражений, то в один класс можно поместить все выражения, состоящие из одинакового числа символов (строки одинаковой длины) и переменную V сделать равной длине строки. Это разумное предположение, так как с увеличением длины сложность должна увеличиваться: припишем к выражению длины n строку +1 - получится выражение длины n+2, требующее для анализа больше операций, чем предыдущее. Но строгого (линейного) порядка нет. Среди выражений длины n может найтись более сложное (в смысле анализа), чем некоторое выражение длины n+2, не говоря уже о том, что среди выражений равной длины будут выражения разной сложности.
Затем для каждого класса (с данным значением V) оценивается количество необходимых операций в худшем случае, т.е. для набора исходных данных, требующих максимального количества операций обработки (сложность для худшего случая - верхняя оценка), и в лучшем случае - для набора, требующего минимального количества операций. Таким образом, получаются верхняя и нижняя оценки сложности алгоритма (рисунок 1).
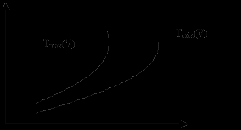
Рис.1. Зависимость сложности алгоритма от сложности данных
Разница между Tmax(V) и Tmin(V) может быть значительной. Но для многих алгоритмов отмечается ситуация "редкости крайних значений": только на относительно небольшом количестве сочетаний исходных данных реализуются близкие к верхним или нижним оценкам значения сложности. Поэтому интересно бывает отыскать некоторое "усредненное" по всем данным число операций (средняя оценка). Для этого привлекаются комбинаторные методы или методы теории вероятностей. Полученное значение и считается значением Тa(V) средней оценки.
Системы реального времени, работающие в очень критических условиях, требуют, чтобы неравенство Тa(X)
4. Основные методы и приемы анализа сложности
Отыскание функции сложности производится на основе анализа текста алгоритма. Для определенности будем считать, что алгоритм записан на универсальном языке программирования типа Паскаля и содержит явно записанные арифметические операции, операции сравнения и пересылки скалярных данных, управляющие конструкции циклов и выбора. Если встречаются вызовы процедур, то вызов не рассматривается как одна операция: вызов вносит вклад в общую сумму на основе подсчета количества операций в вызываемой процедуре, плюс собственно оператор вызова (с единичной сложностью) (3, стр. 108-119). С целью анализа алгоритм (программу) удобно представлять управляющим графом (родственное понятие - схема алгоритма). Управляющий граф строится следующим образом. Каждому оператору присваивания или вызову процедуры ставится в соответствие вершина графа (точка). Два последовательно записанных оператора (последовательно исполняемых) изображаются вершинами, соединенными стрелкой, указывающей порядок исполнения (рис. 2) (3, стр. 122).
Рис.2. Граф линейного участка
Последовательность из нескольких операторов присваивания или вызовов процедур изображается цепью и называется линейным участком.
Условный оператор изображается вершиной, соответствующей вычислению условия, и двумя выходящими дугами с приписанными им вариантами then, else (рис. 3).
if a < b then x := аx := b;
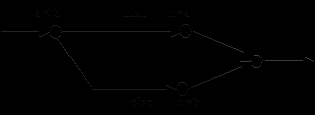
Рис.3. Граф условного оператора
Если после then записан составной оператор (линейный участок), то в управляющем графе ему соответствует цепь. Условный оператор задает разветвление в управляющем графе, заканчивающееся пустой вершиной (без операций), помеченной точкой с запятой. Если в операторе часть else отсутствует, то нижняя ветка включает пустую вершину. Подобный фрагмент в управляющем графе порождает оператор выбора case, но только разветвление может быть на большее число ветвей и выходящие дуги помечаются соответствующими константами (рис.4).
Рис.4. Граф оператора разветвления
Операторы цикла (рисунок 5) изображаются в управляющем графе замкнутой последовательностью вершин (циклом).
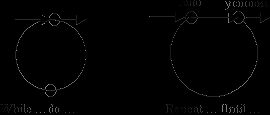
Рис.5. Графы операторов цикла
Кроме этого в управляющем графе вводится одна начальная вершина и одна или несколько заключительных вершин. Каждой вершине графа припишем число - количество операций, которые необходимо выполнить для выполнения оператора программы, связанного с этой вершиной. Это число назовем весом вершины. Вес пустой, начальной и заключительных вершин равен нулю. Если из вершины выходит две или более дуги, то каждой из них припишем условие, при выполнении которого вычислительный процесс пойдет в этом направлении. Эти условия будем называть пометками дуг. Таким образом, управляющий граф программы представляет собой направленный взвешенный граф.
Необходимо рассмотреть следующие несколько случаев (6, стр. 172-178):
Управляющий граф представляет собой линейный участок. Сложность равна сумме весов вершин, принадлежащих линейному участку, и является константой, если на участке нет вершин - вызовов процедур. Если такие вершины есть, то их вес равен функциям сложности соответствующих процедур.
Управляющий граф содержит разветвления, но не содержит циклов. Это означает, что вычислительный процесс в зависимости от исходных данных может направиться по одной из конечного числа ветвей, начинающихся в начальной вершине и заканчивающихся в одной из конечных вершин. Расчет функции сложности зависит от того, рассматривается худший случай или средний случай.
Управляющий граф содержит цикл, порожденный оператором for. Если выражения, определяющие начальное и конечное значения параметра цикла суть константы, то нетрудно подсчитать, сколько раз будет выполняться тело цикла и умножить на этот коэффициент вес тела цикла. Если выражения зависят от исходных данных, то можно оценить значение разности этих выражений в худшем или среднем случаях.
Управляющий граф содержит цикл, порожденный операторами while или repeat. Циклы while и repeat могут вызвать больше затруднений при анализе, чем оператор for, так как количество исполнений тела цикла зависит от истинности или ложности условия, а переменные, входящие в состав условия изменяются в теле цикла, причем оценить величину и направленность этого изменения достаточно сложно.
Управляющий граф содержит разветвлении. Для худшего случая нужно вычислить вес каждой ветви как сумму весов входящих в нее вершин, после чего найти максимальный из весов ветвей. Это и будет сложностью процедуры.
Пример 1. Управляющий граф содержит 10 вершин с весом {3, 5, 1,4, 3, 4, 6, 8, 5, 3}. Вершина 3 (вес равен 1) соответствует вычислению условия в операторе if; вершины 4, 5, 6 входят в часть then, вершины 7, 8 входят в часть else. Таким образом, имеется две ветви с весом 3+5+1+4+3+4+5+3 = 28 и 3+5+1+6+8+5+3 = 31; сложность равна 31.
Пример 2. Тот же граф, что и в примере 1, но вершина 8 соответствует вызову процедуры, имеющей сложность 2V + 1. В этом случае функция сложности равна max (28, 2V+24 ) = 24+max(4, 2V) = 24 + 2 max ( 2, V ).
Для среднего случая, кроме веса ветвей, нужно оценить еще и частоты ветвей. Под частотой ветви понимается отношение числа выполнений программы, при которых исполнялись операторы, принадлежащие данной ветви, к общему числу выполнений программы. Тогда сложность программы будет вычисляться как сумма произведений весов ветвей на их частоты. Если все комбинации исходных данных программы равновероятны, то частоты ветвей можно оценить следующим образом: (7, стр. 188)
Пусть управляющий граф содержит разветвления с условиями C1, C2, C3, ..., Cn, причем проверка условия C1 производится всегда первой по ходу выполнения программы. Следовательно, условие С1 разбивает все ветви на две группы: для ветвей первой группы это условие истинно, а для ветвей второй группы - ложно. Условие С2 разбивает группу ветвей с истинным условием С1 на две группы, удовлетворяющие условиям C1 and C2 и C1 and not С2. Условие С3 порождает группы ветвей, удовлетворяющих условиям not C1 and С3 и not C1 and not С3 и т. д. Множество D комбинаций исходных данных также делится на две части D1 и D2 и это деление порождается условием C1 даже, если сами исходные данные не входят в формулировку условия, а входят только константы и промежуточные переменные. В свою очередь, D1 делится на подмножества D2 и D3 в соответствии с условием C2 и так далее. На рисунке 1 изображены примеры управляющего графа программы и разбиений областей D. Три условных оператора изображены черными вершинами, область D делится сначала сплошной линией на подобласти D1 и D2, а затем каждая из них делится пунктирными линиями на подобласти D3, D4 и D5, D6.
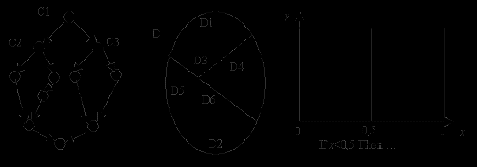
Рис.6. Управляющий граф и разбиение области данных
Каждая подобласть, не разделенная на более мелкие части, соответствует одной ветви в управляющем графе. Обозначим все такие области di. Тогда, считая все комбинации исходных данных равновероятными, можем оценить частоту исполнения i-й ветви как отношение мощности множества di к мощности множества D, pi = |di|/|D|. Если i-я ветвь имеет вес li то сложность программы можно оценить величиной
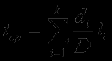, где k - количество ветвей.Пример 3. Тот же граф, что и в примере 1. Условие в операторе if имеет вид (x<0,5), где x - входная переменная, значения которой принадлежат интервалу [0,1]. Если более подробной информации о входной переменной нет, то можно предполагать, что вероятность получить на входе значение xÎ [0, 0,5] равна вероятности получить x Î [0,5, 1] и, значит та и другая вероятности равны 0,5. Следовательно, и вероятности ветвей одинаковы; средняя сложность равна 28(1/2) + 31(1/2) = 29,5 .
Пример 4 (объединение условий примеров 2 и 3). Средняя сложность равна 28(1/2) + (2V + 24)(1/2) = V + 26.
Управляющий граф содержит цикл, порожденный оператором for. Если выражения, определяющие начальное и конечное значения параметра цикла - константы, то подсчитываем, сколько раз будет выполняться тело цикла и умножаем на этот коэффициент вес тела цикла. Если выражения зависят от исходных данных, то оцениваем значение разности этих выражений в худшем или среднем случаях.
Пример 5. Процедура содержит цикл
for i := 1 to x do
<тело цикла>,
где x - входная переменная, xÎ[1,100]. Тело цикла выполняется x раз, худший случай реализуется при x=100. Если предположить равновероятность различных значений x, то среднее количество выполнений тела цикла равно (1/100)(1+2+3+ ...+100)=50,5.
Пример 6. Процедура содержит вложенные циклы:
for i := 1 to x doj := i to x do
<тело цикла>;
входная переменная xÎ[1, 5]. Тело цикла выполняется x + (x-1)+(х-2)+ ...+ 1 = x (х+1)/2 раз. Верхняя граница сложности = max = (x (х+1)/2) = 13. Среднее значение сложности подсчитать несколько труднее. Снова положим, что все 5 возможных значений x равновероятны. Тогда среднее значение сложности равно:
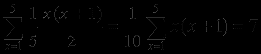
Управляющий граф содержит цикл, порожденный операторами while или repeat. Циклы while и repeat анализировать сложнее, чем оператор for, так как количество исполнений тела цикла зависит от истинности или ложности условия и, может быть, достаточно сложных изменений в теле цикла значений переменных, входящих в состав условия.