Файл: Реферат по дисциплине Структуры и алгоритмы обработки данных.rtf
Добавлен: 22.11.2023
Просмотров: 136
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рассмотрим в качестве примера (4, стр. 334) вычисление
методом Ньютона (имеется в виду вычисление вещественного значения корня). Задача сводится к нахождению корня уравнения x(1/p) - z = 0, который, в свою очередь, отыскивается с помощью итерационного процесса
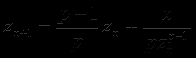
начинающегося некоторым начальным значением z0, выбираемым возможно наиболее близким к корню. Окончание процесса происходит, когда корень оказывается найденным с заданной точностью e с помощью, например, следующей функции.
function P_root( p: integer; x, z0, epsilon: real ): real;: integer;, z: real;:= z0;:= z;
у := old;i:= 2 to p - 1 do у:= y*old;:= (p - l)*old/p + x/ (p*y);abs( z - old ) < epsilon;
end;
Из теории численных методов известно, что требуемое количество n итераций для достижения заданной точности имеет порядок
. Этот процесс сходится (заканчивается) очень быстро: уже при 5 итерациях достигается точность выше 10-9.В общем случае условие в операторе while или в операторе repeat делит область комбинаций исходных и промежуточных данных, т.е. область возможных состояний программы на момент начала исполнения оператора цикла на две части: для первой условие выполняется, а для второй - нет. Если начальное состояние принадлежит первой подобласти (для while) или второй подобласти (для repeat), то с каждым выполнением тела цикла состояние (как точка в пространстве состояний) будет перемещаться по некоторой траектории, зависящей от операций, заданных в теле, до тех пор, пока не пересечет границу области. Именно количество шагов до пересечения границы и определяет сложность этого участка программы.
5. Анализ сложности рекурсивных алгоритмов
Рассмотрим сначала случай прямой рекурсии с единственным (вне какого-либо цикла) рекурсивным вызовом в теле процедуры. Примером такого алгоритма является алгоритм Евклида вычисления наибольшего общего делителя. Текст рекурсивной процедуры с вектором исходных данных X содержит вызов этой же процедуры с измененным по некоторому правилу вектором исходных данных Y = f(X). Кроме этого, в тексте содержится некоторое нерекурсивное вычисление h(X) и операции сравнения c(Х,S) значения X со значением S, при котором рекурсивный процесс должен заканчиваться. Обозначим "точное" (а не верхнюю границу или среднее) значение сложности при входных данных X через Тa(X). Тогда
Тa(X) = Тa(Y)+Th(X)+Tc(X,S), или Тa(X) = Тa(АХ))+Tf(X)+Th(X)+ Tc(X,S).
Второе соотношение представляет собой рекуррентное уравнение для определения значений неизвестной функции Тa(X) через известные значения f(A), Tf(X), Th(X), Tc(X,S). Кроме этого, имеется начальное условие Ta(S)=Ts(S) с известной функцией сложности вычисления (нерекурсивного) значения S. Таким образом, имеется система:
Тa(Х) =Ta(f(X))+ Tf(X)+Th(X)+ Тc(X, S)a(S)=Tc(S,S)+Ts(S)
Это частный случай рекуррентного уравнения. Такие уравнения имеют развитую теорию. В некоторых случаях возможно аналитическое решение. Покажем его применение на примере рекурсивного вычисления факториала:
function FACTORIAL (х: integer): integer;x = 1 then FACTORIAL:= 1FACTORIAL:= x * FACTORIAL (x-1);;
Здесь X=x, S=1, f(X)=X-1, Tf(X)=1, Th(X) = 2, Tc(X,S)=l, Ts(S) = 1. Таким образом, система уравнений превращается в Тa(x) = Тa(х-1)+4, Тa(1) = 2. Ее решение - Тa(x) = 4х-2.
Верхняя оценка Тa(V) может быть получена подобным образом, но с использованием рекуррентных неравенств:
Тa(V) <= Тa(f(V))+Tf(V)+Th(V)+Tc(V,V0),a(V0) <= Tc(V0, Vo)+Ts(V0).
Оценка среднего значения сложности требует учета вероятностных законов и может быть значительно более трудной. Вообще говоря, нельзя использовать написанные выше рекуррентные уравнения в вероятностном случае: среднее значение функции случайной величины не равно значению функции от среднего значения случайной величины, среднее (f(X)) <> f(среднее (X)), кроме случая линейной функции f.
Теперь рассмотрим более общий случай прямой рекурсии (4, стр. 402-404) с несколькими рекурсивными вызовами в теле процедуры. Эти вызовы могут иметь разные аргументы Y1, Y2, . . . ,Yk, где Y1 =fl(X), Y2 =f2(X), ..., Yk=fk(X). Рекуррентное уравнение для функции сложности имеет вид
Тa(X) = Тa(f1(X)) + Тa(f2(X)) + ... + Тa(fk(X)) + Tf1(X) + Тf2(X) + ...+Тfk(X) + Тh (X) + Tc (X, S)
Тaa(S) = Tc (S, S) + Ts (S).
6. Оптимизация алгоритмов
Пока компьютерные науки не накопили достаточно сведений для того, чтобы задача минимизации могла быть поставлена с обычной для математики определенностью. Этому мешает несколько факторов.
Во-первых, сложно сформулировать критерий оптимизации, имеющий одновременно и бесспорное практическое значение и однозначно определенный в математическом плане. Например, можно поставить задачу минимизации числа команд машины Тьюринга - критерий, хорошо определенный математически; но совсем неясно его практическое значение, поскольку вряд ли реальная программа на реальном компьютере будет моделировать машину Тьюринга. Можно поставить задачу минимизации времени выполнения программы на реальной машине - ясный с практической точки зрения критерий. Однако невозможно будет решить задачу оптимизации математическими методами, так как время выполнения зависит (иногда значительно) от архитектуры ЭВМ, а архитектуру современных компьютеров не опишешь небольшим числом параметров. Важно также, что программа, работающая быстрее других на одном компьютере, может оказаться не самой быстрой на другом. Существуют даже специальные программы с общим названием benchmark, предназначенные для оценки архитектур.
Во-вторых, не совсем ясно, что такое сложность задачи. Ее можно было бы определить как минимальную из сложностей алгоритмов, решающих эту задачу. Но существует ли алгоритм минимальной сложности (как убедиться, что найденный алгоритм действительно минимальный или, напротив, не минимальный)? Есть ли к чему стремиться? И насколько труден поиск этого минимума? Эти вопросы связаны с нижней оценкой сложности алгоритмов (а не верхней, как в предыдущих шагах) (5, стр. 89-92).
Можно ли для рассматриваемой задачи доказать, что никакой решающий ее алгоритм не может быть проще этой нижней оценки? Возьмем известную задачу перемножения квадратных матриц. Приведен алгоритм сложности Тa(n) = 3n3 + n2. (8, стр. 199-203) Вероятно, это не лучший алгоритм, но какова оценка снизу? Результирующая матрица имеет n2 элементов. Для вычисления любого элемента нужна хотя бы одна операция однопроцессорной машины - два элемента за одну операцию найти нельзя. Для минимального алгоритма мы получаем неравенства n2 <= Ta, min(n) <= 3n3+n2 . Вряд ли n2 - хорошая нижняя оценка, но уже известно, что n3 нижней оценкой не является, так как найдены более быстрые алгоритмы (в частности, алгоритм Штрассена). (8, стр. 211)
Существует несколько самостоятельных аспектов оптимизации программ, из которых выделим два:
- оптимизация, связанная с выбором метода построения алгоритма;
- оптимизация, связанная с выбором методов представления данных в программе.
Первый вид оптимизации имеет глобальный характер и ведет к уменьшению порядка функции сложности - например, замена алгоритма с Тa(V) = O(FS) на алгоритм с Ta(V) = O(V4). Он зависит от того, как задача разбивается на подзадачи, насколько это разбиение свойственно самой задаче или является только искусственным приемом. Общим руководящим подходом здесь может быть последовательность действий, обратная анализу алгоритмов. При анализе по рекурсивному алгоритму строится уравнение, которое затем решается. При оптимизации реализуется цепочка:
Формула, задающая желаемую сложность ->
Соответствующее уравнение (одно из возможных) ->
Метод разбиения задачи на подзадачи.
Второй вид оптимизации, не меняя структуры программы в целом, ведет к экономии памяти и/или упрощению работы со структурами данных, повышению эффективности вспомогательных процедур, обеспечивающих "интерфейс" между прикладным уровнем (на котором мыслим в терминах высокоуровневых объектов - графов
, матриц, текстов и т. д.) и машинным уровнем, поддерживающим простейшие типы данных (числа, символы, указатели). Результатом этого обычно является уменьшение коэффициентов при некоторых слагаемых в функции сложности (при удачной оптимизации - при наиболее значимом слагаемом), но порядок функции сложности остается тем же. (7, стр. 204)
Оба вида оптимизации дополняют друг друга и могут применяться совместно.
Заключение
Теория алгоритмов - это наука, изучающая общие свойства и закономерности алгоритмов, разнообразные формальные модели их представления. На основе формализации понятия алгоритма возможно сравнение алгоритмов по их эффективности, проверка их эквивалентности, определение областей применимости.
Разработанные в 1930-х годах разнообразные формальные модели алгоритмов (Пост, Тьюринг, Черч), равно как и предложенные в 1950-х годах модели Колмогорова и Маркова, оказались эквивалентными в том смысле, что любой класс проблем, разрешимых в одной модели, разрешимы и в другой.
В настоящее время полученные на основе теории алгоритмов практические рекомендации получают всё большее распространение в области проектирования и разработки программных систем.
Одна из задач, которая обычно ставится при разработке алгоритмов и программ - минимизация требуемых программой ресурсов. Особенно это касается системного программного обеспечения: программ операционной системы, трансляторов, систем управления базами данных и знаний и т. д., т.е. программ, имеющих большое количество пользователей и испытывающих как товар, большую конкуренцию на рынке программных средств.
Теория сложности алгоритмов предлагает достаточные эффективные методы решения поставленной проблемы. Точное решение возможно в подавляющем большинстве практически важных ситуаций.
Однако по-прежнему открыты вопросы, связанные со сводимостью алгоритмов друг к другу и остается нерешенной известная проблема P=NP.
алгоритм сложность оптимизация
Список использованной литературы
1. Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы: Пер. с англ.: - М.: Издательский дом «Вильямс», 2001 г. -384 с., ил.
2. Вирт Н. Алгоритмы и структуры данных: Пер. с англ. - 2-ое изд., испр. - СПб.: Невский диалект, 2001 г. - 352 с., ил.
. Карпов Ю.Г. Теория автоматов - СПб.: Питер, 2002 г. - 224с., ил.
. Кнут Д. Искусство программирования. Тома 1, 2, 3. 3-е изд. Пер. с англ. : Уч. пос. - М.: Изд. дом "Вильямс", 2001 г.
. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. - М.: МЦНМО, 2001 г. - 960 с., 263 ил.
. Макконнел Дж. Анализ алгоритмов. Вводный курс. - М.: Техносфера, 2002 г. -304 с.
. Новиков Ф. А. Дискретная математика для программистов. - СПб.: Питер, 2001 г. - 304 с., ил.
. Романовский И.В. Дискретный анализ. Учебное пособие для студентов, специализирующихся по прикладной математике. - Издание 2-ое, исправленное. - СПб.; Невский диалект, 2000 г. - 240 с., ил.
. Успенский В.А. Машина Поста. - М.: Наука, 1999 г. - 96 с.