Файл: Динамика основным понятиями в механике являются пространство, время, механическое движение, перемещение Время.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 85
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
0 большой палец укажет направление силы Ампера.
Проводник с током создает вокруг себя магнитное поле, в это поле помещается второй проводник с током, а значит на него будет действовать сила Ампера. Направление силы Ампера зависит от направления линий индукции магнитного поля, которое в свою очередь зависит от направления тока в проводнике.
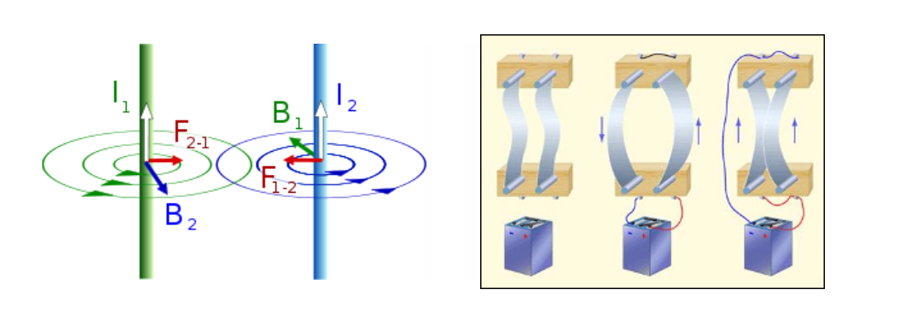
Закон Ампера – показывает, с какой силой действует магнитное поле на помещенный в него проводник:
Сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.:
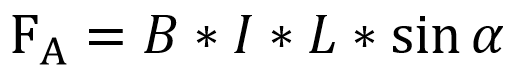
где α — угол между векторами магнитной индукции и тока,
B — индукция магнитного поля,
I — сила тока в проводнике,
L — длина проводника.
Этой формулой можно пользоваться:
если длина проводника такая, что индукция во всех точках проводника может считаться одинаковой;
если магнитное поле однородное (тогда длина проводника может быть любой, но при этом проводник целиком должен находиться в поле).
Если проводник имеет произвольную формулу и поле неоднородно, то Закон Ампера принимает вид:
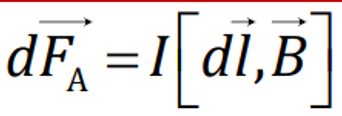
где dF — сила, с которой магнитное поле действует на бесконечно малый проводник с током I,
dl — элемент длины проводника.
К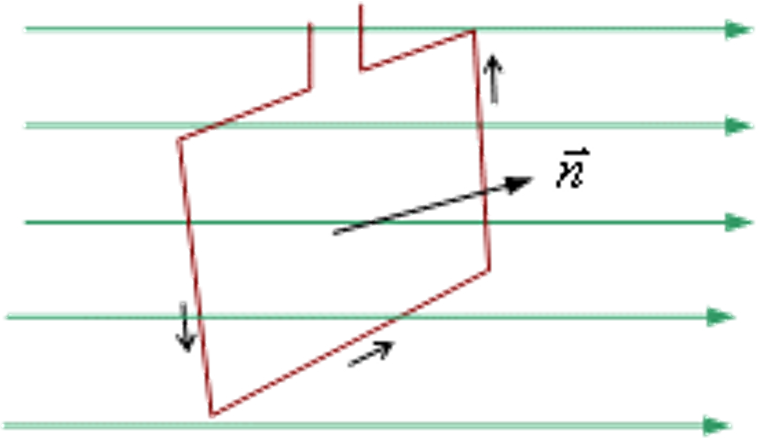 онтур с током в магнитном поле.
онтур с током в магнитном поле.
Пусть в однородное магнитное поле помещена рамка с током. Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором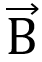 и нормалью к площади
и нормалью к площади 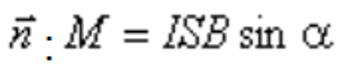 .Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке. Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:
.Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке. Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:
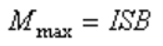 .Это выражение также можно использовать для определения индукции магнитного поля:
.Это выражение также можно использовать для определения индукции магнитного поля: 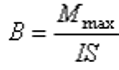 .Величину, равную произведению IS, называют магнитным моментом контура
.Величину, равную произведению IS, называют магнитным моментом контура 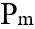 .
.
Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать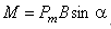 . При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.
. При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.
Магнитный момент контура с током.
Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Магнитный момент контура с током величина векторная. Он направлен по нормали к плоскости контура и связан с направлением тока правилом буравчика. Магнитный момент имеет общее значение и определяется выражением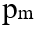 = IS для любой формы контура.
= IS для любой формы контура.

Вращательный момент – физическая величина, характеризующая вращательное действие силы на твёрдое тело.
При помещении контура с током во внешнее однородное магнитное поле на каждый элемент контура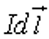 будет действовать сила Ампера. Если контур симметричный и плоский (кольцо, прямоугольник и т.д.), то силы Ампера, действующие на диаметрально противоположные участки контура, представляются "парой сил" и поворачивают контур так, что его плоскость устанавливается перпендикулярно вектору
будет действовать сила Ампера. Если контур симметричный и плоский (кольцо, прямоугольник и т.д.), то силы Ампера, действующие на диаметрально противоположные участки контура, представляются "парой сил" и поворачивают контур так, что его плоскость устанавливается перпендикулярно вектору 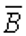 . Другими словами, на плоский симметричный контур со стороны однородного магнитного поля действует вращающий момент.
. Другими словами, на плоский симметричный контур со стороны однородного магнитного поля действует вращающий момент.
Вращательный момент контура с током можно записать
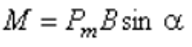 . При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.
. При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.
Действие магнитного поля на движущийся заряд.
На движущийся в магнитном поле заряд (q) со стороны магнитного поля действует сила (F), направление которой зависит от взаимного направления вектора скорости движения (v) заряда и вектора магнитной индукции поля (В). Величина силы пропорциональна скорости движения заряда и модулю магнитной индукции.
Магнитная составляющая электромагнитного поля действует на точечный заряд q, движущийся со скоростью , с силой
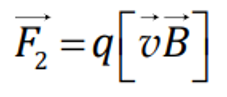
— сила Лоренца (магнитная составляющая). Направление этой силы определяют по правилу левой руки.
Сила Лоренца – сила, которая действует со стороны электромагнитного поля на движущийся электрический заряд. Весьма нередко силой Лоренца называют лишь магнитную составляющую этого поля. Формула для определения:
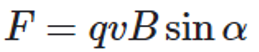
где q — заряд частицы; Е — напряжённость электрического поля; B — магнитная индукция поля; v — скорость частицы.
Она характеризуется тем, что не изменяет скорость перемещения зарядов, а лишь воздействует на вектор скорости, то есть способна изменять направление движения заряженных частиц. Она перпендикулярна вектору скорости движущейся частицы. Необходимым условием возникновения этой силы является движение электрического заряда.
Для силы Лоренца правило левой руки формулируется следующим образом.
Если четыре вытянутых пальца левой руки указывают направление движения положительного заряда, а линии магнитного поля входят в ладонь, «прокалывая» ее, то отставленный большой палец покажет направление силы Лоренца.
Движение заряженных частиц в магнитном поле (примеры: движение заряженной частицы в однородном поле по окружности и винтовой линии).
Частица массы m, имеющая заряд q > 0, влетает со скоростью в область пространства, где имеется однородное магнитное поле с индукцией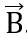 . Угол между и
. Угол между и 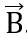 равен α. По какой траектории будет двигаться частица? Запишем II закон Ньютона для данной частицы
равен α. По какой траектории будет двигаться частица? Запишем II закон Ньютона для данной частицы
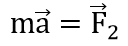
где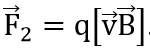 . Сила
. Сила 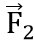 и ускорение
и ускорение 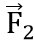 изображены на рисунке в разных проекциях.
изображены на рисунке в разных проекциях.
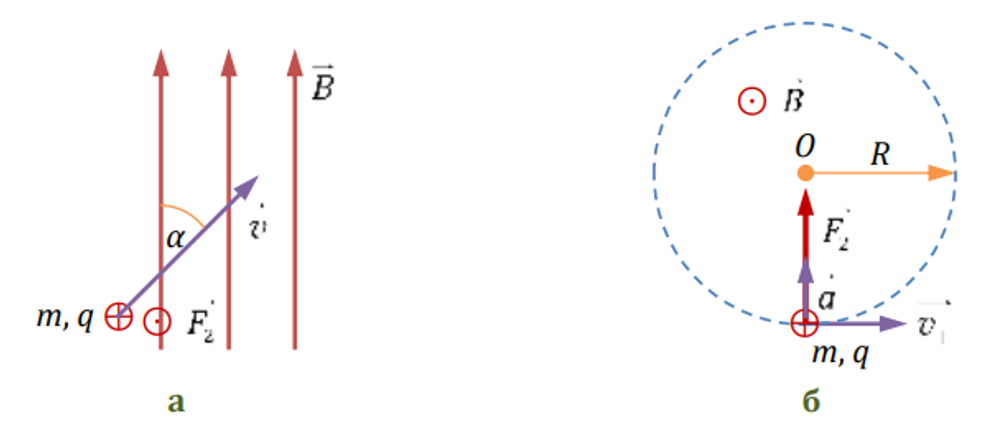
Сила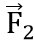 перпендикулярна скорости частицы, так же направлено и ускорение, т. е. a = an — нормальное ускорение. Следовательно, вдоль оси, параллельной линиям магнитной индукции, частица будет двигаться равномерно, а в проекции на плоскость, перпендикулярную линиям магнитной индукции (плоскость рисунка б) — по окружности.
перпендикулярна скорости частицы, так же направлено и ускорение, т. е. a = an — нормальное ускорение. Следовательно, вдоль оси, параллельной линиям магнитной индукции, частица будет двигаться равномерно, а в проекции на плоскость, перпендикулярную линиям магнитной индукции (плоскость рисунка б) — по окружности.
Спроецируем векторное равенство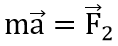 на нормаль к проекции траектории частицы на плоскость, перпендикулярную линиям магнитной индукции:
на нормаль к проекции траектории частицы на плоскость, перпендикулярную линиям магнитной индукции:
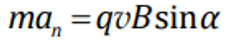
По известной формуле кинематики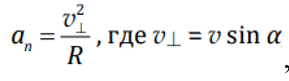 , R — радиус траектории;
, R — радиус траектории;
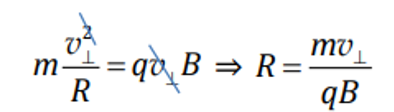
Магнитный поток – поток вектора магнитной индукции. Для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. В этом понятии объединяются все величины, от которых зависит наведенная в рамке ЭДС – индукция поля, площадь и ориентация рамки. Для обозначения используется большая греческая буква Ф (фи):
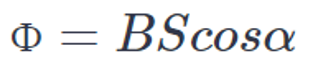
Таким образом, магнитный поток – это величина, равная произведению индукции магнитного поля, площади проводящего контура, и косинуса угла между нормалью к контуру и направлением линий индукции.
Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её.
А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.
Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 108 мкс. Соответственно 1 мкс = 10-8 вб.
Магнитный поток является скалярной величиной.
Работа по перемещению проводника и контура с током в магнитном поле.
На проводник с током в магнитном поле действуют силы, определяемые законом Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током.
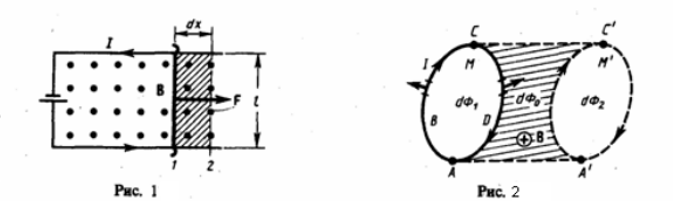
Элементарная работа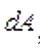 , совершаемая силой Ампера
, совершаемая силой Ампера 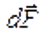 при малом перемещении
при малом перемещении 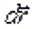 в постоянном магнитном поле малого элемента
в постоянном магнитном поле малого элемента 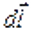 проводника с током
проводника с током 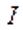 , равна
, равна 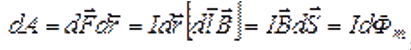 , где
, где 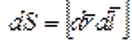 вектор малой площадки, прочерчиваемый элементом
вектор малой площадки, прочерчиваемый элементом 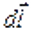 проводника при его малом перемещении
проводника при его малом перемещении 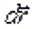 (см. рис.), а
(см. рис.), а 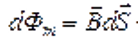 магнитный поток сквозь эту площадку.
магнитный поток сквозь эту площадку.
Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником: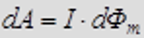 , где
, где 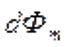 – поток вектора магнитной индукции, пронизывающий площадь, пересекаемую проводником в магнитном поле.
– поток вектора магнитной индукции, пронизывающий площадь, пересекаемую проводником в магнитном поле.
При малом перемещении в магнитном поле проводника конечной длины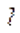 магнитный поток сквозь поверхность, которую прочерчивает весь проводник при его малом перемещении:
магнитный поток сквозь поверхность, которую прочерчивает весь проводник при его малом перемещении:
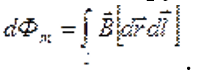 .
.
Если сила тока постоянна и проводник совершил перемещение из положения 1 в положение 2, то работа сил Ампера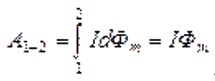 .
.
Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока на изменение магнитного потока: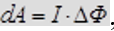 , где
, где 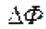 изменение магнитного потока, сцепленного с контуром или магнитный поток через поверхность, прочерченную контуром. Формула справедлива для контура любой формы в произвольном магнитном поле.
изменение магнитного потока, сцепленного с контуром или магнитный поток через поверхность, прочерченную контуром. Формула справедлива для контура любой формы в произвольном магнитном поле.
Замечание. Когда в задаче рассматривается замкнутый контур, находящийся в магнитном поле, то различают два случая:
1) магнитное поле однородно. Тогда на контур с током действует вращающий момент, определяемый формулой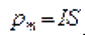 . Под влиянием этого момента контур поворачивается так, что угол
. Под влиянием этого момента контур поворачивается так, что угол 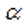 между векторами
между векторами 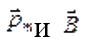 и
и 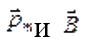 уменьшается. При
уменьшается. При 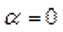 наступает состояние устойчивого равновесия контура в магнитном поле;
наступает состояние устойчивого равновесия контура в магнитном поле;
2) магнитное поле неоднородно. В этом случае на контур с током кроме вращающего момента действует сила, определяемая формулой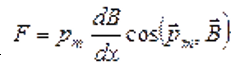 , где
, где 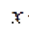 направление быстрейшего изменения величины
направление быстрейшего изменения величины 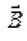 .
.
Эта формула справедлива, если:
- магнитное поле таково, что направления оси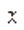 и вектора
и вектора 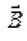 совпадают (например, поле соленоида в точках, лежащих на его оси вблизи концов соленоида);
совпадают (например, поле соленоида в точках, лежащих на его оси вблизи концов соленоида);
- контур с током достаточно мал для того, чтобы во всех точках ограниченной им плоскости можно было считать величину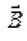 приблизительно одинаковой.
приблизительно одинаковой.
Явление электромагнитной индукции – явление возникновения электрического поля в замкнутом контуре при изменении магнитного потока сквозь поверхность, натянутую на этот контур. В замкнутом проводнике, магнитный поток сквозь который (поверхность, ограниченную которым) изменяется, возникает индукционный ток (возникает только при изменении линий магнитной индукции). Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Для создания тока в цепи необходимо наличие электродвижущей силы. Поэтому явление электромагнитной индукции свидетельствует о том, что при изменении магнитного потока в контуре возникает электродвижущая сила индукции.
ЭДС индукции при движении проводника в магнитном поле.
ЭДС индукции – энергетическая характеристика этого поля.
Рассмотрим движущийся в однородном магнитном поле проводник. В нём на каждый заряд действует сила Лоренца. Под её действием внутри проводника начинают двигаться свободные заряды, из-за чего появляется электродвижущая сила. Эта сила имеет магнитное происхождение и является сторонней. Если в однородном магнитном поле находится контур, состоящий из рамки и движущегося по ней проводника (скорость проводника постоянна и равна V), то сила Лоренца, которая действует на каждую частицу в движущемся проводнике, равна:
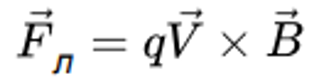 (1)
(1)
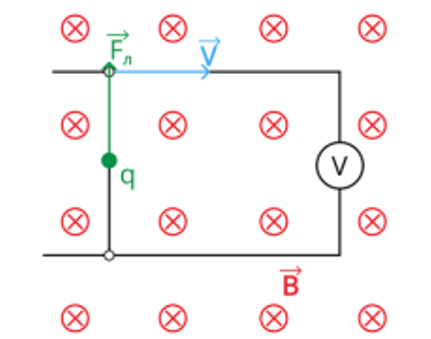
Рисунок. Физическая модель движения проводника в магнитном поле
Формула (1) описывает силу, которая действует на положительный заряд. Она направлена вдоль проводника, а её работа по перемещению заряда между концами этого проводника равна:
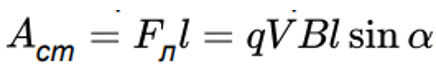 (2)
(2)
Где l — это длина движущегося проводника,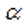 — это угол между вектором индукции магнитного поля и вектором скорости проводника. Из формулы (2) следует формула для ЭДС:
— это угол между вектором индукции магнитного поля и вектором скорости проводника. Из формулы (2) следует формула для ЭДС:
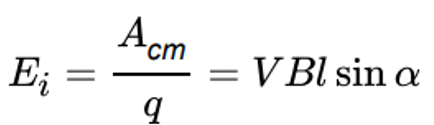
Эту же формулу можно получить из другого типа рассуждений. Рассмотрим этот же эксперимент, однако положим, что движущийся проводник и рамка создают замкнутый контур с некоторой площадью S. За некоторое время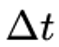 площадь изменится на:
площадь изменится на:
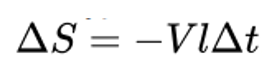
где знак «-» указывает на уменьшение площади. Как следствие, изменится магнитный поток через рассматриваемый контур:
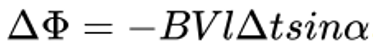
По закону электромагнитной индукции величина возникающей ЭДС может быть определена как:
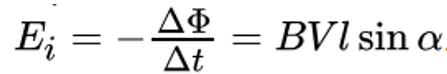
Закон Фарадея-Максвелла (Закон электромагнитной индукции) – закон, устанавливающий взаимосвязь между магнитными и электрическими явлениями. ЭДС электромагнитной индукции, в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
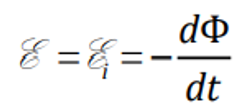
Где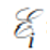 — ЭДС индукции
— ЭДС индукции
Всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции.
Знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем, как знак потока магнитной индукции, так и направление тока и ЭДС в контуре.
При движении замкнутого проводящего контура во внешнем магнитном поле в нем возникает ЭДС индукции, равная скорости изменения магнитного потока через площадь поверхности, ограниченной контуром. Полученный вывод и соотношение выражают основной закон электромагнитной индукции, названный законом Фарадея–Максвелла. Знак “–“ в соотношении показывает, что индукционный ток, возникающий в контуре, своим магнитным полем компенсирует изменение магнитного потока, вызвавшего появление индукционного тока.
Правило Ленца – направление индукционного тока таково, чтобы компенсировать вызвавшее индукционный ток изменение магнитного потока. Правило Ленца выражается знаком «–» в выражении закона Фарадея-Максвелла.
Применение правила Ленца для определения направления индукционного тока предусматривает следующие шаги.
Явление самоиндукции и взаимной индукции.
Самоиндукция — частный случай явления электромагнитной индукции в цепи, по которой уже идет ток. Возникновение электрического поля в замкнутой цепи в результате изменения силы тока в этой цепи.
Φ = LI
Коэффициент пропорциональности L называется индуктивностью контура (коэффициентом самоиндукции).
Направление тока самоиндукции определяется по правилу Ленца: ток самоиндукции всегда направлен так, что он противодействует изменению основного тока. Если основной ток возрастает, то ток самоиндукции направлен против направления основного тока, если уменьшается, то направления основного тока и тока самоиндукции совпадают.
При замыкании ключа ток в цепи нарастает, поэтому индукционный ток имеет противоположное направление. При размыкании ключа ток убывает, следовательно, индукционный ток имеет то же направление, то есть поддерживает внешний ток. Значения токов складываются и может наблюдаться повышение суммарного тока по сравнению с номинальным.
Взаимная индукция — частный случай явления электромагнитной индукции — возникновение электрического поля в проводнике под действием переменного тока в другом проводнике, близко расположенным к данному проводнику. Измеряется она в тех же единицах, что и индуктивность — Генри (Гн).

Индуктивность – характеристика проводника, равная отношению собственного магнитного потока (потокосцепления) к току в проводнике.
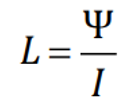
[L] = Гн (генри)
Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды и не зависит от силы тока, магнитной индукции и других характеристик поля и тока (в случае, если нет ферромагнитного сердечника.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:
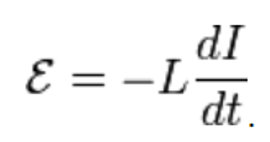
Взаимная индуктивность – величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура (1 и 2, см. рис.), то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).
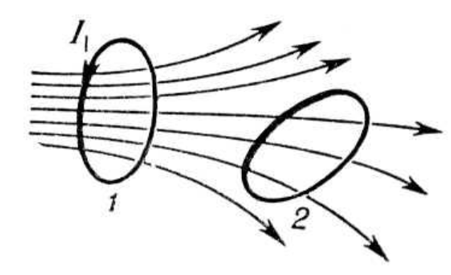
Магнитный поток Ф12 через контур 2, созданный током I1 в контуре 1, прямо пропорционален току:
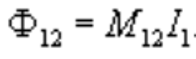 (1)
(1)
Коэффициент пропорциональности M12 зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ измеряется в Генри.
Если ток I2 течёт в контуре 2, то магнитный поток Ф12 через площадь контура 1 также пропорционален току:
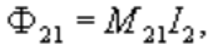 (2)
(2)
причём M21 = M12.
Наличие магнитной связи между контурами проявляется в том, что при изменении тока в одном из контуров появляется эдс индукции в соседнем контуре. Согласно закону индукции электромагнитной (См. Индукция электромагнитная),
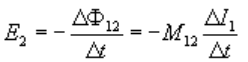
(3)
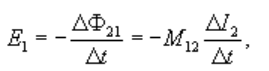
где E2 и E1 — возникающие в контурах 2 и 1 эдс индукции, а ΔФ12 и Δ Ф21
Изменение магнитных потоков через соответствующие контуры за время Δt.
Через w выражается взаимная энергия W12 магнитного поля токов I1 и I2:
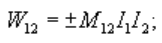 (4)
(4)
знак в (4) зависит от направления токов.
Энергия магнитного поля контура с током.
Вокруг проводника с токомсуществует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в электрическая цепь, обладает запасом энергии. В момент замыкания электрической цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля. Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
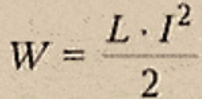
Где L — индуктивность катушки (Гн), I — сила тока в катушке (А).
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? - выделяется (при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
Проводник с током создает вокруг себя магнитное поле, в это поле помещается второй проводник с током, а значит на него будет действовать сила Ампера. Направление силы Ампера зависит от направления линий индукции магнитного поля, которое в свою очередь зависит от направления тока в проводнике.

Закон Ампера – показывает, с какой силой действует магнитное поле на помещенный в него проводник:
Сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.:
где α — угол между векторами магнитной индукции и тока,
B — индукция магнитного поля,
I — сила тока в проводнике,
L — длина проводника.
Этой формулой можно пользоваться:
если длина проводника такая, что индукция во всех точках проводника может считаться одинаковой;
если магнитное поле однородное (тогда длина проводника может быть любой, но при этом проводник целиком должен находиться в поле).
Если проводник имеет произвольную формулу и поле неоднородно, то Закон Ампера принимает вид:
где dF — сила, с которой магнитное поле действует на бесконечно малый проводник с током I,
dl — элемент длины проводника.
К
 онтур с током в магнитном поле.
онтур с током в магнитном поле. Пусть в однородное магнитное поле помещена рамка с током. Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором
Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать
Магнитный момент контура с током.
Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Магнитный момент контура с током величина векторная. Он направлен по нормали к плоскости контура и связан с направлением тока правилом буравчика. Магнитный момент имеет общее значение и определяется выражением

Вращательный момент – физическая величина, характеризующая вращательное действие силы на твёрдое тело.
При помещении контура с током во внешнее однородное магнитное поле на каждый элемент контура
Вращательный момент контура с током можно записать
Действие магнитного поля на движущийся заряд.
На движущийся в магнитном поле заряд (q) со стороны магнитного поля действует сила (F), направление которой зависит от взаимного направления вектора скорости движения (v) заряда и вектора магнитной индукции поля (В). Величина силы пропорциональна скорости движения заряда и модулю магнитной индукции.
Магнитная составляющая электромагнитного поля действует на точечный заряд q, движущийся со скоростью , с силой
— сила Лоренца (магнитная составляющая). Направление этой силы определяют по правилу левой руки.
Сила Лоренца – сила, которая действует со стороны электромагнитного поля на движущийся электрический заряд. Весьма нередко силой Лоренца называют лишь магнитную составляющую этого поля. Формула для определения:
где q — заряд частицы; Е — напряжённость электрического поля; B — магнитная индукция поля; v — скорость частицы.
Она характеризуется тем, что не изменяет скорость перемещения зарядов, а лишь воздействует на вектор скорости, то есть способна изменять направление движения заряженных частиц. Она перпендикулярна вектору скорости движущейся частицы. Необходимым условием возникновения этой силы является движение электрического заряда.
Для силы Лоренца правило левой руки формулируется следующим образом.
Если четыре вытянутых пальца левой руки указывают направление движения положительного заряда, а линии магнитного поля входят в ладонь, «прокалывая» ее, то отставленный большой палец покажет направление силы Лоренца.
Движение заряженных частиц в магнитном поле (примеры: движение заряженной частицы в однородном поле по окружности и винтовой линии).
Частица массы m, имеющая заряд q > 0, влетает со скоростью в область пространства, где имеется однородное магнитное поле с индукцией
где

Сила
Спроецируем векторное равенство
По известной формуле кинематики
Магнитный поток – поток вектора магнитной индукции. Для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. В этом понятии объединяются все величины, от которых зависит наведенная в рамке ЭДС – индукция поля, площадь и ориентация рамки. Для обозначения используется большая греческая буква Ф (фи):
Таким образом, магнитный поток – это величина, равная произведению индукции магнитного поля, площади проводящего контура, и косинуса угла между нормалью к контуру и направлением линий индукции.
Из формулы магнитного потока видно, что максимальным магнитный поток будет при cos α = 1, а это случится, когда вектор B параллелен нормали к поверхности S. Минимальным магнитный поток будет при cos α = 0, это будет, когда вектор B перпендикулярен нормали к поверхности S, ведь в этом случае линии вектора B будут скользить по поверхности S, не пересекая её.
А по определению магнитного потока учитываются только те линии вектора магнитной индукции, которые пересекают данную поверхность.
Измеряется магнитный поток в веберах (вольт-секундах): 1 вб = 1 в * с. Кроме того, для измерения магнитного потока применяют максвелл: 1 вб = 108 мкс. Соответственно 1 мкс = 10-8 вб.
Магнитный поток является скалярной величиной.
Работа по перемещению проводника и контура с током в магнитном поле.
На проводник с током в магнитном поле действуют силы, определяемые законом Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током.

Элементарная работа
Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником:
При малом перемещении в магнитном поле проводника конечной длины
Если сила тока постоянна и проводник совершил перемещение из положения 1 в положение 2, то работа сил Ампера
Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока на изменение магнитного потока:
Замечание. Когда в задаче рассматривается замкнутый контур, находящийся в магнитном поле, то различают два случая:
1) магнитное поле однородно. Тогда на контур с током действует вращающий момент, определяемый формулой
2) магнитное поле неоднородно. В этом случае на контур с током кроме вращающего момента действует сила, определяемая формулой
Эта формула справедлива, если:
- магнитное поле таково, что направления оси
- контур с током достаточно мал для того, чтобы во всех точках ограниченной им плоскости можно было считать величину
Явление электромагнитной индукции – явление возникновения электрического поля в замкнутом контуре при изменении магнитного потока сквозь поверхность, натянутую на этот контур. В замкнутом проводнике, магнитный поток сквозь который (поверхность, ограниченную которым) изменяется, возникает индукционный ток (возникает только при изменении линий магнитной индукции). Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Для создания тока в цепи необходимо наличие электродвижущей силы. Поэтому явление электромагнитной индукции свидетельствует о том, что при изменении магнитного потока в контуре возникает электродвижущая сила индукции.
ЭДС индукции при движении проводника в магнитном поле.
ЭДС индукции – энергетическая характеристика этого поля.
Рассмотрим движущийся в однородном магнитном поле проводник. В нём на каждый заряд действует сила Лоренца. Под её действием внутри проводника начинают двигаться свободные заряды, из-за чего появляется электродвижущая сила. Эта сила имеет магнитное происхождение и является сторонней. Если в однородном магнитном поле находится контур, состоящий из рамки и движущегося по ней проводника (скорость проводника постоянна и равна V), то сила Лоренца, которая действует на каждую частицу в движущемся проводнике, равна:
Рисунок. Физическая модель движения проводника в магнитном поле
Формула (1) описывает силу, которая действует на положительный заряд. Она направлена вдоль проводника, а её работа по перемещению заряда между концами этого проводника равна:
Где l — это длина движущегося проводника,
Эту же формулу можно получить из другого типа рассуждений. Рассмотрим этот же эксперимент, однако положим, что движущийся проводник и рамка создают замкнутый контур с некоторой площадью S. За некоторое время
где знак «-» указывает на уменьшение площади. Как следствие, изменится магнитный поток через рассматриваемый контур:
По закону электромагнитной индукции величина возникающей ЭДС может быть определена как:
Закон Фарадея-Максвелла (Закон электромагнитной индукции) – закон, устанавливающий взаимосвязь между магнитными и электрическими явлениями. ЭДС электромагнитной индукции, в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром.
Где
Всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции.
Знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали определяется правилом правого винта. Следовательно, выбирая положительное направление нормали, мы определяем, как знак потока магнитной индукции, так и направление тока и ЭДС в контуре.
При движении замкнутого проводящего контура во внешнем магнитном поле в нем возникает ЭДС индукции, равная скорости изменения магнитного потока через площадь поверхности, ограниченной контуром. Полученный вывод и соотношение выражают основной закон электромагнитной индукции, названный законом Фарадея–Максвелла. Знак “–“ в соотношении показывает, что индукционный ток, возникающий в контуре, своим магнитным полем компенсирует изменение магнитного потока, вызвавшего появление индукционного тока.
Правило Ленца – направление индукционного тока таково, чтобы компенсировать вызвавшее индукционный ток изменение магнитного потока. Правило Ленца выражается знаком «–» в выражении закона Фарадея-Максвелла.
Применение правила Ленца для определения направления индукционного тока предусматривает следующие шаги.
-
Используя формулу магнитного потока Ф=BScosα, определяется, как изменяется магнитный поток через контур – увеличивается ли он или уменьшается. -
Определяются направление возникающей индукции. Оно, согласно правилу Ленца, должно быть направлено так, чтобы противодействовать причине его вызывающей. То есть, если магнитный поток возрастает, то возникающая индукция должна быть направлена против внешней индукции, если поток уменьшается – то вдоль. -
По правилу буравчика или правилу охвата правой руки определяется направление индукционного тока.
Явление самоиндукции и взаимной индукции.
Самоиндукция — частный случай явления электромагнитной индукции в цепи, по которой уже идет ток. Возникновение электрического поля в замкнутой цепи в результате изменения силы тока в этой цепи.
Φ = LI
Коэффициент пропорциональности L называется индуктивностью контура (коэффициентом самоиндукции).
Направление тока самоиндукции определяется по правилу Ленца: ток самоиндукции всегда направлен так, что он противодействует изменению основного тока. Если основной ток возрастает, то ток самоиндукции направлен против направления основного тока, если уменьшается, то направления основного тока и тока самоиндукции совпадают.
При замыкании ключа ток в цепи нарастает, поэтому индукционный ток имеет противоположное направление. При размыкании ключа ток убывает, следовательно, индукционный ток имеет то же направление, то есть поддерживает внешний ток. Значения токов складываются и может наблюдаться повышение суммарного тока по сравнению с номинальным.
Взаимная индукция — частный случай явления электромагнитной индукции — возникновение электрического поля в проводнике под действием переменного тока в другом проводнике, близко расположенным к данному проводнику. Измеряется она в тех же единицах, что и индуктивность — Генри (Гн).

Индуктивность – характеристика проводника, равная отношению собственного магнитного потока (потокосцепления) к току в проводнике.
[L] = Гн (генри)
Коэффициент самоиндукции L часто называют индуктивностью контура. В СИ индуктивность измеряют в генри (Гн). Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды и не зависит от силы тока, магнитной индукции и других характеристик поля и тока (в случае, если нет ферромагнитного сердечника.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока:
Взаимная индуктивность – величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура (1 и 2, см. рис.), то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).

Магнитный поток Ф12 через контур 2, созданный током I1 в контуре 1, прямо пропорционален току:
Коэффициент пропорциональности M12 зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ измеряется в Генри.
Если ток I2 течёт в контуре 2, то магнитный поток Ф12 через площадь контура 1 также пропорционален току:
причём M21 = M12.
Наличие магнитной связи между контурами проявляется в том, что при изменении тока в одном из контуров появляется эдс индукции в соседнем контуре. Согласно закону индукции электромагнитной (См. Индукция электромагнитная),
(3)
где E2 и E1 — возникающие в контурах 2 и 1 эдс индукции, а ΔФ12 и Δ Ф21
Изменение магнитных потоков через соответствующие контуры за время Δt.
Через w выражается взаимная энергия W12 магнитного поля токов I1 и I2:
знак в (4) зависит от направления токов.
Энергия магнитного поля контура с током.
Вокруг проводника с токомсуществует магнитное поле, которое обладает энергией. Откуда она берется? Источник тока, включенный в электрическая цепь, обладает запасом энергии. В момент замыкания электрической цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля. Энергия магнитного поля равна собственной энергии тока. Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
Где L — индуктивность катушки (Гн), I — сила тока в катушке (А).
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока. Куда пропадает энергия магнитного поля после прекращения тока? - выделяется (при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)