Работа в электрическом поле. Потенциал.

При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна (рисунок ниже):







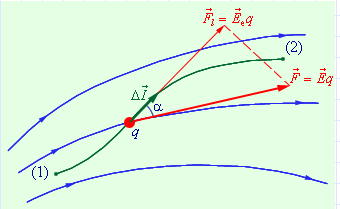
Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.

На рисунке ниже изображены силовые лини кулоновского поля точечного заряда и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое пермещение . Работа кулоновских сил на этом перемещении равна:



Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Если это выражение проинтегрировать на интервале от до то можно получить:





Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на риунке, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Электростатическое поле потенциально, кулоновские силы - консервативные, а работа консервативных сил может быть представлена как убыль потенциальной энергии, то есть:

---

Потенциальная энергия точечного заряда в электростатическом поле

Т 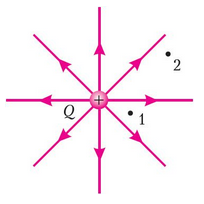очечный электрический заряд, находящийся в любой точке электростатического поля, обладает потенциальной энергией взаимодействия с этим полем. Значение этой энергии определяют относительно произвольно выбираемой нулевой точки. В нулевой точке потенциальную энергию заряда принимают равной нулю. Потенциальная энергия взаимодействия точечного заряда с электростатическим полем равна работе, которую совершила бы сила поля при перемещении данного заряда из указанной точки поля в нулевую точку;

Работа силы поля по перемещению электрического заряда q из точки 1 в точку 2 (рисунок слева) может служить мерой изменения потенциальной энергии этого заряда в поле, созданном зарядом Q.

Пусть и — потенциальные энергии перемещаемого заряда в точках 1 и 2 электростатического поля. Тогда работа силы поля



где — приращение потенциальной энергии заряда q при его перемещении из точки 1 в точку 2.

Перепишем выражение выше в виде



И проанализируем его, когда на заряд q действует только сила со стороны электростатического поля:

1) если работа силы поля (перемещение положительного заряда q происходит в направлении линий напряжённости поля), то потенциальная энергия заряда уменьшается: . При этом, согласно закону сохранения энергии, увеличивается кинетическая энергия тела c зарядом q:

2) если работа силы поля

---

(перемещение положительного заряда противоположно направлению линий напряжённости поля), то потенциальная энергия заряда увеличивается: . При этом кинетическая энергия заряженного тела уменьшается:

3) если работа силы поля (перемещение заряда перпендикулярно направлению линий напряжённости поля), то потенциальная энергия заряда не изменяется.

Следует подчеркнуть, что потенциальная энергия — это энергия взаимодействия, и её необходимо относить не к заряженной частице или телу, а к системе в целом. В частности, для заряженной частицы (тела), находящейся в электростатическом поле, это потенциальная энергия взаимодействия заряженной частицы с полем, т. е. с другими заряженными частицами и (или) телами, являющимися источниками этого поля. Кратко это принято формулировать так: потенциальная энергия заряда в поле.

Потенциал электростатического поля — скалярная энергетическая характеристика электростатического поля, численно равная отношению потенциальной энергии пробного электрического заряда, помещённого в данную точку поля, к величине заряда. Потенциал не зависит от величины заряда, помещенного в это поле.



Напряженность поля является вектором и представляет собой силовую характеристику поля; она определяет силу, действующую на заряд q в данной точке поля. Потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию за­ряда q в данной точке поля.

За единицу потенциала в СИ принят вольт (В). Единица названа в честь итальянского учёного Алессандро Вольта (1745–1827), внёсшего большой вклад в изучение электрических явлений. 1 В — потенциал такой точки электростатического поля, в которой заряд 1 Кл обладал бы потенциальной энергией 1 Дж.

Принцип суперпозиции для потенциала.

Если электрическое поле создается системой неподвижных точечных зарядов q1, q2, … , то согласно принципу наложения электрических полей, результирующее поле равно сумме полей, создаваемых отдельными зарядами. Так как потенциал - это аддитивная скалярная величина, чтобы найти его значение в некотором месте электрических полей, достаточно сложить потенциалы всех полей, действующих на пробный заряд. То есть принцип суперпозиций потенциалов говорит, что общий потенциал в точке равен алгебраической (с учетом знака потенциала) сумме всех потенциалов поля, которое создает в отдельности каждый заряд.

---

Эквипотенциальные поверхности.

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью.

Между двумя любыми точками на эквипотенциальной поверхности разность потенциалов равна нулю, поэтому работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю. Это означает, что вектор силы   в любой точке траектории движения заряда по эквипотенциальной поверхности перпендикулярен вектору скорости. Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальной поверхности. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю. - Источник: Потенциал электрического поля.

Эквипотенциальными поверхностями поля точечного электрического заряда являются сферы, в центре которых расположен заряд (рис. 112).



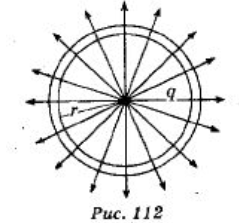
Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности (рис. 113).





Связь между напряженностью поля и потенциалом (интегральная и дифференциальная).

Электростатическое поле имеет две характеристики: силовую (напряжённость) и энергетическую (потенциал). Напряжённость и потенциал – различные характеристики одной и той же точки поля, следовательно, между ними должна быть связь.

Интегральная связь напряжённости и потенциала электростатического поля:





Дифференциальная связь напряжённости и потенциала электростатического поля (определение вектора градиента

---

):



Градиент -вектор, своим направлением указывающий направление наибольшего возрастания некоторой величины , значение которой меняется от одной точки пространства к другой, а по величине (модулю) равный быстроте роста этой величины в этом направлении.

Электростатическое поле в веществе.

При помещении диэлектрика в электрическое поле происходит поляризация диэлектрика. В случае полярных диэлектриков силы, действующие со стороны электрического поля на заряды молекул, создают момент сил, который стремится развернуть молекулу (диполь) вдоль силовых линий поля. В неполярных диэлектриках под действием поля происходит деформация молекул: положительные и отрицательные заряды молекул смещаются в противоположные стороны, и молекулы превращаются в диполи.

В общем случае, при неоднородной поляризации диэлектрика внутри него и на его поверхности появляются связанные заряды. Напряженность электрического поля в любой точке пространства будет являться суперпозицией внешнего поля и поля, создаваемого связанными зарядами.

В образцах, имеющих форму тонкой пластины, шара или тонкого и длинного цилиндра, во внешнем однородном поле будет происходить однородная поляризация. В этом случае связанных объемных зарядов не будет, а возникают только поверхностные связанные заряды. Эти заряды создают электрическое поле, направленное в диэлектрике против внешнего поля, и результирующее поле в диэлектрике ослабляется. Степень ослабления поля зависит как от формы образца, так и от свойств диэлектрика.

Если мы возьмем заряженный плоский конденсатор и полностью заполним его диэлектрической средой (при сохранении зарядов на обкладках конденсатора), то в этом случае отношение напряженности электрического поля в конденсаторе без диэлектрика (в вакууме) к напряженности поля внутри диэлектрика (после заполнения им конденсатора) будет определяться только электрическими свойствами диэлектрика. Величина этого отношения называется диэлектрической проницаемостью и обозначается ε.

Относительная диэлектрическая проницаемость диэлектрика показывает, во сколько раз уменьшается поле в диэлектрике по сравнению с полем в вакууме, созданное одними и теми же внешними источниками:

---

Смотрите также файлы

• 2 Способы анализа и разрешения конфликтов.docx

• Также в России существует ряд особенностей, которые могут оказывать влияние на развитие инновационного предпринимательства.docx

• A. Вы не любите собственного ребенка, вы безответственно относитесь к его воспитанию.pdf

• Иванов Иван Иванович Содержание Содержание 2 Введение 2 Нарушение зрения 4 Способы улучшения зрения 5 Использованная литература.docx

• Практикум.docx