Файл: Динамика основным понятиями в механике являются пространство, время, механическое движение, перемещение Время.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 84
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ДИНАМИКА
Основным понятиями в механике являются пространство , время, механическое движение, перемещение
Время – физическая величина, отражающая свойство материальных процессов иметь определённую продолжительность. абсолютно и однородно.
Пространство – внешняя среда, в которой определяется положение физических тел (вещей), происходит видимое механическое движение, а также геометрическое или умозрительное перемещение различных физических тел и объектов. однородно и изотропно
Изотропность – симметрия в физике, т.е если поменять положение тела на любой другой угол, то это никак не отразится
Однородность – пространство, в котором все точки одинаковы, т.е существует симметрия пространства, переводящая любую точку в другую
Абсолютность – равномерность без отношения к чему-либо внешнему
Механическое движение – изменение положения тела в пространстве относительно других тел с течением времени
Механическая система – совокупность материальных точек, движения которых взаимосвязаны между собой
Система свободных материальных точек – это система, движение которых не ограничено никакими связями
Одна и та же сила может быть как внешней так и внутренней, в зависимости от того, какая система рассматривается. Например, реакции подшипников вала являются внешними силами относительно вала. Эта же реакции относятся к внутренним силам, когда рассматривается вся установка
Материальная точка – тело, имеющее массу, размерами которого можно пренебречь. Одно и то же тело в различных условиях или может считаться материальной точкой, или нет
Абсолютно твёрдое тело – тело, которые не деформируется, взаимное положение точек, форма и распределение масс не меняется при любых процессах
Система отсчёта нужна для расчёта параметров изменения тела в пространстве, она состоит из
Тела отсчёта – тело, относительного которого рассматривается изменение положения других тел в пространстве
Системы координат – числа, способные указать положение выбранной точки в трёхмерном пространстве
Способа измерения времени
Радиус-вектор – вектор, начало которого совпадает с началом системы координат, а конец – с данной точкой. Особенностью радиус-вектора, отличающего от всех других векторов, является то, что его начало всегда находится в точке начала координат
Кинематический закон движения – функция, выражающая положение точки в любой момент времени.
Если точка перемещается, то в любой следующий момент времени координаты изменяются:
r = r(t); Данное уравнение является векторной формой закона. Движение материальной точки полностью определено, если координаты материальной точки заданы в зависимости от времени x = x(t), y= y(t), z=z(t)
Траектория – непрерывная линия, которая описывает материальную точку при движении
В зависимости от траектории движение бывает прямолинейным и криволинейным
Прямолинейное движение – траектория является прямая линия
Криволинейное движение – траектория является кривая линия
Путь – скалярная физическая величина, равная длине траектории, описываемой телом за рассматриваемый промежуток времени. Чаще всего обозначается как S, и в система СИ измеряется в метрах
Или длина участка траектории материальной точки, пройденного ею за определённое время
Перемещение – вектор, которые соединяет начальную точку движения тела с его конечной точкой
Перемещение и путь – разные физические величины
Скорость – векторная физическая величина, характеризующая быстроту перемещения в единицу времени
Ускорение (мгновенным ускорением) – вектор, который определяет быстроту, с которой изменяется скорость перемещающейся материальной точки.
Обозначается буквой a
Равноускоренное движение – движение изменяющееся на одинаковую величину за любые равные промежутки времени
Равномерное движение – движение, при котором тело за любые равные промежутки времени совершает одинаковое перемещение или проходит одинаковый путь
Радиус кривизны траектории – окружность, вписанная в апроксимации (приближение масштаба позиции) ускорения, т.е ускорение, которое идёт по данной окружности
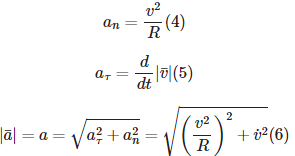 , где
, где Кривизна траектории – величина, обратная радиусы кривизны
Нормальное ускорение – ускорение, в котором тело движется по дуге окружности с центростремительным ускорением, которое направлено перпендикулярно траектории. Это ускорение, которое имеет только одну компоненту (центростр ускорение), величины не меняются
Тангенциальное ускорение – ускорение, которое имеет дополнительную компоненту (тангенсыальная компонента). Величина ускорения – отношению приращения модуля скорости ко времени. Если тело ускоряется, то тело смотрит в направлении его скорости и увеличивают эту скорости и наоборот.

Законы Ньютона
Первый закон Ньютона (ссылка)
Если на тело не действуют силы или их действие скомпенсировано, то данное тело находится в состоянии покоя или равномерного прямолинейного движения.
Существуют системы отсчета, называемые инерциальными (ИСО), в которых тело находится в состоянии покоя (V = 0) или движется равномерно и прямолинейно (V = const), если на тело не действуют силы (F = 0) или действие этих сил скомпенсировано (F = 0).
Свойство тел сохранять свою скорость при отсутствии действия на него других тел называется инерцией. Масса тела – количественная мера его инертности. В СИ она измеряется в килограммах.
Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными. Системы отсчета, движущиеся относительно инерциальных с ускорением, называются неинерциальными
Инерциальные системы отсчёта обладают следующими свойствами
Тела в таких системах движутся равномерно или находятся в состояния покоя
При одинаковых начальных условиях тела движутся одинаково
Изменение скорости тела происходит в результате действия на него других тел
Равнодействующая сила – векторная сумма всех сил, действующих на тело. При равномерном прямолинейном движении или в состоянии покоя равнодействующая сила равна нулю
Второй закон Ньютона
В ИСО ускорение, с которым движется тело, прямо пропорционально равнодействующей всех сил и обратно пропорционально массе этого тела.
| | | |
Сила и ускорение — величины векторные, их направления всегда совпадают
Вспомним Соню в поезде метро. Рассмотрим участок разгона электропоезда под действием равнодействующей силы. Согласно 2-му закону Ньютона, чем больше равнодействующая сила, тем большее ускорение приобретет поезд. Под действием той же силы более легкий поезд будет двигаться с бóльшим ускорением.
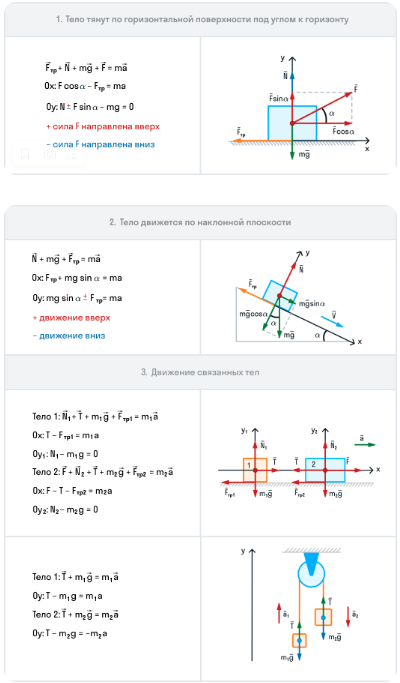
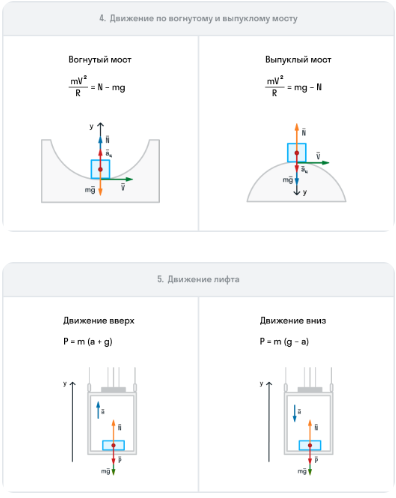
Алгоритм решения задач с использованием 2го закона Ньютона
Выбрать ИСО.
Отметить на рисунке все силы, действующие на тело.
Записать 2-й закон Ньютона в векторном виде.
Найти проекции сил на координатные оси.
Записать 2-й закон Ньютона в проекциях на координатные оси.
Составить и решить систему уравнений.
Выполнить расчет и записать ответ.
Третий закон Ньютона
Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:
Тела действуют друг на друга с силами, направленными вдоль одной прямой, противоположными по направлению и разными по модулю.
Суть закона в том, что сила действия равна силе противодействия. Причем силы имеют одну природу, а приложены они к разным телам.

Сила
Сила — векторная физическая величина, которая является мерой воздействия на данное тело со стороны других тел или полей.
Сила обозначается латинской буквой F, а измеряется в ньютонах [H]
1 Н = 1 кг · м/с2. Измерение силы – динамометр. ВЕКТОРНА
Пользуясь понятием силы, в механике обычно говорят о движении и деформации рассматриваемого тела под действием приложенных к нему сил. При этом, конечно, каждой силе соответствует какое-то определенное тело или поле, действующее с этой силой
Сила F полностью задана, если указаны её
Модуль F
Направление в пространстве и точка приложения
Прямая, вдоль которой направлена сила, называется линией действия силы
Центральными называются силы, которые всюду направлены вдоль прямых, проходящих через одну и ту же неподвижную точку – центр сил, и зависят только от расстояния до центра сил
Если поле, действующее на материалтьную точку с силой F, не изменяется с течением времени, оно называется стационарным полем
Одновременное действие на материальную точку нескольких сил эквивалетно действию одной силы, называемой равнодействующей (результирующей) силой F и равной их геометрической сумме
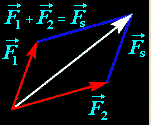
Принцип независимости действия сил означает, что две или более силы действуют независимо друг от друга, не влияя на другие силы. Например, если приложить две силы к одному и тому же объекту, каждая сила будет действовать независимо и не будет влиять на другую силу. Таким образом, результатом действия двух сил будет их сумма.
Деформация – изменение формы и размеров тела (или части тела) под действием внешних сил
Виды деформации:
-
Деформация растяжения -
Сжатия -
Сдвига -
При кручении -
При изгибе
Сила упругости, закон Гука (ссылка)
Если при ударе объекта деформации не будет совсем, то он будет называться абсолютным упругим.
Если объект наоборот полностью деформируется, то он будет абсолютно неупругим.
При деформации возникает сила упругости – сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональная абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука

Принцип независимости действия сил или принцип суперпозиции – силы в механике подчиняются принципу суперпозиции. Если на материаоьное действуют несколько сил, то результирующая из выражения
Инерциальные системы отсчёта (ссылка)– система отсчёта, в которой тела либу движутся прямолинейно и равномерно, либо покоятся
Неинерциальными называют системы отсчёта, в которых закон инцерции не выполняется. Одно и то же тело может находиться в состоянии покоя в одной симстеме отсчёта и двигаться с ускорением в другой системе отсчёта
В самолёте, пикирующем вниз с ускорением свободного падения, пилот находится в состоянии покоя в системе отсчета, связанной с Землёй, этот пилот движется вместе с самолётом с ускорением свободного падения
Инертность – свойство тела сохранять свою скорость постоянной ( то же, что и инерция). Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным
Мера инертности – масса.
Чем инертнее тело, тем боле его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение.
Измерение массы методом взаимодействия тел
Два тела, скрепленённые между собой сжатой пружиной, после пережигания нити, удерживающей пружину, начинают двигаться некоторое время с ускорением. Опыт показывает, что при любых взаимодействиях данных двух тел, отношение ускорений тел равно обратному отношению их масс:
| | 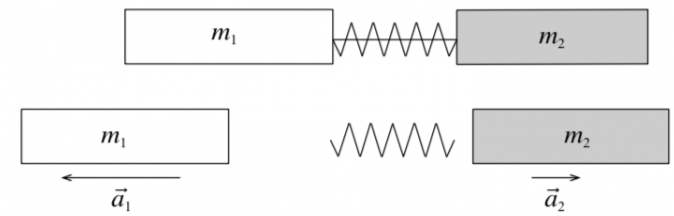 |
Масса, измеренная путём взаимодействия (измерения ускорения), называется инертной
Измерение массы методом взвешивания тел
Второй способ измерения масс основан на сравнении действия Земли на различные тела. Такое сравнение можно осуществить либо последовательно (сначала определяют растяжение пружины под действием эталонных масс, а потом под действием исследуемого тела в тех же условиях), либо одновременно располагают на равноплечих рычажных весах на одной чаше исследуемое тело, а на другой эталонные массы
Масса – скалярная физическая величина, которая овляется мерой инерционных его свойств и источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной
Это аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равно сумме масс всех отдельных частей системы (mi)
Масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела
Выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени
Существует несколько типов массы
Инертная
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона
Гравитационная
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки, при этом она носит название гравитационной (тяжёлой) массы
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой тяжести избранного тела
Гравитационная сила (закон всемирного тяготения) – сила взаимного притяжения двух тело прямо пропорциональная произведения масс этих тел и обратно пропорциональна квадрату расстояния между ними
Гравитационная сила, с которой Земля притягивает к себе тела, придавая им ускорение свободного падения, называется силой тяжести.
Сила сухого трения – сила, возникающая при соприкосновении двух твёрдых тел при отсутствии между ними жидкой или газообразной прослойки. Они всегда направлены по касательной соприкасающимися поверхностям.
Сухое трение, возникающее при относительном покое тел, называют трением покоя. Сила трения покоя всегда равна по величине внешней силе и направлена в противоположную сторону
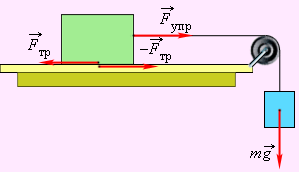
Сила трения покоя
Сила трения покоя не может превышать некоторого максимального значения (Fтр)max. Если внешняя сила больше (Fтр)max, возникает относительное проскальзывание. Силу трения в этом случае называют силой трения скольжения. Она всегда направлена в сторону, противоположную направлению движения и, вообще говоря, зависит от относительной скорости тел. Однако, во многих случаях приближенно силу трения скольжения можно считтьта независящей от величины относительной скорости тел и равно максимальной силе трения покоя.
Опыт показывает, что сила трения сколжения пропорциональная силе нормального давления тела на опору, а следовательно, и силе реакции опоры
Коэффицент пропорциональности u называется коэффицент трения меньше единицы. Он зависит от материалов соприкасающихся тел и от качества обработки поверзностей. При скольжении сила трения направлена по касательной к соприксающимся поверхностям в сторону, противоположную относительной скорости
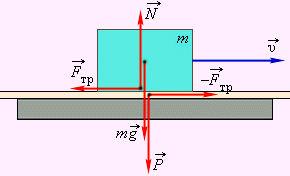
При движении твердого тела в жидкости или газе возникает сила вязкого трения. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя.
Импульс тела (материальной точки) – векторная величина, равная произведения массы тела на скорость тела:
Направление импульса тела всегда совпадает с направлением скорости, тк m > 0:
Единица измерения импульса:
Импульс силы – произведение силы на время её действия:
Направления
2й закона Ньютона в импульсной форме: изменение импульса тела (мт) равно импульсу силы, действующей на него
Импульс тела равен сумме импульсов отдельных элементов
Импульс системы тел равен векторной сумме импульсов каждого из тел системы
Закон сохранения (изменения) импульса системы материальных точек
Найдём скорость
По третьему закону Ньютона
Из приведённого доказательства следует, что третий закон Ньютона можно сформулировать и как требования сохранения импульса системы взаимодействующих тел, если нет никаких других внешних сил
Масса M механической системы равна арифметической сумме масс всех точек или тел, образующих систему
Центром масс механической системы называют геометрическую точку С, радиус-векторой которой определяется с помощью формулы
Проецируя равенство на координатные оси, получаем формулы для координат центра масс системы:
Центр масс системы является не материальной точкой, а геометрической
Внутренние силы -
Внешние силы -
Теорема о движении центра масс механической системы
Центр масс механической системы движется как материальная точка с массой, равной массе системы, под действием главного вектора внешних сил, действующих на эту механическую систему
Выделим условно из механической системы некоторую материальную точку. Mj(mj), на которую будут действовать две силы:
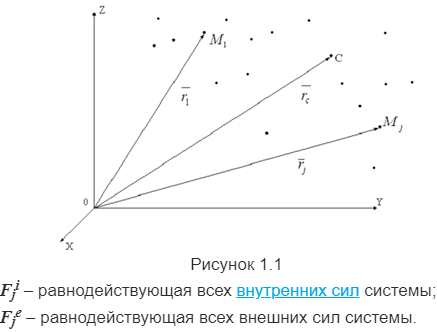
Рассматривая выделенную точку как свободную, запишем для неё дифференциальное уравнение в векторной форме:
Составим аналогичным образом уравнения для всхе точек системы (j=1,2,3,...,n) и формально их просуммируем:
Рассмотрим суммы, стоящие в правой части равенства

Преобразуем левую часть равенства
В результате уравнение принимает вид
Таким образом теорема формулируется так: центр масс механической системы движется как материальная точка с массой, равной массе системы, под действием главного вектора внешних сил, действующих на эту механическую систему
Проецируя векторное равенство на неподвижные оси декартовых координат, получаем три дифференциальных уравнения движения центра масс
Рассмотрим следствия из теоремы о движении центра масс, вытекающие из формул (1.8) и (1.10)
-
Если главный вектор внешних сил, действующих на механическую систему, равен нулю, т.е. Re = ∑Fje = 0, то ac= 0 или Vc= const. При этом, если в начальный момент центр масс механической системы был в покое (Vc= 0), то и в дальнейшем центр масс остается неподвижным (rc= const); -
Если проекция на какую-либо ось (например на ось Ox) главного вектора внешних сил, действующих на механическую систему, равна нулю, т.е. Rxe = ∑Xje = 0, то acx = 0 или Vcx = const, т.е. имеем закон сохранения проекции скорости центра масс: если проекция главного вектора (алгебраическая сумма проекций) всех действующих на механическую систему внешних сил на какую-либо неподвижную ось равна нулю, то проекция скорости центра масс на эту же ось остается постоянной.
В частности, если в начальный момент Vcx = 0, то и в последующие моменты Vcx = 0 и, следовательно, xc = const, т.е. центр масс системы в этом случае вдоль оси Ox не перемещается.
Работа силы
Механическая работа – физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А
 , cosa – добавляется при наличия угла между величинами
, cosa – добавляется при наличия угла между величинамиЧисловое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей
Для совершения работы необходимы два условия
-
Чтобы на тело действовала сила -
Чтобы происходило перемещение тела
Работа равна нули, если
-
При приложенной силе перемещение отсутствует -
Сила не приложена и тело перемещает по инерции -
Угол между векторами силы и перемещения равен 90 градусов
Кинетическая энергия материальной точки
Это скалярная положительная величина, равная половине произведения массы точки на квадрат её скорости
Если тело находится в состоянии покоя, его кинетическая энергия равна нулю
Кинетическая энергия тела (E кин) зависит от массы тела (m) и от скорости его движения (v)
Кинетическая энергия прямо пропорциональная массе тела и квадрату его скорости
Определяют кинетическую энергию по формуле
Чтобы рассчитать массу или скорость, формулу преобразуют следующим образом
С увеличением массы тела в линейной зависимости увеличивается также и его кинетическая энергия. Если масса увеличивается в 2 раза, тогда кинетическая энергия увеличивается также в 2 раза. С увеличением скорости движения тела увеличивается также и его кинетическая энергия в квадратичной зависимости. Если скорость увеличивается в 2 раза, тогда кинетическая энергия увеличивается в 4 раза
Теорема об изменение кинетической энергии
Работа силы или равнодействующей всех сил равна изменению кинетической энергии тела
Когда сила, действующая на тело, направлена в сторону движения тела, и следовательно, совершает положительную работу, то конечная кинетическая энергия больше, чем начальная кинетическая энергия. Этот результат означает, что в данном случае кин эн тела увеличивается. В противоположном случае, когда сила направлена в противоположную сторону скорости, то кинетическая энергия тела должна уменьшаться
Два вывода из теоремы:
Кинетическая энергия измеряется джоулях
Данная теорема основывается на 2 ЗН, это означает, что сама по себе теорема об изменении кин энергии является иначе сформулированным 2 ЗН
Консервативные и неконсервативные силы
Консервативные силы (к-силы) (или потенциальные) (ссылка) - силы, работа которых при перемещении тела от точки 1 к точке 2 зависит не от траектории движения этого между этими точками, а только от положения этих точек.
Если тело движется перпендикулярно направлению силы, работа равна нулю, а если противоположно – работа получается отрицательной. Это значит, что если тело, на которое действует сила, переместилось по прямой сперва в одну сторону, а потом обратно, вернувшись в исходную точку, суммарная работа сила на этом пути будет равна нулю. Это происходит потому, что направление и модуль силы постоянны и не зависят ни от скорости, ни от ускорения, ни от направления перемещения. Такие силы консервативны
Если работа не зависит от пути, то это означает, что работа по замкнутому контуру равна нулю
К-силы это сила работ которых по замкнутому пути равна нулю
В консервативные силы входят
-
Сила тяжести -
Сила упругости -
Сила гравитации -
Сила электростатического взаимодействия
Неконсервативные силы (диссипативные) – силы, для которых невозможно ввести потнцеальную энергию, следовательно, не имеет смысла говорить о полной механический энергии и её сохраняемости. При действии неконсервативных сил, полная (механическая) энергия не сохраняется.
Примером диссипативной силы является сила трения, её значения при движении тела незменно и равно
Если тело переместилось в одну сторону, а потом вернулось, работа сильы трения будет состоять из двух отрицательных компонент, равных по модулю. Их сумма не будет равна нулю. Таким образхом, сила трения не является консервативной. Чаще всего работа диссипативных сил отрицательна
Потенциальная энергия материальной точки (ссылка)
Потенциальной энергией называют вид механической энергии систем тел, которая определена силами взаимодействия между телами и их взаиморасположением. Она определяется работой, совершаемой потенциальными силами, которые действуют на все части системы, если система переходит из исследуемой конфигурации к состоянию .в котором считают потенциальную энергию равной нулю. Т.е работа консервативных сил равна убыли потенциальных энергии. Начало отсчёта потенциальной энергии делают произвольно. Эмпирически представляется возможным измерение только изменения потенциальной энергии. Начало отсчёта делают так, чтобы упрощалось решение конкретной задачи
Потенциальная энергия является скаляром. Чаще всего потенциальную энергию обозначают Ep
Потенциальную энергию можно разделить на внутреннюю и внешнюю, тогда :
Потенциальная энергия материальной точки находящейся в потенциальном поле сил определяет формулой
Механическая энергия (Полная механическая энергия) (Якласс) (skysmart) (interneturok)
Полная механическая энергия тела равна сумме его кинетической и потенциальной энергии. Полную мех энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остается постоянной.
Закон сохранения энергии – полная механическая энергия замкнутой системы остается постоянной
Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движения, тогда полная механическая энергия тела остаётся неизменной во времени.

Внутренняя энергия – сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. Т.е та энергия, которая запасена у тела за счёт его собственных параметров
Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путём совершения механической работы над телом. Например, если сгибать и разгибать проволоку – она будет нагревать
Закон сохранения механической энергии система материальных точек (закон сохранения механической энергии) (ссылка)
Если система замкнута и силы взаимодействия между частицами консервативны, то полная механическая энергия сохраняется. В основе закона сохранения механической энергии лежит однородность времени, тюе равнозначность всех моментов времени
, где Wk – кинетическая энергия, Wp – потенциальная
Абсолютно упругий удар и не упругий удар (ссылка)
В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временим взаимодействия можно пренебречь
При ударе выполняется закон сохранения импульса
Предполагается, что на время удара действием внешних сил можно пренебречь. Тогда полный импульс тел при ударе сохраняется. В противном случае нужно учитывать импульс внешних сил. Часть энергии обычно уходит на нагрев тела и звук.
Результат столкновения двух тел можно полностью рассчитать, если известно их движение до удара и механическая энергия после удара.
Если не известны потери энергии, происходит одновременное столкновение нескольких тел или столкновение точечных частиц, то определить однозначное движение после удара невозможно.
В общем случае решение задачи о столкновении, кроме знания начальных скоростей требует дополнительных параметров
Абсолютно упругий удар – модель соударения, при которой полная кинетическая энергия системы сохраняется. Хорошим примером упругого удара является столкновение бильярдных шаров или упругих мячико
Математическая модель абсолютно упругого удара работает примерно следующим образом:
-
Есть в наличии два абсолютно твёрдых тела, которые сталкиваются -
В точке контакта происходит упругие деформации. Кинетическая энергия движущихся тел мгновенно и полностью переходит в энергию деформации. -
В следующий момент деформированные тела принимают свою прежнюю форму, а энергия деформации полностью обратно переходит в кинетическую энергию -
Контакт тел прекращается, и они продолжают движение
Для математического описания простейших абсолютно упругих ударов используется закон сохранения энергии
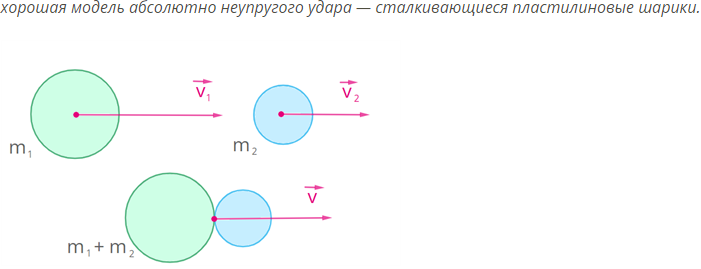
Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело

Импульсы являются величинами векторными, поэтому складываются только векторно
Как и при любом ударе, при абсолютно неупругом ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соударяемых тел в результате неупругих деформаций переходит в тепловую
Электродинамика
Раздел 1.
-
Электрический заряд -
Точечный и распределенный заряд -
Закон Кулона
Поле
Поле - любая изменяющаяся в пространстве физическая величина.
Поле бывает:
-
скалярное (прим. температурное поле ) - изображается изолиниями (поверхностями постоянной величины)
) - изображается изолиниями (поверхностями постоянной величины) -
векторное (прим. гравитационное поле ) - изображается силовыми линиями
) - изображается силовыми линиями
Силовые линии строят так, чтобы их густота была пропорциональна модулю векторного поля.
Электрический заряд. Закон сохранения электрического заряда.
Электрический заряд – квантовое число, характеризующее частицу как источник электромагнитного взаимодействия.
В классической физике электрический заряд - скалярная алгебраическая величина - характеристика электрически заряженного тела, т.е. тела, на которое действует электромагнитное поле.
Элементарный заряд - минимальный (по модулю) электрический заряд частиц, наблюдаемых в свободном состоянии.
Электрический изолированная система - система тел, для которой сумма электрических зарядов частиц, появившихся в этой системе, равна нулю.
Закон сохранения электрического заряда - суммарный электрический заряд любой электрически изолированной системы не изменяется в процессах, происходящих в этой системе:
Линейная плотность электрического заряда - заряд, приходящийся на единичный участок протяженного заряженного тела:
Объемная плотность электрического заряда - заряд, приходящийся на участок заряженного тела единичного объема:
Поверхностная плотность электрического заряда - заряд, приходящийся на единичный участок поверхности заряженного тела:
Электрический заряд тела выражается через плотности заряда следующим образом:
здесь l, S, V - соответственно длина , площадь поверхности и объем заряженного тела.
Электрический ток - упорядоченное движение электрически заряженных частиц.
Точечный и распределенный заряд. Разъяснение написанного выше.
Идеальной физической моделью заряда в электростатике является точечный заряд,
Точечным зарядом называется заряд, сосредоточенный на теле, размерами которого можно пренебречь по сравнению с расстоянием до других тел или до рассматриваемой точки поля. Иными словами, точечный заряд - это материальная точка, которая имеет электрический заряд.
Если заряженное тело настолько велико, что его нельзя рассматривать как точечный заряд, то в этом случае необходимо знать распределение зарядов внутри тел.
Закон Кулона. Расчет напряженности электрического поля методом суперпозиции.
Закон кулона: закон взаимодействия двух точечных зарядов
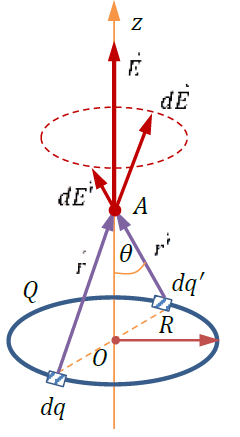
На рисунке ниже заряды q1 и q2 одного знака:
Напряженность электрического поля точечного заряда:
Силовые линии электрического поля точечного заряда представлены на рисунке ниже:
Пример: Электрическое поле равномерно заряженного тонкого кольца
По тонкому кольцу равномерно распределен заряд Q > 0. Найти
Находим напряженность электрического поля в точке А на оси кольца (ОА = z). Разобьем кольцо на точечные заряды dq (на рисунке ниже слева показаны два малых заряда dq и dq’, равные по модулю и расположенные диаметрально противоположно) По принципу суперпозиции полей
,
Вычислим
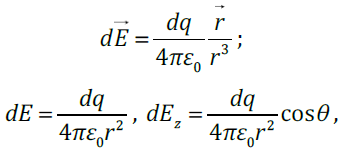
угол
Подставим эти формулы в выражение для
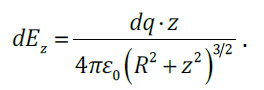
В этом выражении все величины – постоянные, кроме dq. Проинтегрируем по q:
Предельные случаи:
-
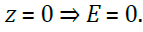
-
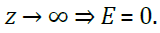
-
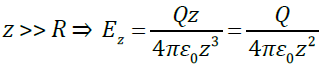 - поле точечного заряда
- поле точечного заряда
Раздел 2.
-
Электростатическое поле -
Вектор напряженности электростатического поля -
Принцип суперпозиции для напряженности -
Работа сил электростатического поля по перемещению заряда -
Потенциальная энергия точечного заряда в электрическом поле -
Потенциал электростатического поля -
Принцип суперпозиции для потенциала -
Эквипотенциальные поверхности -
Связь между напряженностью поля и потенциалом (интегральная и дифференциальная)
Электростатическое поле
Электростатическое поле - поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами. Другими словами, это электрическое поле, создаваемое неизменным во времени распределенным зарядом.
Напряженность электростатического поля - векторная физическая величина, характеризующая электрическое поле в данной точке и равная отношению силы , действующей на неподвижный малый по величине точечный заряд, помещенный в данную точку, к величине этого заряда
Напряженность электрического (электростатического) поля иногда называют силовой характеристикой электрического (электростатического) поля, так как всё отличие от вектора силы, действующей на заряженную частицу, состоит в постоянном множителе. Расшифровывая данное понятие, объясним так. Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или к ней что-то заряженное присоединится.
В каждой точке в данный момент времени существует своё значение вектора (вообще говоря - разное* в разных точках пространства), таким образом, - это векторное поле. Формально оно отражается в записи:
представляющей напряженность электрического поля как функцию пространственных координат (и времени, так как может постоянно меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле, и законы, которым оно подчиняется, суть предмет электродинамики.
*Иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве ( или в какой-то области), говорят об однородном электрическом поле - это частный, наиболее простой, случай электрического поля; в реальности электрическое поле может быть однородным лишь приближённо, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
Напряженность электрического поля в Международной системе единиц (СИ) измеряется в вольтах на метр [В/м] или в ньютонах на кулон [Н/Кл].