Файл: Определение эффективного алгоритма сортировки на основе эмпирического и асимптотического.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 117

Скачиваний: 16

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Практическая работа № 3


Определение эффективного алгоритма сортировки на основе эмпирического и асимптотического методов анализа
Цель: получить навыки по анализу вычислительной сложности алгоритмов сортировки и определению наиболее эффективного алгоритма.
Задание 1. Эмпирическая оценка эффективности алгоритмов Требования по выполнению задания

  1. Разработать алгоритм ускоренной сортировки, определенной в варианте (приложение 1), реализовать код на языке С++. Сформировать таблицу

    1. результатов эмпирической оценки сложности сортировки по фор- мату табл. 1 для массива, заполненного случайными числами1.

  2. Определить ёмкостную сложность алгоритма ускоренной сортировки.



Таблица 1. Сводная таблица результатов


n
T(n), мс
Тп(n)=Cф+Mф

100






1000






10000






100000






1000000






  1. Разработать алгоритм быстрой сортировки, определенной в варианте (приложение 1), реализовать код на языке С++. Сформировать таблицу

1.2 результатов эмпирической оценки сортировки по формату табл. 1 для массива, заполненного случайными числами.

  1. Определить ёмкостную сложность алгоритма быстрой сортировки.

  2. Добавьте в отчёт данные по работе любого из алгоритмов простой сор- тировки в среднем случае, полученные в предыдущей практической ра- боте (в отчёте – таблица 1.3).

  3. Представить на общем сравнительном графике зависимости Тп(n)=Cф+Mф для трёх анализируемых алгоритмов2. График должен быть подписан, на нём – обозначены оси.

  4. На основе сравнения полученных данных определите наиболее эффек- тивный из алгоритмов в среднем случае (отдельно для небольших мас- сивов при n до 1000 и для больших массивов с n>1000).

  5. Провести дополнительные прогоны программ ускоренной и быстрой сортировок на массивах, отсортированных а) строго в убывающем и б) строго возрастающем порядке значений элементов. Заполнить по этим данным соответствующие таблицы 1.4 и 1.5 для каждого алгоритма по формату табл. 1.




1 Для соблюдения равенства условий при анализе эффективности, случайные массивы всех заданных длин должны быть одними и теми же для всех рассматриваемых алгоритмов.

2 Можно разбить график на два: первый – для n до 1000, второй – для n>1000.

  1. Сделайте вывод о зависимости (или независимости) алгоритмов сорти- ровок от исходной упорядоченности массива на основе результатов, представленных в таблицах.


Задание 2. Асимптотический анализ сложности алгоритмов Требования по выполнению задания

  1. Из материалов предыдущей практической работы приведите в отчёте формулы Тт(n) функций роста алгоритма простой сортировки в луч- шем и худшем случае (того же алгоритма, что и в задании 1).

  2. На основе определений соответствующих нотаций получите асимп- тотическую оценку вычислительной сложности простого алгоритма сортировки3:

  • в О-нотации (оценка сверху) для анализа худшего случая;

  • в Ω-нотации (оценка снизу) для анализа лучшего случая.

  1. Получите (если это возможно) асимптотически точную оценку вы- числительной сложности алгоритма в нотации θ.

  2. Реализуйте графическое представление функции роста и полученных асимптотических оценок сверху и снизу.

  3. Привести справочную информацию о вычислительной сложности усовершенствованного и быстрого алгоритмов сортировки, заданных в вашем варианте.

  4. Общие результаты свести в табл. 2.

Таблица 2. Сводная таблица результатов



Алгоритм4
Асимптотическая сложность алгоритма

Наихудший случай (сверху)
Наилучший случай (снизу)
Средний случай (точная оценка)
Ёмкостная сложность

Простой












Усовершен- ствованный












Быстрый












  1. Сделать вывод о наиболее эффективном алгоритме из трёх.

Отчёт


В отчёте по каждой сортировке необходимо привести словесное описание ал- горитма и его блок-схему, а также программный код (с комментариями), ре- зультаты тестирования на массиве n=10 и контрольных прогонов на массивах длиной 100, 1000, 10000, 100000 и 1000000 элементов.

По итогам выполнения каждого задания сформулируйте соответствующие выводы.



3 Здесь математически доказывается существование коэффициентов, при которых истинны лежащие в ос- нове определения каждой нотации неравенства.

4 В отчёте в этом столбце укажите названия соответствующих алгоритмов.

Приложение 1. Варианты индивидуальных заданий.


Вариант
Усовершенствован- ный алгоритм
Быстрый алгоритм

1
Сортировка обменами с условием Айверсона
Простое слияние

2
Шейкерная сортировка
Простое слияние

3
Шейкерная с условием Айверсона
Простое слияние

4
Сортировка Шелла со смещениями Д. Кнута. Способ 1
Простое слияние

5
Шелла со смещениями Д. Кнута. Способ 2
Простое слияние

6
Шелла со смещениями Р. Седжвика.
Простое слияние

7
Пирамидальная сорти-

ровка
Простое слияние

8
Турнирная сортировка
Простое слияние

9
Сортировка обменами с условием Айверсона
Быстрая сортировка (Хоара)

10
Шейкерная сортировка
Быстрая сортировка (Хоара)

11
Шейкерная с условием Айверсона
Быстрая сортировка (Хоара)

12
Сортировка Шелла со

смещениями Д. Кнута. Способ 1
Быстрая сортировка (Хоара)

13
Шелла со смещениями Д. Кнута. Способ 2
Быстрая сортировка (Хоара)

14
Шелла со смещениями Р. Седжвика.
Быстрая сортировка (Хоара)

15
Пирамидальная сорти- ровка
Быстрая сортировка (Хоара)

16
Турнирная сортировка
Быстрая сортировка (Хоара)

Приложение 2. Методы определения смещения для сортировки Шелла, предложенные Д. Кнутом и Р. Седжвиком

Перед выполнением сортировки происходит вычисление длин промежут- ков (значения d из примера сортировки Шелла), которые записываются в мас- сив, например, d.

ПоСеджвику

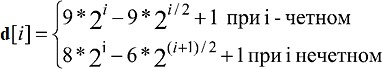Значение смещения, записываемого в элемент массива d, вычисляется по формуле:

Остановить создание и заполнение массива d на значении d[i-1], если 3*d[i] > n (размера массива).

ПоКнуту

Если t – количество смещений, то: Способ 1:

t=log3n-1 d0 =1, d[i-1]=3*d[i]+1 т.е. 1, 4, 13, 40, 121, …..

Способ 2:

t=log2n-1 d0 =1, d[i-1]=2*d[i]+1 т.е. 1, 3, 7, 13, 31, …..


1


Смотрите также файлы