Файл: Решение Разделим систему тел на отдельные тела и запишем уравнения движения каждого тела в отдельности.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1. Через блок массой 2 кг, укреплённый на краю гладкого горизонтального стола, перекинута верёвка, соединяющая грузы 1 и 2 массами 20 кг и 4 кг соответственно. Найти ускорение, с которым движутся гири, и силы натяжения нити по разные стороны от блока. Блок считать однородным диском. Трением гири 2 о наклонную плоскость и трением в блоке пренебречь.
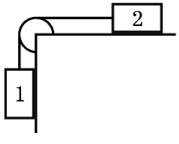
Дано: m = 2 кг; m1 = 20 кг; m2 = 4 кг
a – ? T1 – ? T2 – ?
Решение
Разделим систему тел на отдельные тела и запишем уравнения движения каждого тела в отдельности.
Гиря 1 движется под действием силы тяжести и силы натяжения нити Т1.
Согласно второму закону Ньютона:
(1)Блок вращается под действием сил натяжения нитей Т1 и Т2.
Согласно основному уравнению динамики вращательного движения:
где 
момент инерции блока относительно оси вращения; 
угловая скорость вращения блока; 
момент сил, вращающих блок.Таким образом:
(2)Гиря 2 движется под действием силы натяжения нити Т2. Согласно второму закону Ньютона:
(3)Совместно решая уравнения (1) – (3), находим:
Ответ: а = 7,85 м/с2; T1 = 39,24 Н; T2 = 31,39 Н.2. Платформа в виде однородного диска радиусом 2 м вращается по инерции с частотой 6 оборотов в минуту. Масса платформы 200 кг. В центре платформы стоит человек, масса которого равна 80 кг. С какой частотой будет вращаться платформа, если человек переместится к краю платформы на 50 см? Человека считать точечной массой.
Дано: m = 200 кг; R = 2 м; n0 = 0,1 с-1; m1 = 80 кг; r = 0,5 м
n – ?
Решение
Согласно закону сохранения момента импульса:
где ω = 2πn – угловая скорость вращения,
момент инерции платформы. Тогда: 
Ответ: n = 0,098 об/с.
3. Плоский однородный диск радиусом 1,5 м прикреплён к горизонтальной оси, проходящей через обод диска (его край) перпендикулярно его плоскости. Диск отклонили на угол 60° от положения равновесия и отпустили. Определить линейную скорость нижней точки диска в момент прохождения через положение равновесия.
Дано: R = 1,5 м; φ = 60°
v – ?
Решение
Согласно закону сохранения энергии:
Максимальное значение потенциальной энергии имеем в начальной точке:
Максимальное значение кинетической энергии имеем в положении равновесия:
Имеем: 
откуда 
Ответ: v = 6,26 м/с.
4. Тонкий прямой длинный стержень (неограниченный с одной стороны) несёт заряд, равномерно распределённый по его длине. Напряжённость поля в точке, лежащей на продолжении оси стержня на расстоянии 1 м от его конца, равна 36 В/м. Определить линейную плотность заряда стержня.
Дано: r = 1 м; Е = 36 В/м
τ – ?
Решение
Разобьем стержень на бесконечно малые элементы длиной dx. Заряд такого
элемента будет равен:
а напряженность поля, создаваемого этим элементом в заданной точке: 
Суммарная напряженность от всех элементов стержня:
откуда 
Ответ: τ = 4 нКл/м.
5. Электрическое поле образовано бесконечно длинной нитью с линейной плотностью заряда 10–10 Кл/м. Какую работу совершает поле при переносе точечного заряда 3,2·10–10 Кл из точки, расположенной в 1 см от нити, в точку, расположенную на расстоянии 9 см от нити.
Дано: τ = 10-10 Кл/м; q = 3,2·10–10 Кл; r1 = 0,01 м; r2 = 0,09 м
A – ?
Решение
Определим сначала напряженность поля нити.
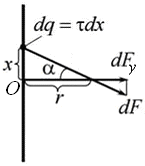
Поскольку нить не является точечным зарядом, напрямую применять закон Кулона нельзя. Разобьем нить на бесконечно малые элементы длиной dx. Заряд каждого такого элемента пропорционален его длине: dq = τdx. Тогда, сила взаимодействия каждого такого элементарного заряда с точечным зарядом, согласно закону Кулона:
Раскладывая эту силу на горизонтальную и вертикальную составляющие, видим, что вертикальные составляющие от симметричных элементов компенсируются. Тогда:
Поскольку 
то 
Т.к.
то 
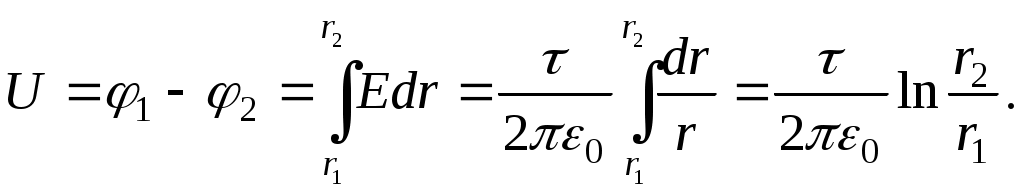
Работа по перемещению точечного заряда в электрическом поле:
Ответ: А = 1,26 нДж.6. Расстояние между пластинами плоского конденсатора 2 см, разность потенциалов 5 кВ. Заряд каждой пластины 20 нКл. Определить энергию W поля конденсатора и силу F взаимного притяжения пластин.
Дано: d = 0,02 м; U = 5∙103 В; q = 2∙10-8 Кл
W – ? F – ?
Решение
Энергия электрического поля конденсатора:
Сила притяжения между пластинами конденсатора:
Учитывая, что электроемкость плоского конденсатора 
где x – расстояние между пластинами, получаем: 
Тогда:
Ответ: W = 50 мкДж; F = 2,5 мН.
7. Электрон, находящийся в однородном электрическом поле, получает ускорение, равное 1014 см/с2. Найти напряжённость электрического поля, скорость, которую получит электрон за 10–6 с своего движения, если начальная его скорость равна нулю, работу сил электрического поля за это время, разность потенциалов, пройденную при этом электроном.
Дано: а = 1012 м/с2; t = 10–6 с
E – ? v – ? A – ? U – ?
Решение
Согласно второму закону Ньютона:
где m = 9,11∙10-31 кг – масса электрона; 
сила, действующая на электрон со стороны поля; е = 1,6∙10-19 Кл – заряд электрона. Тогда:
Скорость, которую получит электрон:
Работа сил электрического поля равна разности кинетических энергий электрона:
С другой стороны: 
откуда 
Ответ: E = 5,69 В/м; v = 1 Мм/с; A = 0,456 аДж; U = 2,85 В.
8. Найти показания амперметра и вольтметра в схеме, изображённой на рисунке. ЭДС батареи ε = 12 В, сопротивления R1 = 400 Ом и R2 = 800 Ом, сопротивление вольтметра RV = 1 кОм. Сопротивлением батареи пренебречь.
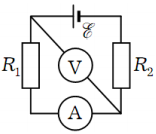
Дано:
ε = 12 В; R1 = 400 Ом; R2 = 800 Ом; RV = 1000 Ом
IA – ? UV – ?
Решение
Полное сопротивление цепи:
Ток через резистор R2:
Показание вольтметра:
Показания амперметра:
Ответ: IA = 7,9 мА; UV = 3,16 В.
9. Сила тока в проводнике равномерно увеличивается от 0 до некоторого максимального значения в течение времени t = 10 с. За это время в проводнике выделилось количество теплоты Q = 1 кДж. Определить скорость нарастания тока в проводнике, если его сопротивление R равно 3 Ом.
Дано: R = 3 Ом; t = 10 с; Q = 103 Дж
k – ?
Решение
Согласно закону Джоуля-Ленца:
Поскольку ток возрастает равномерно, закон его возрастания линейный, т.е. 
Имеем:
Тогда: 
откуда
Ответ: k = 1 А/c.
10. По двум длинным параллельным проводам, расстояние между которыми равно 30 см, текут одинаковые токи в противоположных направлениях. Найти данную силу тока, если индукция суммарного поля токов в точке, удалённой от одного провода на 40 см и от другого на 50 см равна 3 мкТл.
Дано: d = 0,3 м; B = 3∙10-6 Тл; r1 = 0,4 м; r2 = 0,5 м
I – ?
Решение
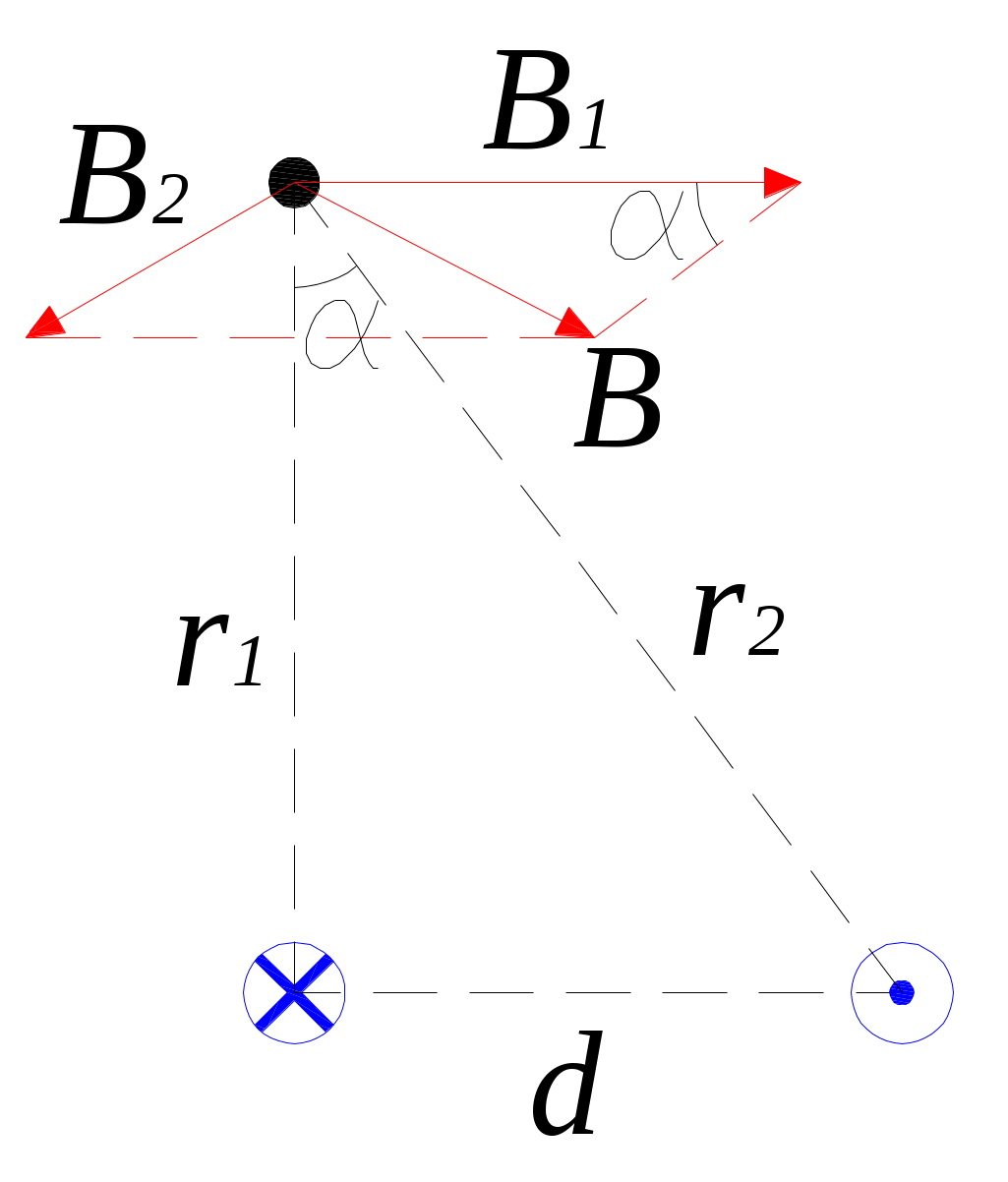
Для нахождения индукции магнитного поля воспользуемся законом Био – Савара – Лапласа. Прямой проводник бесконечной длины создает индукцию:
