Файл: Лабораторная работа Изучение режимов течения жидкости 2ч. Лабораторная работа Изучение гидравлических потерь потока 2ч.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 138
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Часть1 Гидравлика
1. Лабораторная работа № 1. Изучение режимов течения жидкости – 2ч.
2. Лабораторная работа № 2. Изучение гидравлических потерь потока– 2ч.
3. Лабораторная работа № 3. Практическое применение законов гидродинамики – 4ч.
Часть2 Гидравлические машины и гидроприводы
4. Лабораторная работа № 4. Изучение конструкций и характеристик поршневых гидромашин– 2ч.
5. Лабораторная работа № 5. Изучение конструкций и характеристик пластинчатых и шестеренных гидромашин– 2ч.
6. Лабораторная работа № 6. Изучение функций и конструкций управляющей аппаратуры гидравлических приводов– 2ч.
7. Лабораторная работа № 7. Изучение принципов расчета гидравлических схем– 3ч.
Лабораторная работа № 1
ИЗУЧЕНИЕ РЕЖИМОВ ТЕЧЕНИЯ ЖИДКОСТИ
1 Цель работы:
Экспериментальное определение числа Рейнольдса для различных режимов течения жидкости в трубопроводе круглого сечения.
2. Структуры потоков при различных режимах
При ламинарном течении сопротивление движению вызывается вязким трением между слоями, текущими с разными скоростями, закон изменения которых по сечению имеет параболический характер. В слое, непосредственно прилегающим к стенке канала, скорость жидкости равна нулю – происходит так называемое «прилипание» жидкости к стенке. Свойство «прилипания» является одним из характерных особенностей реальной жидкости в отличие от жидкости идеальной. По мере удаления от стенки скорость жидкости увеличивается и достигает максимума в центре канала. Профиль скоростей при ламинарном режиме представляет собой параболу (рисунок 1 а)
Рисунок 1 – Эпюры скоростей при ламинарном (а) и турбулентном (б) режимах движения жидкости в трубе.
При турбулентном режиме движения происходит взаимопроникновение и интенсивное перемешивание содержимого струек жидкости. В результате скорости течения жидкости по сечению выравниваются. Резкое уменьшение скорости по радиусу от центра к периферии трубы происходит лишь в сравнительно узкой области возле стенок. На самой стенке скорость равна нулю, а очень тонкая область (порядка долей миллиметра) приторможенного потока у стенки, движется ламинарно. Называют эту область вязким подслоем. Эпюра скоростей турбулентного потока представлена на рисунке 1, б.
Форма движения жидкости определяется числом Рейнольдса
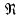, подсчитываемого по формуле
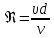, (2)где υ – средняя скорость потока,
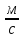;ν – коэффициент кинематической вязкости жидкости,
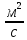;d – диаметр трубопровода, м.
При числах Рейнольдса
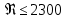движение будет ламинарным. Если 
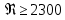, то движение турбулентное. От формы движения жидкости зависит коэффициент, определяющий величину потери напора от трения.В инженерной практике часто требуется знать величину потерь энергии при движении жидкости в трубопроводах. Потери энергии зависят от режима движения жидкости. Следовательно, для того, чтобы определить потери энергии на преодоление сопротивления по длине трубопровода или в местных участках необходимо прежде всего установить режим движения. Возможны два установившихся режима течения жидкостей и газов в трубах:
- ламинарный;
- турбулентный.
Между двумя установившимися режимами движения существует третий, получивший название переходного или неустойчивого режима, в котором могут иметь место и ламинарный и турбулентный режимы в зависимости от величины скорости движения жидкости.
Ламинарное течение – это слоистое течение без перемешивания частиц жидкости и без пульсации скорости. При таком течении все линии тока определяются формой русла, по которому течет жидкость. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, отсутствуют поперечные перемещения жидкости. Таким образом, ламинарный режим является вполне упорядоченным и при постоянном напоре строго установившимся течением (хотя в общем случае может быть и не установившимся).
Турбулентное течение – это течение, сопровождающееся интенсивным перемещением жидкости, пульсацией скоростей и давлений. Движение отдельных частиц носит хаотичный характер
, траектории подчас имеют вид замысловатых кривых.
Объясняется это тем, что при турбулентном течении, наряду с основными продольными перемещениями частиц жидкости вдоль трубопровода, имеют место поперечное и вращательное движение отдельных объемов. Режим движения жидкости зависит от величины средней скорости течения ср,от характерного линейного размера (для круглой трубы этим размером является диаметр d) и от коэффициента кинематической вязкости , определяемого температурой жидкости tC.
Смена режима течения жидкости в трубопроводе происходит при определенной скорости течения кр, которую называют критической. Как показали многочисленные эксперименты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости и обратно пропорционально диаметру dтрубы
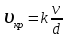. (2.1)Входящий в формулу коэффициент пропорциональности k имеет универсальное значение и одинаков для любых диаметров труб. Это значит, что смена течения происходит при вполне определенном соотношении между скоростью, диаметром и вязкостью , равном:
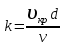. (2.2)Критических скоростей две:
1) верхняя критическая скорость кр.в, когда режим ламинарный сменяется турбулентным;
2) нижняя критическая скорость кр.н, когда турбулентный режим переходит в ламинарный.
Если скорость изменяется в сторону увеличения, то в переходной области преобладает турбулентный режим, если в сторону уменьшения – ламинарный. Оба режима в переходной области неустойчивы, они нарушаются под действием самых незначительных причин. Особенно неустойчивым является ламинарный режим. Поэтому в практике принимают для переходной области режим турбулентный, а за критическую скорость – нижнее ее значение.
Английский физик О. Рейнольдс своими опытами в 1883 г. доказал теоретическое предположение Д.И. Менделеева о существовании ламинарного и турбулентного режимов и установил их зависимость от соотношения определенных физических величин. Указанное отношение было названо числом Рейнольдса, которое для круглых трубопроводов определяется по формуле:
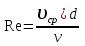
. (2.3)
Переход от одного режима движения к другому происходит при критическом числе Рейнольдса, зависящем от формы сечения канала и определяющемся по формуле:
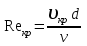, (2.4)Критическое число Рейнольдса для труб круглого сечения приблизительно равно:
Reкр=2320.
Таким образом, получен критерий, позволяющий судить о режиме течения жидкости в трубопроводе. При значениях Re
Многочисленными наблюдениями за движением жидкости в круглой трубе установлено, что если число Рейнольдса меньше значения Re =2320, то режим будет устойчивым ламинарным, а если число больше Re = 4000, то режим устойчиво турбулентный. В переходной области за критическое принимается число Рейнольдса, соответствующее нижнему значению критической скорости:
а) при движении жидкости в круглой трубе Reкр=2320;
б) при движении жидкости в трубах кольцевого сечения, рукавов высокого давления и шлангах Reкр=1600 – 1700.
На практике имеют место как ламинарное, так и турбулентное течение, причем первое течение наблюдается тогда, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно имеет место в трубопроводах, по которым движутся бензин, керосин, спирты, кислоты и другие маловязкие жидкости.
Из величин, входящих в формулу (2.3) неизвестными величинами являются ср. и , которое можно определить, измерив расход и температуру жидкости.
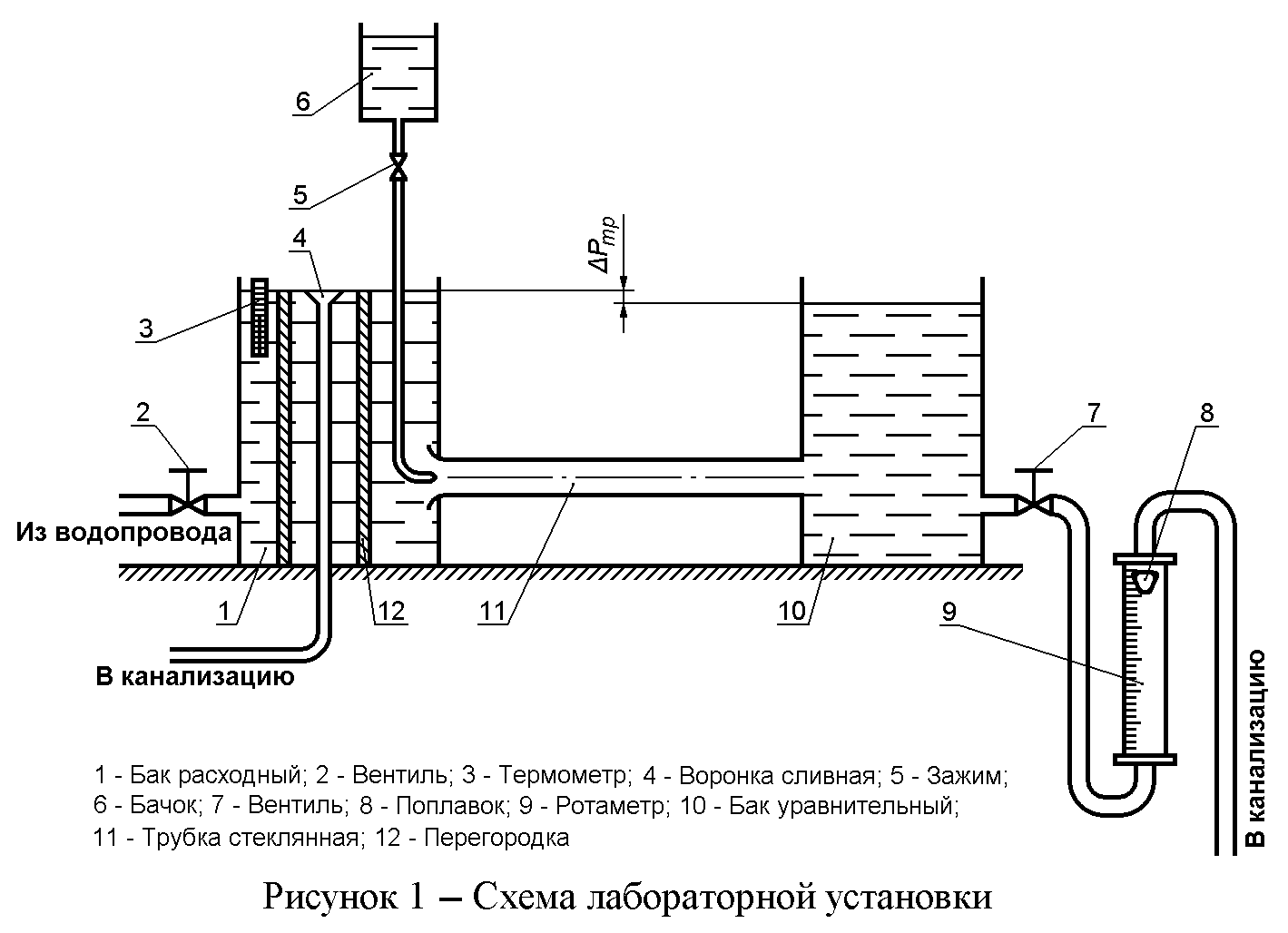
3. Описание лабораторной установки
Лабораторная установка (рисунок 1) состоит из расходного 1 и уравнительного 10 баков, соединённых между собой стеклянной трубкой 11 для визуального наблюдения режимов движения жидкости. Поступающая из водопровода вода через переливную трубу 4 и трубопровод с вентилем 7 сливается в канализацию. Расходный бак разделён перегородками 12 для уменьшения возмущения от потока воды из водопровода. Расход воды, протекающей через стеклянную трубку, регулируется вентилем 7 и определяется положением поплавка 8 ротаметра 9. В крышке расходного бака имеется отверстие для измерения температуры воды термометром 3. Из бачка 6 через тонкий насадок поступает подкрашенная жидкость струйкой, толщина которой регулируется зажимом 5.
4. Порядок выполнения работы
1. Открыть вентиль 2 и заполнить водой из водопровода расходный 1 и уравнительный 10 баки при закрытом вентиле 7. Когда в системе установится определённый уровень воды, а излишки её начнут сливаться в канализацию через переливную трубу 4 вентиль 2 прикрыть, но не полностью, оставляя возможность протока воды через систему.
2. Открыть вентиль 7 так, чтобы верхняя кромка поплавка 8 в ротаметре 9 находилась в районе делений от 8 до 10.
3. Приоткрыть зажим 5 так, чтобы в стеклянной трубке появилась подкрашенная струйка в виде чёткой не размытой линии. Её интенсивность регулируется зажимом 5.
4. Снять показания ротаметра 9 и термометра 3 и занести их в протокол.
5. Открытием вентиля 7 увеличить расход воды через стеклянную трубку 11 до появления на подкрашенной струйке поперечных возмущений небольшой интенсивности. Занести показания ротаметра и термометра в протокол.
6. Открытием вентиля 7 увеличить расход воды через стеклянную трубку 11 до разрушения подкрашенной струйки на отдельные фрагменты, ясно различимые в потоке. Занести показания ротаметра и термометра в протокол.
7. Открытием вентиля 7 увеличить расход воды через стеклянную трубку 11 до полного исчезновения фрагментов подкрашенной струйки и окрашивания воды в конце стеклянной трубки. Занести показания ротаметра и термометра в протокол.
8. Закрыть зажим 5 до полного прекращения поступления подкрашенной жидкости в стеклянную трубку 11. После этого закрыть вентили 2 и 7.
5. Обработка опытных данных
1. Определить расход воды через стеклянную трубку по показателям ротаметра
, используя формулу 
, 
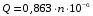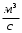.Коэффициент
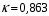получен в результате тарировки ротаметра.2. Определить среднюю скорость потока в стеклянной трубке по формуле
, 
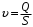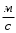,где
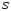– площадь сечения трубки с внутренним диаметром 
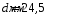.3. Определить кинематический
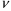и динамический 
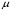коэффициенты вязкости, используя интерполяционную формулу
, 
;
, 
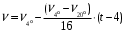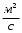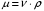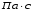.Плотность воды принять равной
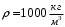, коэффициент кинематической вязкости воды при температуре 
, 
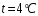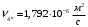; при температуре 
, 
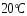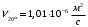.4. Определить число Рейнольдса по формуле
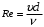.Таблица 1 – Значение кинематического коэффициента вязкости воды в зависимости от температуры tС
| Значение температуры, t, оС | Значение коэф. кинематической вязкости, ∙10-4, м2/с(Ст) | Значение температуры, t, оС | Значение коэф. кинематической вязкости, ∙10-4, м2/с(Ст) |
| +1 | 0.0178 | +11 | 0.0127 |
| +2 | 0.0173 | +12 | 0.0124 |
| +3 | 0.0162 | +13 | 0.0121 |
| +4 | 0.0157 | +14 | 0.0117 |
| +5 | 0.0152 | +15 | 0.0114 |
| +6 | 0.0147 | +16 | 0.0111 |
| +7 | 0.0143 | +17 | 0.0108 |
| +8 | 0.0139 | +18 | 0.0106 |
| +9 | 0.0131 | +19 | 0.0103 |
| +10 | 0.0131 | +20 | 0.0101 |
Результат занести в таблицу 2.
Таблица 1 – Результаты опытов и расчетов
| Опыт | Расход | Температура t, oC | Вязкость 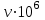 ,  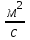| Форма струйки | Рейнольдс Re | Режим | |
| n |  ,  | ||||||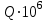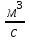
| | |  | | | |  | |
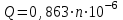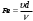| 1 | | | | |  | | ламин. |
| 2 | | | | |  | | ламин. |
| 3 | | | | |  | | перех. |
| 4 | | | | |  | | турб. |
Дать пример расчета для одной из точек.
5. Анализируя полученные значения чисел
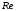при различных формах струйки, сделать вывод о численном значении критического числа Рейнольдса 
при напорном движении жидкости в цилиндрических трубах. 1 2 3 4 5
6. Контрольные вопросы к защите лабораторной работы
1. Назвать физические причины изменения режимов движения жидкости.
2. Описать и обосновать изменение эпюр скорости для ламинарного и турбулентного движения жидкости.
3. Сформулировать смысл числа Рейнольдса с точки зрения теории подобия потоков жидкости.
4. Описать процесс изменения структуры потока при изменении его средней скорости; изменении коэффициента кинематической вязкости; изменении эквивалентного диаметра канала, по которому течет жидкость?
Задача 1.2. Определить диаметр магистрального трубопровода и потери напора в нем для потока с расходом Q . Критическое число Рейнольдса 1900, предельное число Рейнольдса определить по формуле
. Вязкость ν=1сСт. Лабораторная работа №2
Изучение гидравлических потерь потока
№2.1 Изучение местных гидравлических потерь
1.Цель работы
Уяснить физическую сущность гидравлических потерь и методы их определения для различных участков потока и при различных режимах его течения. Определить опытным путем коэффициенты местных сопротивлений, сравнить их с расчетными значениями.
2. Основные теоретические сведения
Местные сопротивления представляет собой короткие участки каналов, характеризуемые резким изменением размеров или конфигурации русла, на которых происходит изменение скорости потока по величине или по направлению.
К местным сопротивлениям относятся: внезапное расширение русла, плавное расширение русла (диффузор), внезапное сужение русла, плавное сужение русла (конфузор), повороты, различная арматура (клапаны, краны, задвижки, фильтры, диафрагмы). Потери энергии на местных сопротивлениях выражают величиной потерь напора и определяют по формуле Вейсбаха
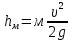, (1)где hм - потери напора на местном сопротивлении;