Файл: 180 тестов Функция одной переменной (30 тестов) Предел функции одной переменной (35 тестов) Производная (45 тестов) Функция двух переменных (40 тестов) Функция (30 тестов).doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 50

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


+1). 2). 3). 4).

УС 4

Время 3
3.2.1.7/1

Производная функции, заданной неявно , равна

1). 2). +3). 4).

УС 3

Время 2
3.2.1.7/2

Производная функции, заданной неявно , равна

1). 2). 3). +4).

УС 4

Время 3

3.2.1.7/3

Производная функции , равна

1). +2). 2 3). 4).

УС 4

Время 3

3.2.1.7/4

Производная функции , равна

1). 2). 3).

+4).

УС 4

Время 3
3.2.1.8/1 Теорема Лагранжа для непрерывной на интервале
и дифференцируемой на функции утверждает, что существует точка ,такая, что:

1. 2. +3.

4.

УС 3

Время 1
3.2.1.8/2 Функции, удовлетворяющие условиям теоремы Лагранжа:

+1. 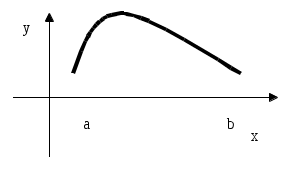2 .
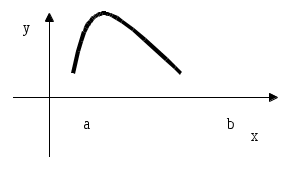3. +4.

УС 4

Время 1
3.2.1.10/1 Функции, удовлетворяющие условиям теоремы Ролля:

+1. 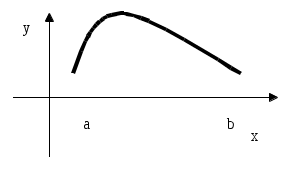2 .
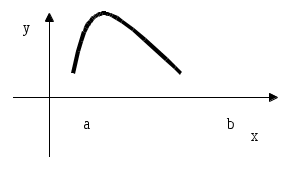3. 4.

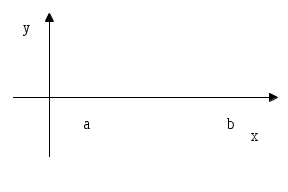
УС 4

Время 1
3.2.1.11/1

Производная второго порядка от функции равна

1). + 2). 3). 4).

УС 3

Время 2
3.2.1.11/2

Производная второго порядка от функции равна

1). cos3x 2). 3cos3x 3). 9sin3x +4). -9sin3x

УС 3


Время 1
3.2.1.11/3

Производная второго порядка от функции равна

+1). -9cos3x 2). 3cos3x 3). 9sin3x 4). -9sin3x

УС 3

Время 1

3.2.2.1/1

Необходимые условия достижения функцией экстремума в точке х:

1). +2). 3). 4).

УС 3

Время 1
3.2.2.1/2

Достаточные условия достижения функцией максимума в точке х0:

1). +2).

3). 4).

УС 3

Время 1

3.2.2.1/3

Достаточные условия достижения функцией минимума в точке х0:

1). +2).

3). 4).

УС 3

Время 1
3.2.2.2/1

Функция возрастает на интервале [a,b], если производная этой функции на этом интервале :

1). постоянна 2). 3). +4).

УС 3

Время 1
3.2.2.2/2

Функция убывает на интервале [a,b], если производная этой функции на этом интервале :

1). постоянна 2). +3). 4).

УС 3

Время 1

3.2.2.3/1

Точку перегиба на интервале [-1,1] имеет функция

1). y=x2 +2). y=x3 3). y= 4). y=2x+5 5). y=ex

УС 4

Время 2

3.2.2.3/2

Точку перегиба на интервале [-1,1] имеет функция

1). y=2x2 2) y= +3). y= x3 4). y=3x-4 5). y=lnx

УС 4

Время 2

3.2.2.3/3

Точка перегиба функции

1).отделяет участок возрастания функции от участка убывания

+2). отделяет участок вогнутости функции от участка выпуклости

3). совпадает с точкой экстремума

4). совпадает с нулем функции.

УС 4

Время 1
3.2.2.4/1

Вертикальную асимптоту х=3 имеет функция

+1). 2). 3). 4).

УС 3

Время 1
3.2.2.4/2

Вертикальную асимптоту х=0 имеет функция

1). +2). 3). 4).
УС 3

Время 1

3.2.2.4/3

Наклонная асимптота функции имеет вид:

1). y=2x+3 +2).y=2x 3). y=3x 4). Не существует
УС 3

Время 1
Тесты по высшей математике-3 часть

Функция двух переменных (40 теста)

3.3.1.1/1

Значение функции двух переменных z=2х-y+15 в точке A(-2,1) равно
Ответ10

УС 1

Время 1
3.3.1.1/2

Значение функции двух переменных z=3х-2y+16 в точке A(1,2) равно
Ответ 15

УС 1

Время 1
3.3.1.2/1

Предел функции двух переменных z=х2+2y2+6 при равен

Ответ 8

УС 2

Время 1
3.3.1.2/2

Предел функции двух переменных z=х2-y2+5 при равен

Ответ 5

УС 2

Время 1

Время 1
Время 1

3.3.1.3/1

Непрерывными функциями двух переменных в области являются

1). +2). +3). 4).

УС 3

Время 2
3.3.1.3/2

Непрерывными функциями двух переменных в области являются

+1). +2) . 3). 4).
УС 3

Время 2
3.3.2.1/1

Частная производная функции двух переменных равна

+1). 2).

Смотрите также файлы