Файл: Инженерный вестник Дона.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 28

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Инженерный вестник Дона, №4 (2018) ivdon.ru/ru/magazine/archive/n4y2018/5410




Анализ устойчивости тренда временных рядов параметра технического объекта с использованием показателя Херста

С.И.Клевцов

Южныйфедеральныйуниверситет,Ростов-на-Дону
Аннотация: Прогнозная оценка состояния технического объекта базируется на определение возможных значений контролируемых параметров на прогнозируемом участке времени и осуществляется в процессе функционирования объекта. Вычисления проводятся, как правило, в фоновом режиме и важно оценить минимальную выборку значений параметров, которую можно использовать для прогноза. В статье показана возможность использования показателя Херста для определения персистентности временного ряда параметра объекта и представлена схема оценки минимального объема выборки, который может быть использован для достоверного прогноза изменения параметра с использованием методов прогнозирования временных рядов.

Ключевые слова: временной ряд, показатель Херста, прогноз, оценка, тренд, устойчивость, персистентность, значение, параметр, объект, массив данных.
В процессе своего функционирования техническая система подвергается воздействию внешних и внутренних факторов. Ее параметры при этом изменяются вплоть до недопустимых значений, что может привести к выходу из строя или нештатной ситуации. Эти изменения будут медленными, если связаны с деградацией элементов объекта. Если же объект непрерывно меняет свое состояние, как, например, автомобиль во время движения, то изменения параметров могут происходить достаточно быстро и для предотвращения опасной ситуации необходимо прогнозировать эти изменения. Исходными данными для прогнозирования являются временные ряды контролируемых параметров [1, 2]. Используя методы прогнозирования временных рядов, можно оценить состояние объекта в следующие после текущего моменты времени и, в случае возможности возникновения нештатной ситуации, предпринять необходимые меры [3, 4].

Однако, условием достоверного прогноза является устойчивость тренда временного ряда [5, 6, 7]. Для проведения такой оценки можно использовать метод нормированного размаха, основанный на расчете показателя Херста [8,


9, 10]. Показатель Херста используется для анализа временных рядов в различных отраслях науки, например, в экономике, медицине, инфокоммуникационных технологиях [5, 6, 9, 10].

Показатель Херста Hопределим из соотношения [9, 10, 11]:

R/S = (τ/α)H ,

где α= 0,5 [8, 11]

Алгоритм вычисления Hприведен в работах [8, 9, 11].

Известно, что если H > 0,6, то анализируемый временной ряд является персистентным и обладает трендоустойчивостью и высокой надежностью прогноза. Если H 0,5 ± 0,1, то ряд представляет собой белый шум, характеризуется наименьшей надежностью прогноза. При H  0,3 ± 0,1 ряд является антиперсистентным, обладает выраженными фрактальными свойствами.

Прогнозирование временного ряда контролируемого параметра целесообразно осуществлять в реальном времени. В процессе предпрогнозной подготовки ряда выявляется возможность использования стандартных методов прогнозирования, для чего осуществляется анализ его трендоустойчивости. Однако считается, что для такого анализа с использованием показателя Херста необходима обработка больших массивов данных, порядка нескольких тысяч значений [5, 7]. Это может серьезным образом повлиять на производительность систем контроля объекта, поскольку такой процесс стараются сделать фоновым. Возможность снижения необходимых для анализа трендоустойчивости объемов данных может упростить оценку и реализовать ее на
фоновом уровне работы микроконтроллеров систем мониторинга и управления объектом.

Анализ трендоустойчивости временных рядов быстроменяющихся параметров динамических объектов проводился на примере временного ряда угловой скорости автомобиля. Данные снимались с датчика угловой


скорости, который обычно используется в системах курсовой устойчивости автомобиля. На рис. 1 представлена временная зависимость угловой скорости относительно вертикальной оси (оси Z).



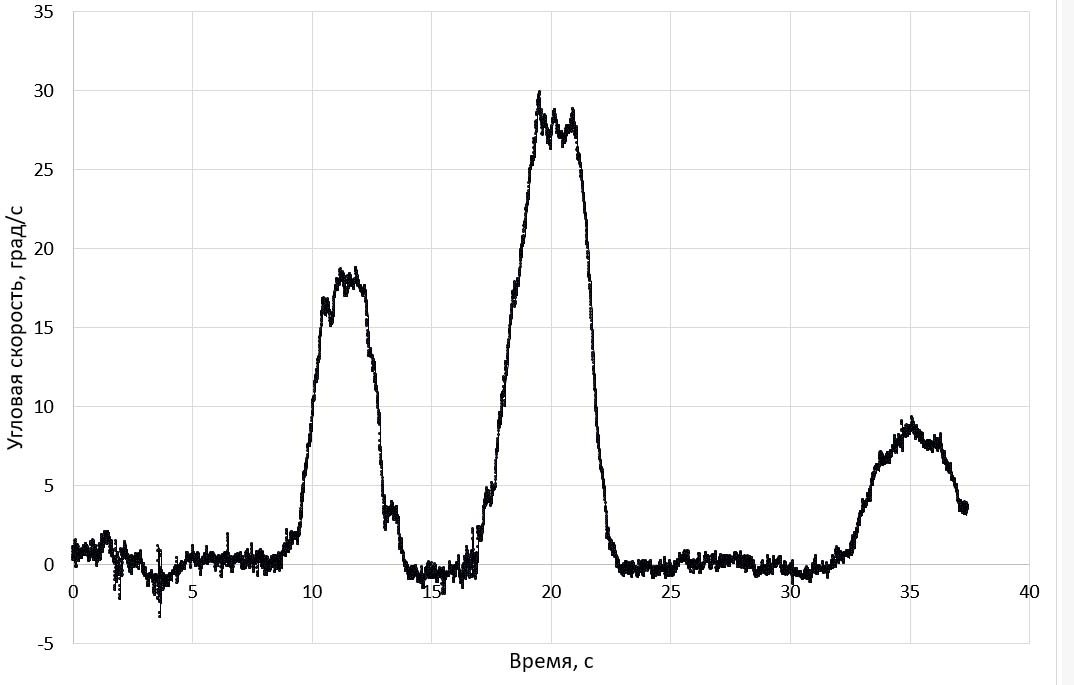
Рис. 1. – График изменения угловой скорости по оси Z

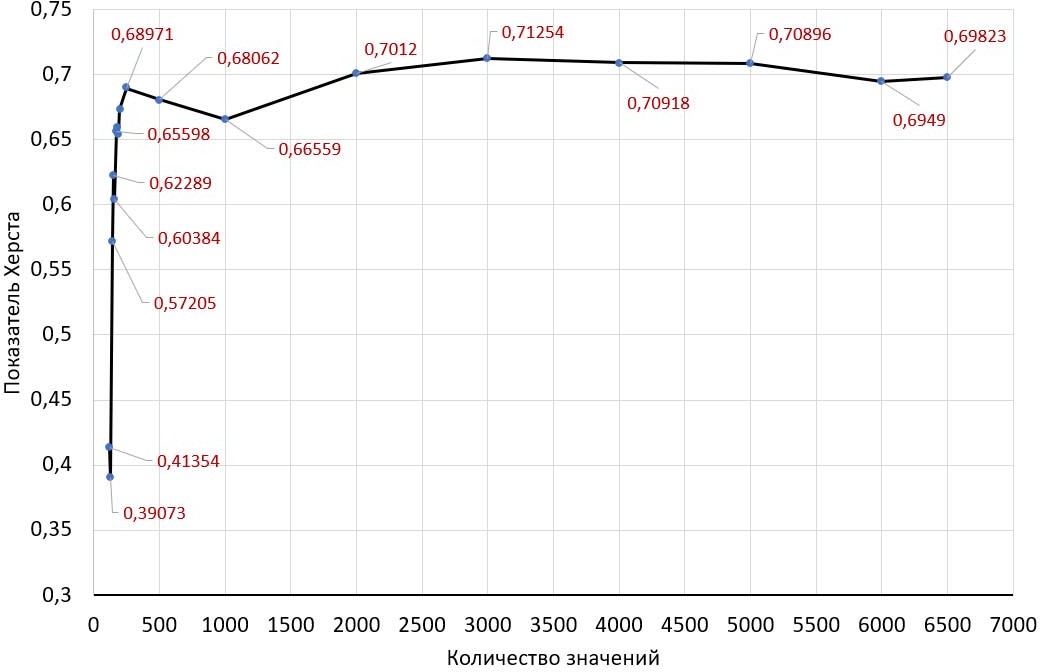Был рассчитан показатель Херста для различных объемов данных, от нескольких тысяч значений до нескольких десятков значений (рис.2).

Рис. 2. – График изменения Нот объема выборки


Анализ данных показывает, что рассматриваемый ряд имеет устойчивый тренд, следовательно, использование стандартных методов прогнозирования временных рядов может дать достоверные результаты.

Однако, представленные результаты показывают, что существует критическое значение объема выборки, при котором анализ трендоустойчивости возможен. Этот вывод подтверждается результатами анализа графика изменения значения Log(R/S) от величины Log(τ/2) (рис.3). На рис. 3 представлены зависимости для оценки изменения показателя Херста для различных объемов выборки значений параметра. Показатель Н равен тангенсу наклона участка графика. Если на каком-либо из участков
графика зафиксировано отрицательное приращение, то начало такого участка служит оценкой критического значения объема выборки. Для данного ряда это 190 ± 10 значений ряда. На рис. 2 приведены усредненные значения показателя Н.



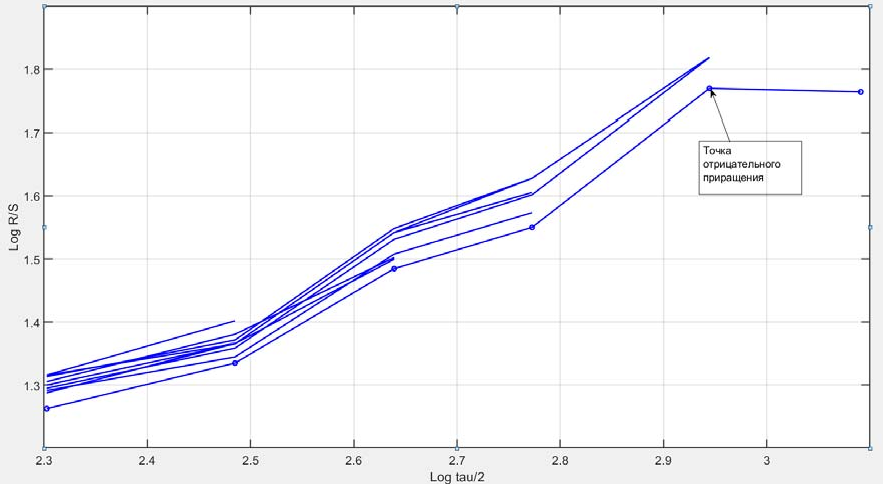
Рис. 3. – Графики для оценки динамики изменения показателя Херста Таким образом, для каждого временного ряда параметра технического

объекта существует минимальный объем выборки значений, при котором анализ ряда дает достоверные результаты о его трендоустойчивости и,


следовательно, возможности прогнозной оценки параметра. Предпрогнозный анализ выборки меньшего размера может привести к неверному выводу о соответствии или несоответствии ряда критерию персистентности, что приведет к недостоверному прогнозу параметра.

Литература


  1. Клевцов С.И. Моделирование алгоритма краткосрочного прогнозирования изменения быстроизменяющейся физической величины в реальном времени // Инженерный вестник Дона. 2012. №3 URL: ivdon.ru/ru/magazine/archive/n3y2012/920

  2. Klevtsov S.I. Identification of the State of Technical Objects Based on Analyzing a Limited Set of Parameters. // 2016 International Siberian Conference on Control and Communications, SIBCON 2016. Proceedings. 2016. pp. 749-752.

  3. Клевцов С.И., Клевцова А.Б., Буринов С.В. Модель параметрической качественной иерархической оценки состояния технической системы // Инженерный вестник Дона, 2015, №3 URL: ivdon.ru/ru/magazine/archive/n3y2015/3088

  4. Lihua Sun , Yingjun Guo, Haichao Ran. A New Method of Early Real- Time Fault Diagnosis for Technical Process// Electrical and Control Engineering (ICECE), 2010 International Conference, 2010. Wuhan. China. pp. 4912 – 4915.

  5. Peters, E. Fractal Market Analysis. Applying Chaos Theory to Investment &Economics. J. Wiley & Sons, New York, 1994. 315p.

  6. James B. Bassingthwaighte, Gary M. Raymond. Evaluation of the Dispersional Analysis Method for Fractal Time Series. // Ann Biomed Eng. 1995. V.23(4). pp. 491–505.

  7. Резниченко А.А., Лучинин А.В., Старченко И.Б. Анализ временных рядов КИГ с использованием метода фрактальной обработки // Инженерный вестник Дона, 2012, №4 (часть 1). URL: ivdon.ru/ru/magazine/archive/n4p1y2012/1133




  1. Калуш Ю. А., Логинов В. М. Показатель Хёрста и его скрытые свойства. // Сибирский журнал индустриальной математики. 2002. Т. 5. №4. С. 29–37

  2. Антипов О.И., Неганов В.А. Применение метода нормированного размаха Хёрста к анализу стохастических временных рядов в импульсных стабилизаторах напряжения. //Физика волновых процессов и радиотехниче- ские системы. 2009. Т.12. №3. С. 78-85

  3. Roel F. Ceballos, Fe F. LargoOn. The Estimation of the Hurst Expo- nent Using Adjusted Rescaled Range Analysis, Detrended Fluctuation Analysis and Variance Time Plot: A Case of Exponential Distribution. // Imperial Journal of Interdisciplinary Research (IJIR). 2017. Vol 3, Issue 8, pp. 424-434

  4. Кратович П.В. Предпрогнозный анализ временных рядов финансовых данных на основе методов фрактального анализа // Молодой ученый. Ежемесячный научный журнал. 2010. № 1–2 (13). Том I. С. 11-18

References


  1. Klevcov S.I. Inženernyj vestnik Dona (Rus), 2012. №3. URL: ivdon.ru/ru/magazine/archive/n3y2012/920

  2. Klevtsov S.I. . 2016 International Siberian Conference on Control and Communications, SIBCON 2016. Proceedings. 2016. pp. 749-752.

  3. Klevcov S.I., Klevcova A.B., Burinov S.V. Inženernyj vestnik Dona (Rus),

№3 (2015). URL: ivdon.ru/ru/magazine/archive/n3y2015/3088

  1. Lihua Sun, Yingjun Guo, Haichao Ran. Electrical and Control Engineering (ICECE), 2010 International Conference, 2010. Wuhan. China. pp. 4912 – 4915.

  2. Peters, E. Fractal Market Analysis. Applying Chaos Theory to Investment &Economics. J. Wiley & Sons, New York, 1994. 315p.

  3. James B. Bassingthwaighte, Gary M. Raymond. Ann Biomed Eng. 1995. V.23(4). pp. 491–505.




  1. Reznichenko A.A., Luchinin A.V., Starchenko I.B. Inzhenernyj vestnik Dona, 2012, №4 (part 1). URL: ivdon.ru/ru/magazine/archive/n4p1y2012/1133

  2. Kalush YU. A., Loginov V. M. Sibirskij zhurnal industrial'noj matematiki. 2002. V. 5. №4. pp. 29–37

  3. Antipov O.I., Neganov V.A. Fizika volnovyh processov i radiotekhniche- skie sistemy. 2009. V.12. №3. pp. 78-85

  4. Roel F. Ceballos, Fe F. LargoOn. Imperial Journal of Interdisciplinary Research (IJIR). 2017. Vol 3, Issue 8, pp. 424-434

  5. Kratovich P.V. Molodoj uchenyj. Ezhemesyachnyj nauchnyj zhurnal. 2010. № 1–2 (13). V. 1 pp. 11-18

Смотрите также файлы