Задание. Для функции ???? = (2???? + 3)???? 5???? : 1. Найти область определения, точки разрыва. 2. Исследовать функцию на четность, периодичность. 3. Исследовать поведение функции на концах области определения. Указать асимптоты. 4. Найти промежутки монотонности. Точки экстремума. 5. Найти промежутки выпуклости. Точки перегиба. 6. Найти площадь фигуры, ограниченной графиком функции ???? = (2???? + 3)???? 5???? и прямыми ???? = 0, ???? = 2, ???? = 0. Результаты исследования оформить в виде таблицы.

Область определения	(-∞;+∞)
Четность, периодичность	Функция не является ни четной, ни нечетной Функция непериодическая.
Поведение на концах области определения
Асимптоты	Вертикальных асимптот нет. у=0 горизонтальная асимптота при х→-∞
Промежутки монотонности	Функция убывает при х(-∞;-1,7), и возрастает при х(-1,7;+∞)
Точки экстремума	Х=-1,7
Промежутки выпуклости	Выпукла при х(-1,9;+∞),вогнута при х(-∞;-1,9)
Точки перегиба	X=-1,9
Площадь криволинейной трапеции

1. 
   D(y) = (-∞;+∞)
   
2. 
   Так как у(-х)≠у(х), у(-х)≠-у(х), то функция не обладает свойствами четности или нечетности. Следовательно, график функции не симметричен ни относительно оси Оу, ни начала координат.
   
3. 
   Области определения
   

---

4. 
   Если y=kx+b –наклонная асимптота, то
   

найдем   
значит, при   наклонных асимптот нет.

 

5. 
   Вычислим производную функции и найдем критические точки
   

y'=2e^5x +5(2x+3) e^5x = e^5x (2+10x+15)= e^5x (10x+17)

Производная существует при любых х(-∞;+∞)

6. 
   Решим уравнение e^5x (10x+17) = 0→10x+17=0→x=-1,7
   

Следовательно, точка х=-1,7 критическая. Найдем знак производной справа и слева от полученной точки.

+

- -1,7 x

З начит, функция убывает при х(-∞;-1,7), и возрастает при х(-1,7;+∞)

Отсюда следует, что х=-1,7 точка минимума, точка максимума

7. 
   Найдем производную второго порядка от рассматриваемой функции
   

y'(x)=5e^5x (10x+17)+10e^5x=e^5x(50x+95)

Вторая производная существует при любых значениях 

х(-∞;+∞)

Найдем точки, где

y''=0 : e^5x (50x+95)=0→50x+95=0→x=-1,9

Н айдем знак второй производной справа и слева от полученной точки.

+

- -1,9 x



X=-1,9 точки перегиба,

8. 
   Значит, функция выпукла при х(-1,9;+∞),вогнута при х(∞;-1,9)И зобразим фигуру:
   

у

5-10⁵

4-10⁵

3-10⁵

2-10⁵

1-10⁵

---

-1 0 1 2 х

Д 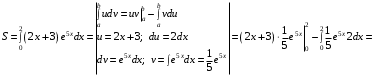ля определения площади фигуры используем формулу   .

 

---

Смотрите также файлы

• Лекции заполните таблицу Факторы риска возникновения сдвг.docx

• Протокол (форма) Фамилия, имя, отчество Алекберова Галина Сергеевна, Алекберов Гаджи Гамизович.docx

• Сценарий последнего звонка.docx

• Тема Философия Возрождения.docx

• Контрольная работа 1 семестр по дисциплине Физика Вариант 2 студент гр. Иб560221 Воробьева Елена Александровна.docx