Файл: Вариант 14 Исследовать числовой ряд на сходимость Так как, то. Ряд сходится, так как ряд с общим членом сходится при и расходится при. В данном случае. Следовательно, сходится и ряд с общим членом по первому признаку сравнения. Ответ.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант № 14
-
Исследовать числовой ряд на сходимость: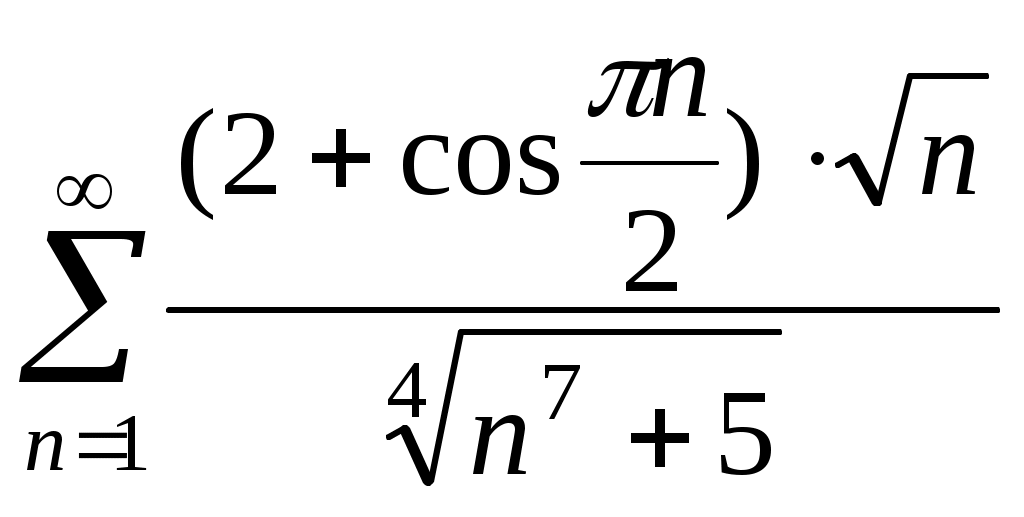 .
.
Так как
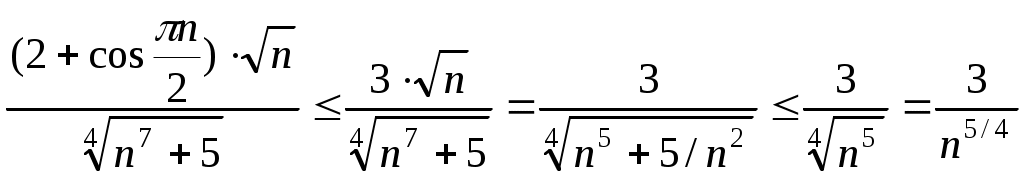 . Ряд
. Ряд 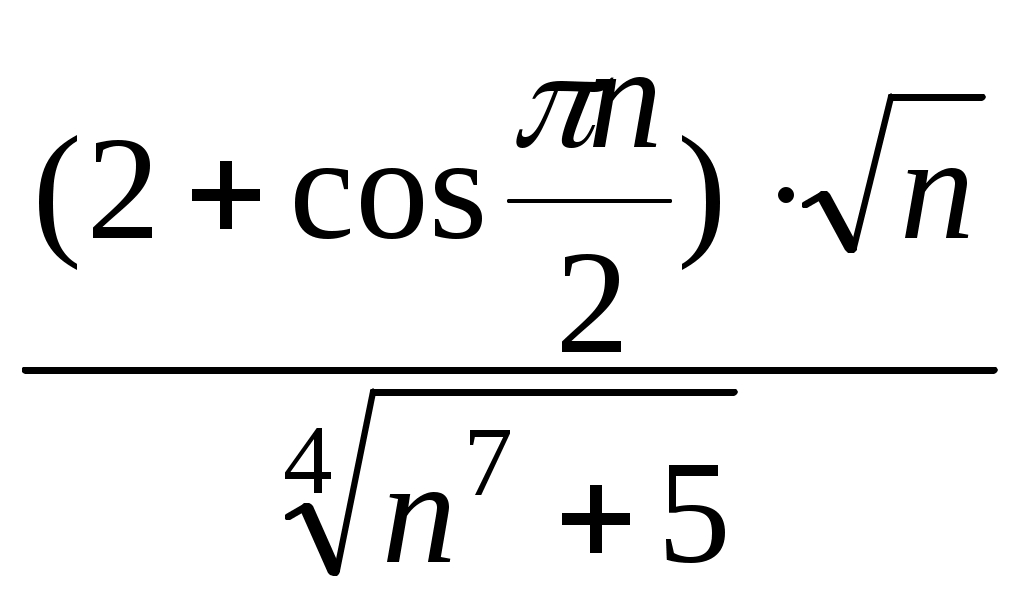 по первому признаку сравнения. Ответ: Ряд сходится.
по первому признаку сравнения. Ответ: Ряд сходится.-
Исследовать числовой ряд на сходимость: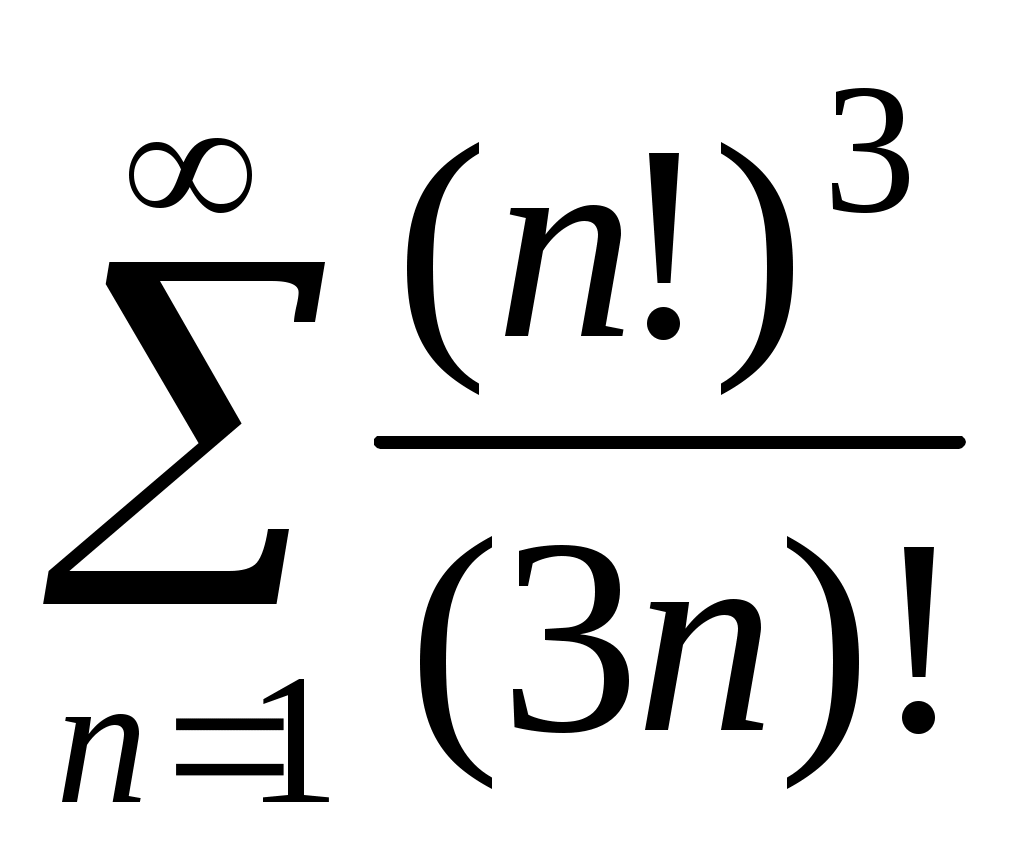 .
.
Применим признак д,Аламбера:
Предел равен отношению коэффициентов при старших степенях, если эти степени одинаковы. Следовательно, данный ряд сходится. Ответ: Ряд сходится.
-
Исследовать числовой ряд на сходимость: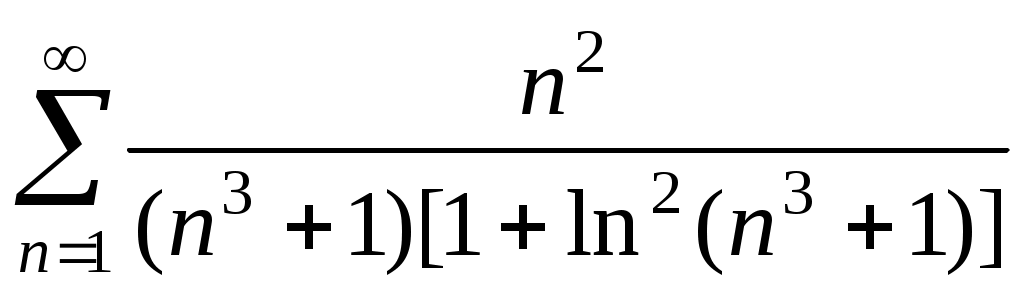 .
.
Имеем
. Интеграл сходится, следовательно, сходится и данный ряд. Ответ: Ряд сходится.
-
Исследовать ряд на абсолютную или условную сходимость: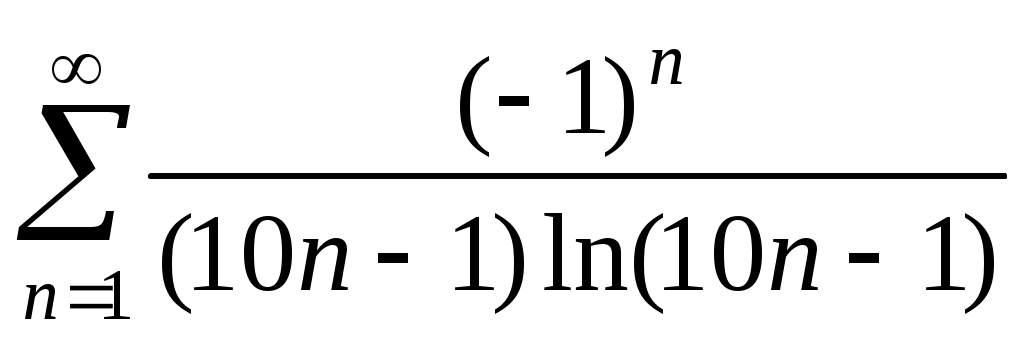 .
.
Исходный ряд является знакочередующимся рядом и удовлетворяет всем условиям теоремы Лейбница. Действительно, по абсолютной величине члены ряда монотонно убывают, а общий член ряда по абсолютной величине стремится к нулю. Рассмотрим ряд
-
Определить область сходимости функционального ряда: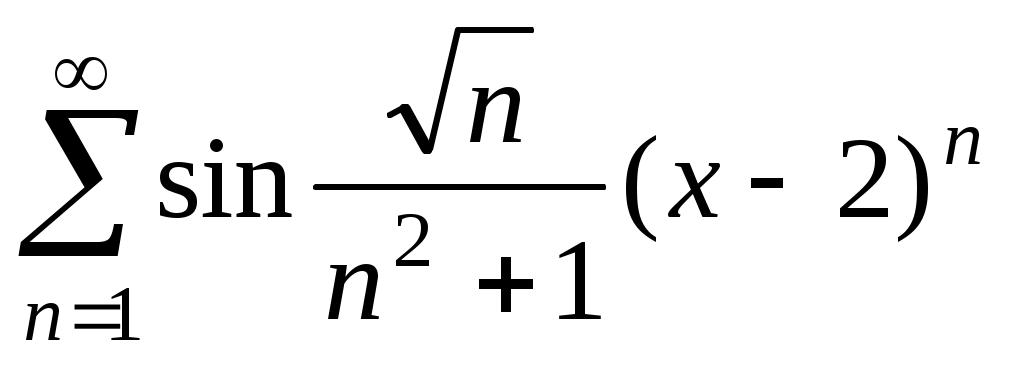 .
.
Для сходимости ряда необходимо, чтобы
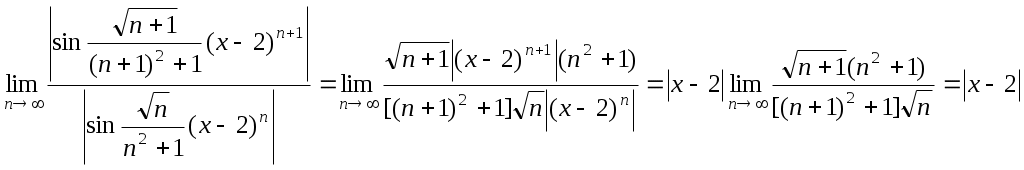 . Ряд сходится, если этот предел будет меньше единицы:
. Ряд сходится, если этот предел будет меньше единицы: -
Определить область сходимости функционального ряда: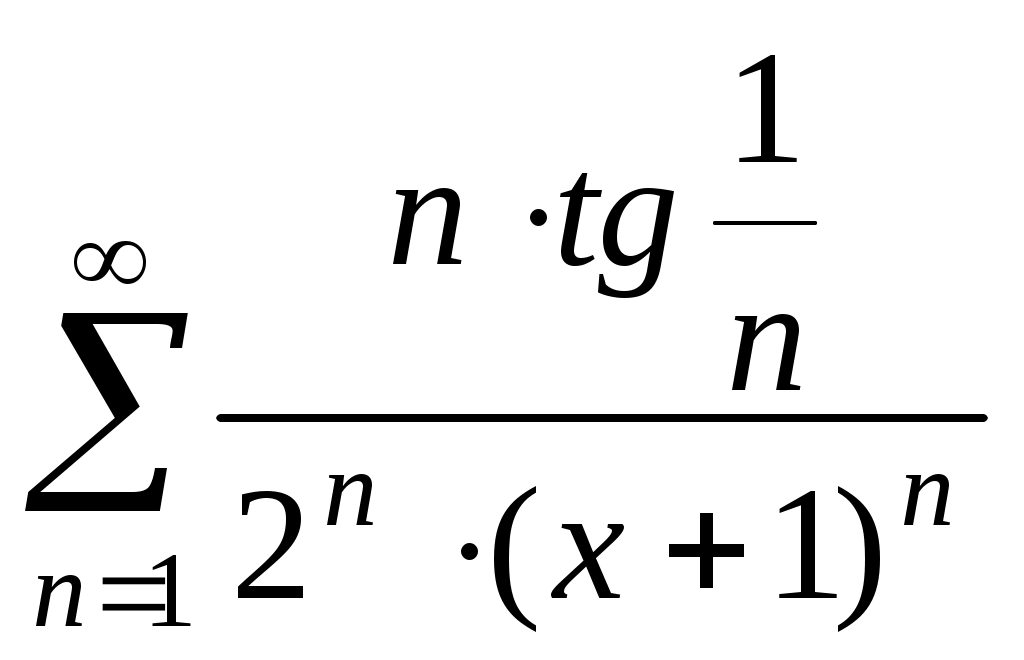 .
.
Применим признак д,Аламбера к ряду
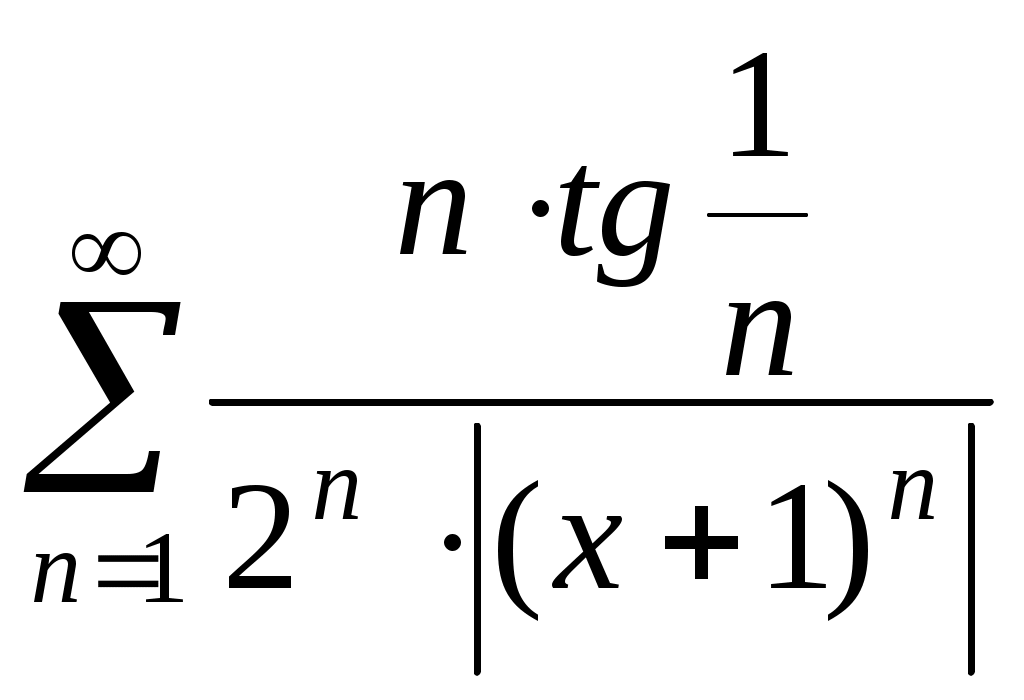 :
: 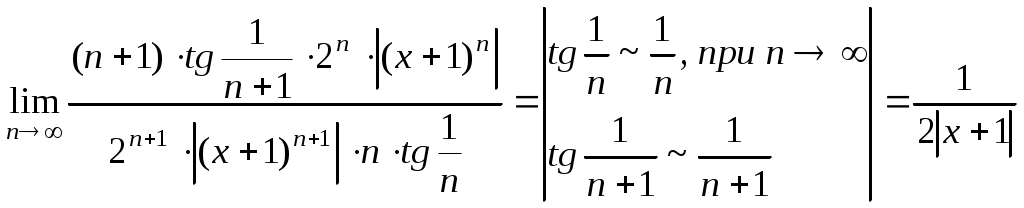 . Ряд сходится, если этот предел будет меньше единицы:
. Ряд сходится, если этот предел будет меньше единицы: . Ответ: Областью сходимости ряда является множество
-
Определить область сходимости функционального ряда: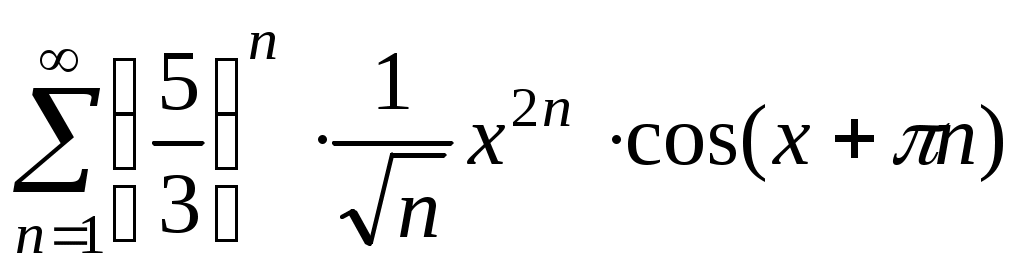 .
.
Поскольку всегда
-
Разложить указанную функцию в ряд Тейлора по степеням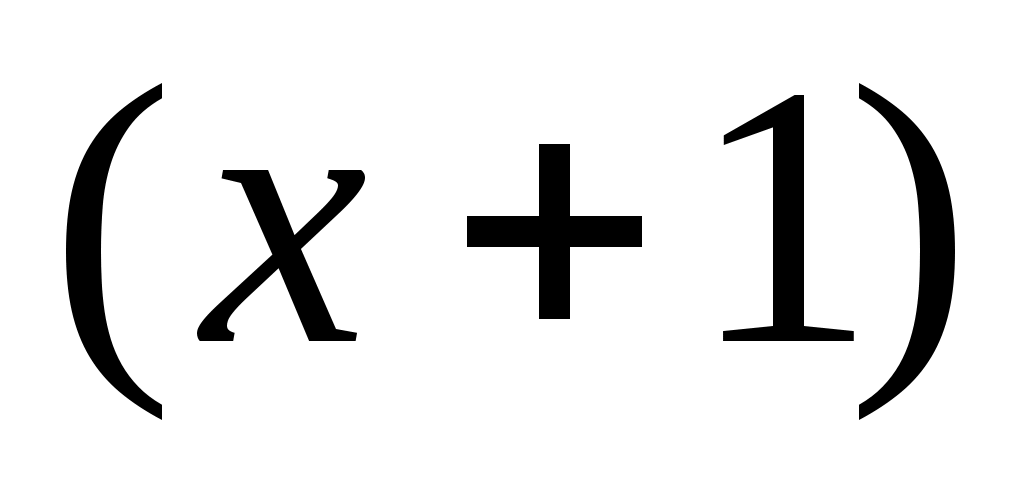 . Указать область сходимости:
. Указать область сходимости: 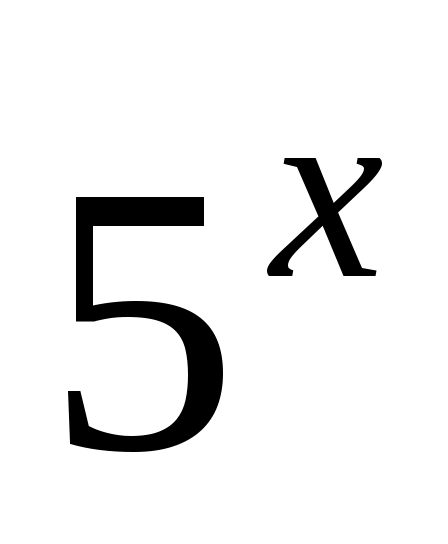 .
.
Воспользуемся известным разложением функции
Или
Ответ:
-
Указанную функцию разложить в ряд Маклорена, используя разложения в ряд функций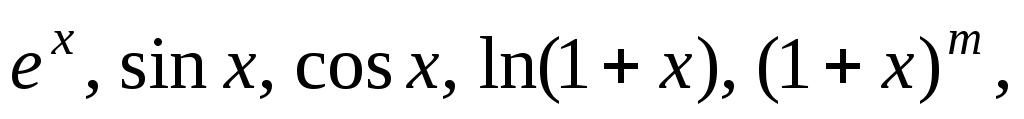 указать область сходимости:
указать область сходимости: 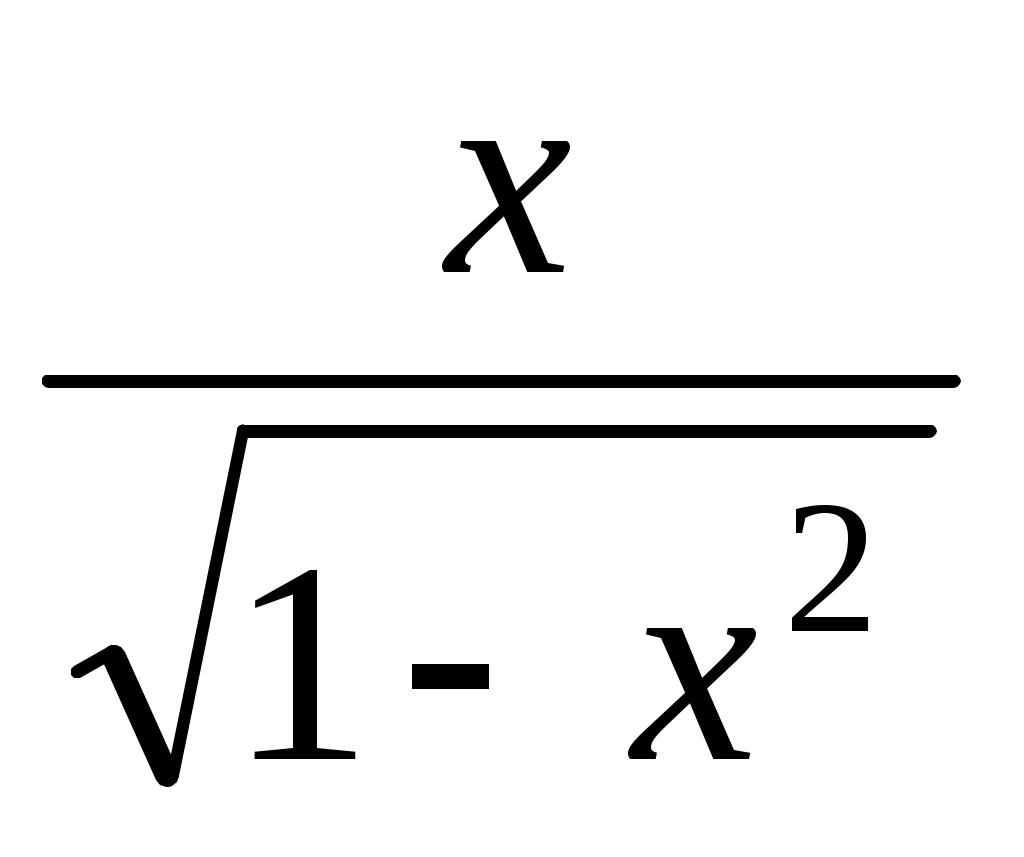 .
.
Преобразуем данную функцию:
-
Вычислить приближённо с точностью до 10-4: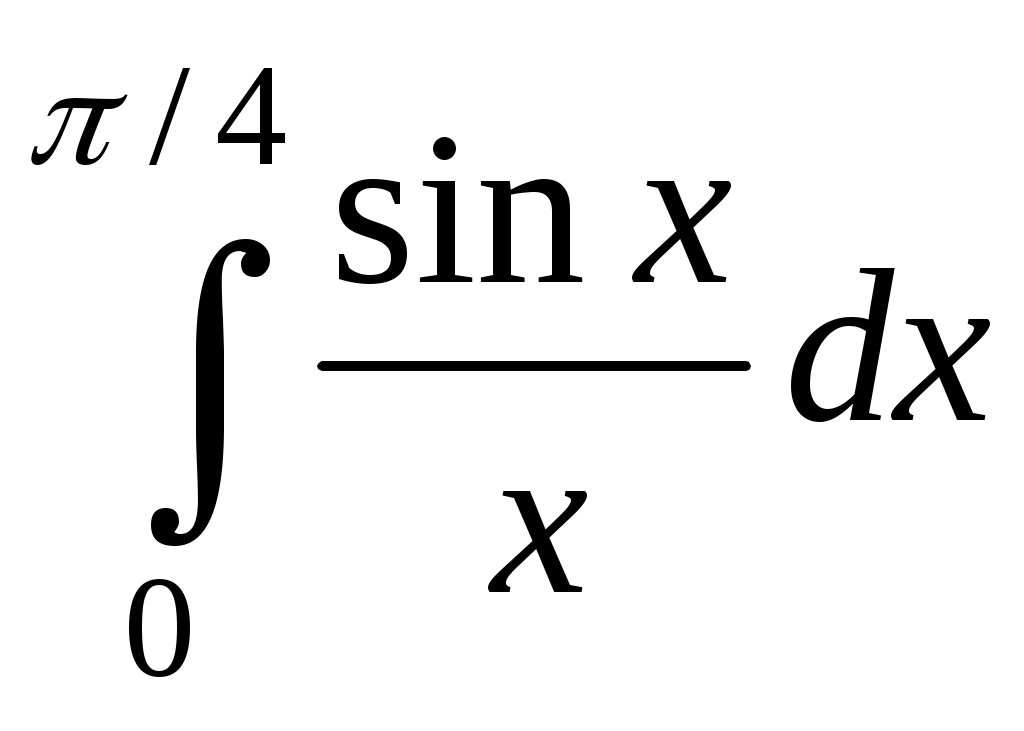 .
.
Воспользуемся формулой