Файл: Вариант 14 Исследовать числовой ряд на сходимость Так как, то. Ряд сходится, так как ряд с общим членом сходится при и расходится при. В данном случае. Следовательно, сходится и ряд с общим членом по первому признаку сравнения. Ответ.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. В данном случае 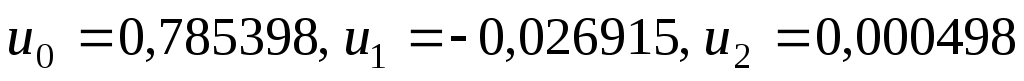 . Очевидно, что
. Очевидно, что 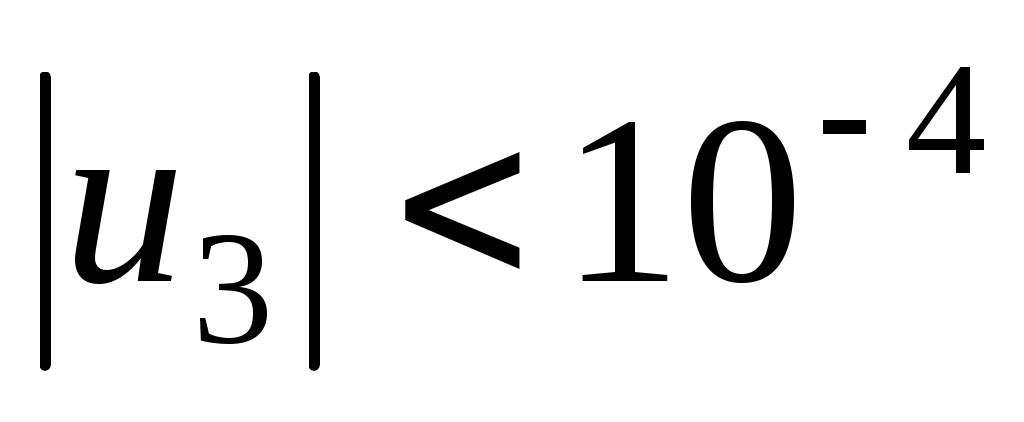 . Следовательно, достаточно взять три первых слагаемых:
. Следовательно, достаточно взять три первых слагаемых: 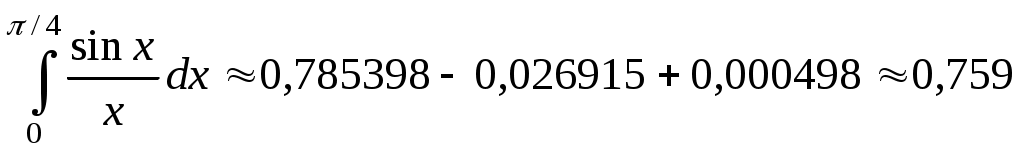 . Ответ:
. Ответ: 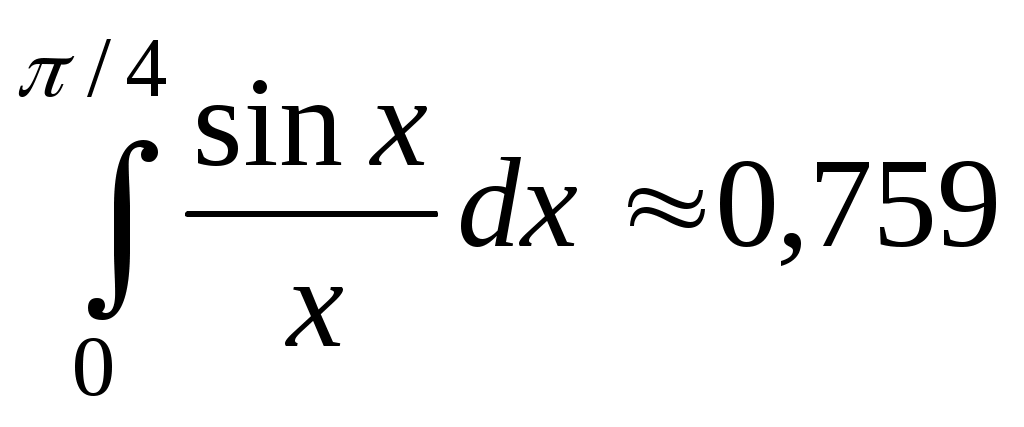
Известно, что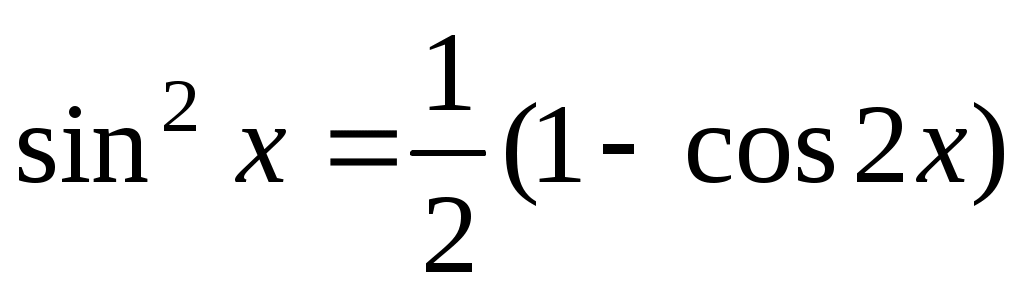 . Так как
. Так как 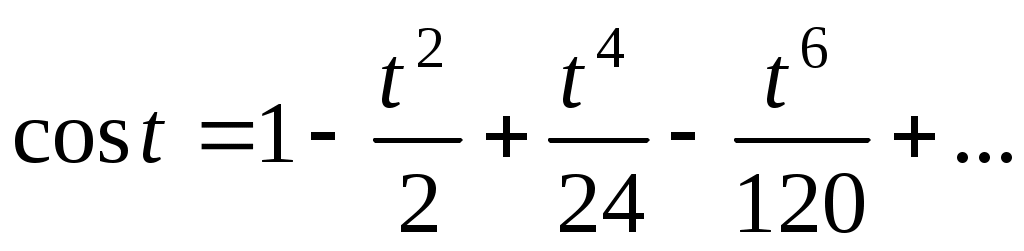 , то
, то 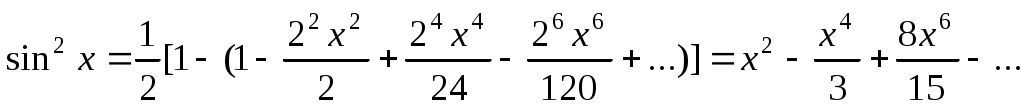 .. Следовательно,
.. Следовательно,
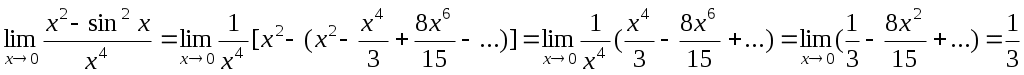 Ответ:
Ответ: 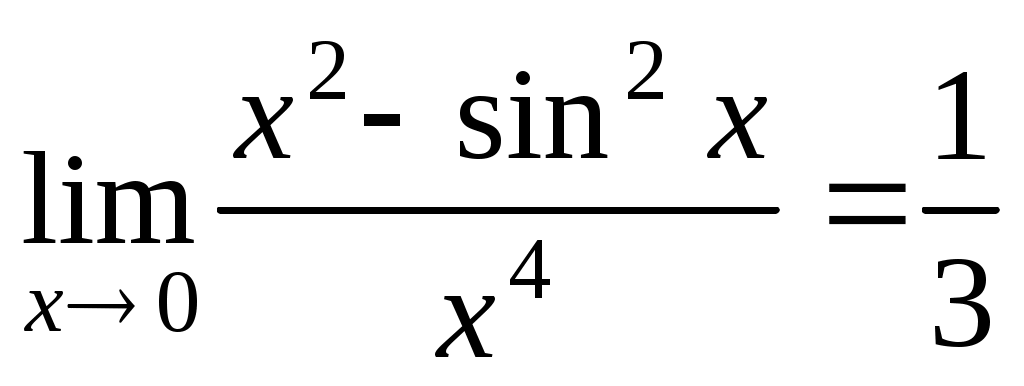 .
.
Преобразуем ряд:
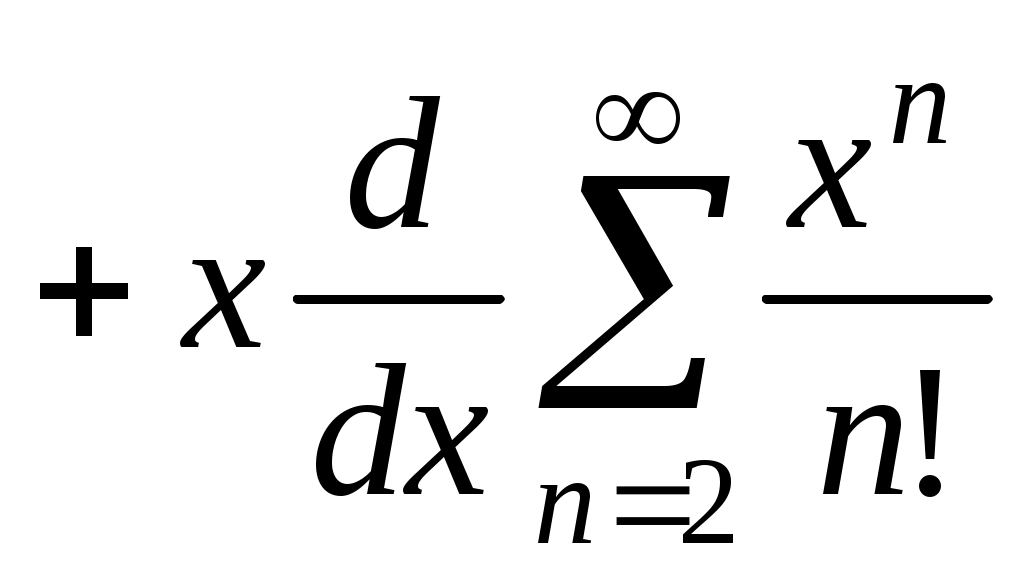 . Но
. Но 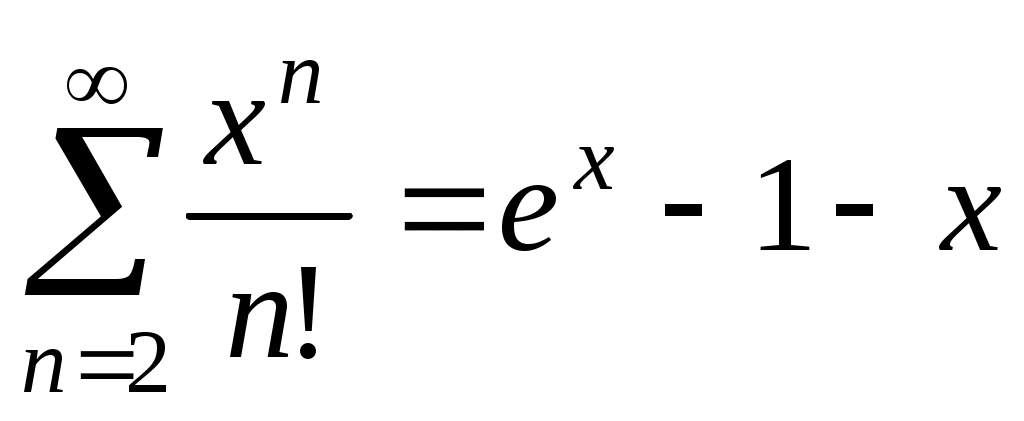 , т.е. это разложение в ряд функции
, т.е. это разложение в ряд функции 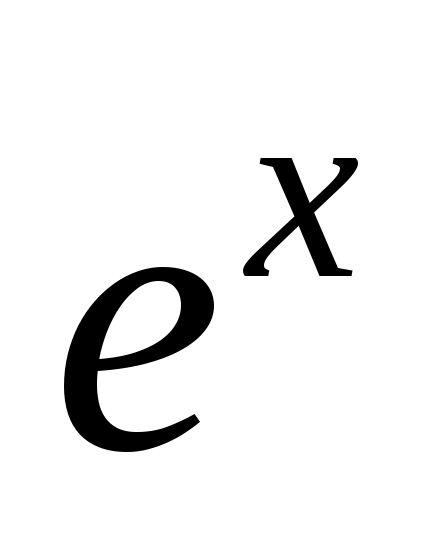 без двух первых членов. Следовательно,
без двух первых членов. Следовательно, 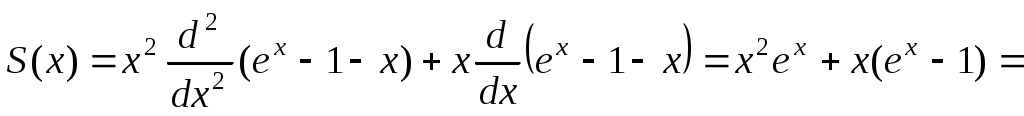
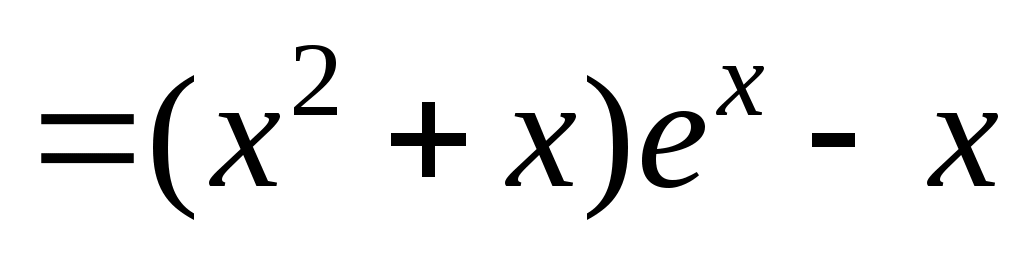 . Ответ:
. Ответ: 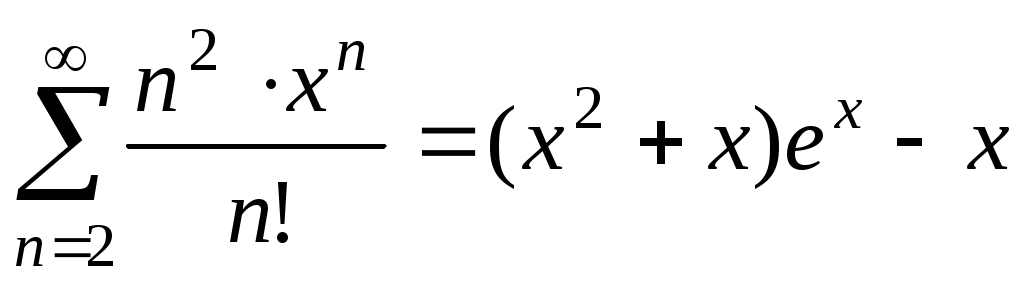 .
.
Обозначим сумму ряда через S(x). Тогда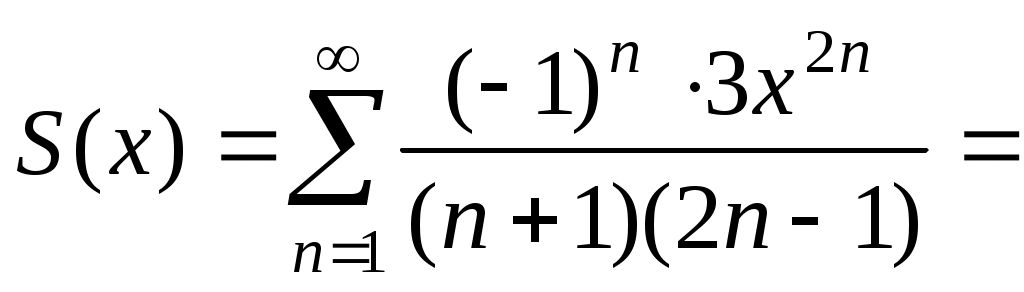
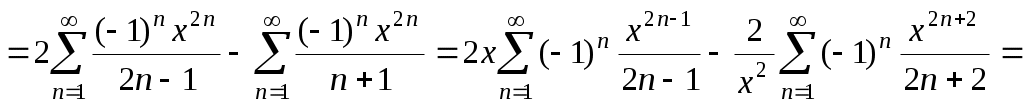
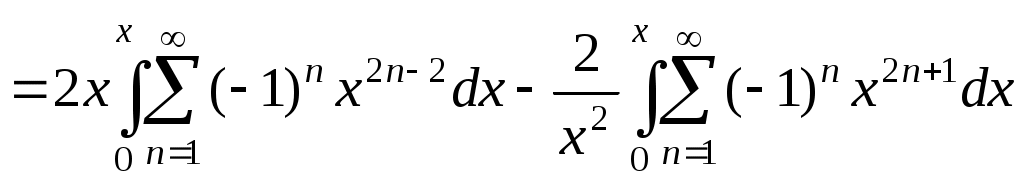 . Но
. Но 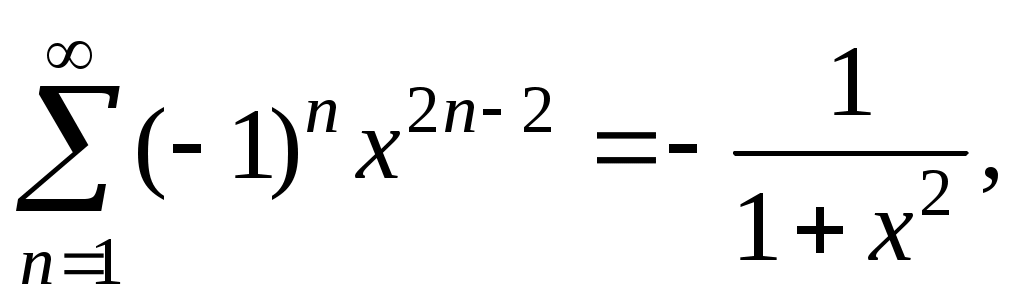
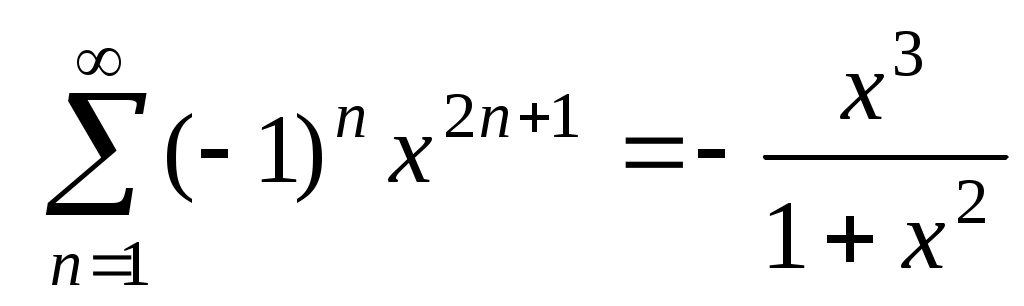
есть суммы бесконечно убывающих геометрических прогрессий при . Следовательно,
. Следовательно, 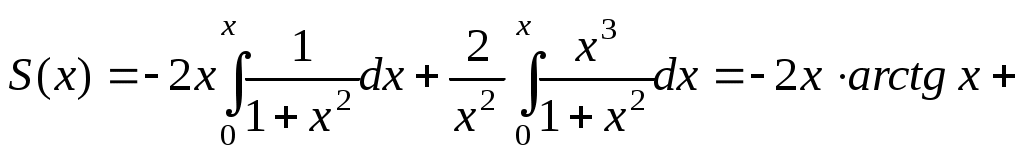
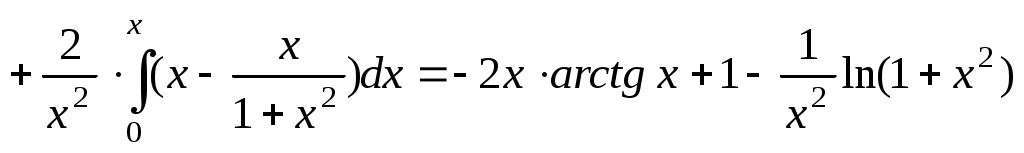 . Ответ:
. Ответ: 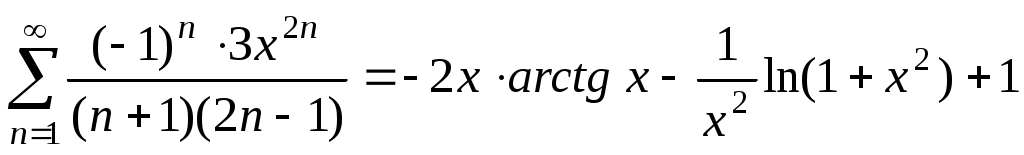 .
.
Будем искать решение уравнения в виде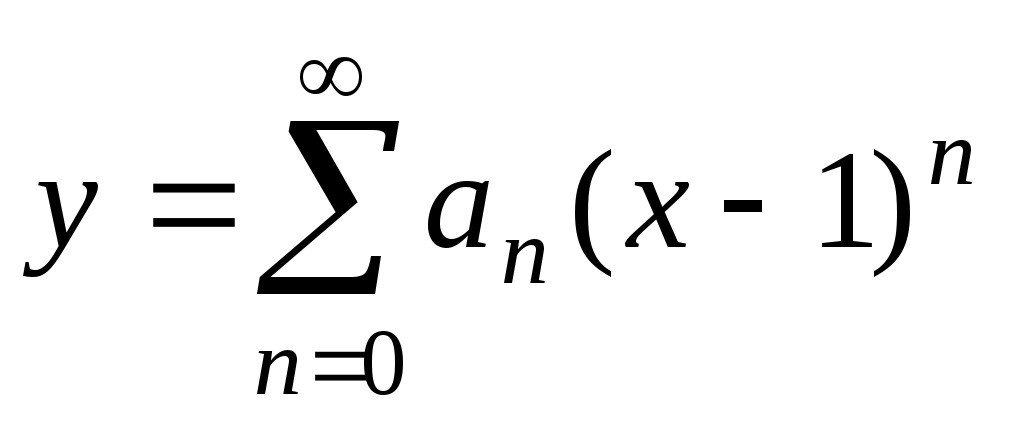 , где
, где 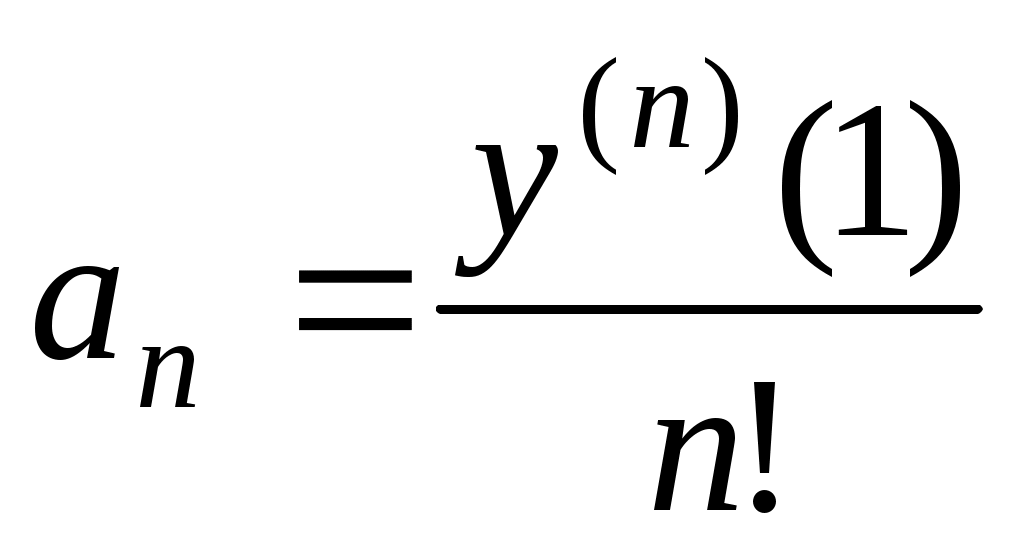 . Будем последовательно вычислять производные
. Будем последовательно вычислять производные  :
: 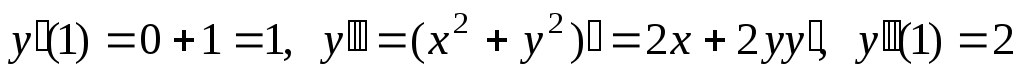 ,
, 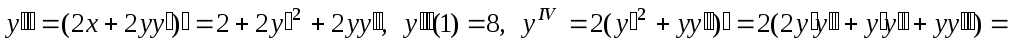
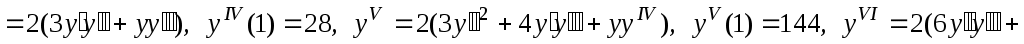
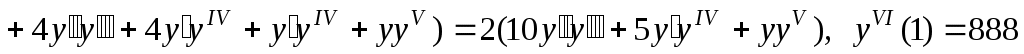 . Таким образом,
. Таким образом, 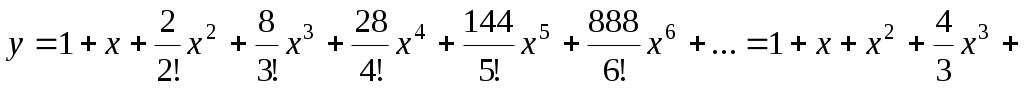
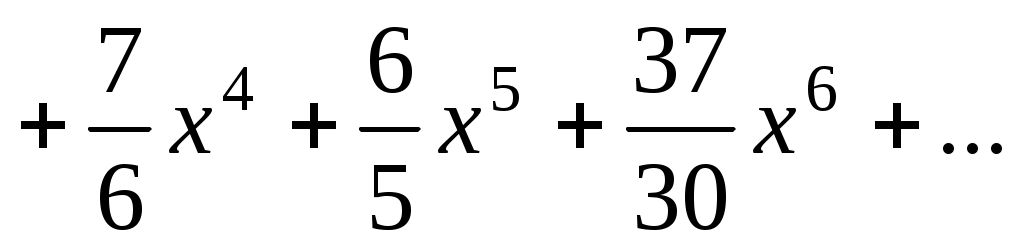 . Ответ:
. Ответ: 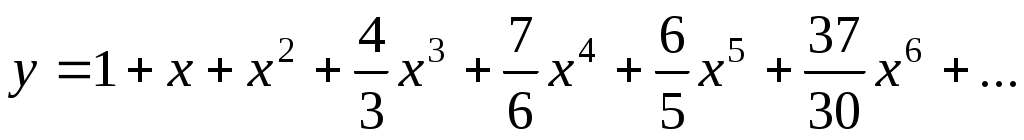 .
.
Ищем решение уравнения в виде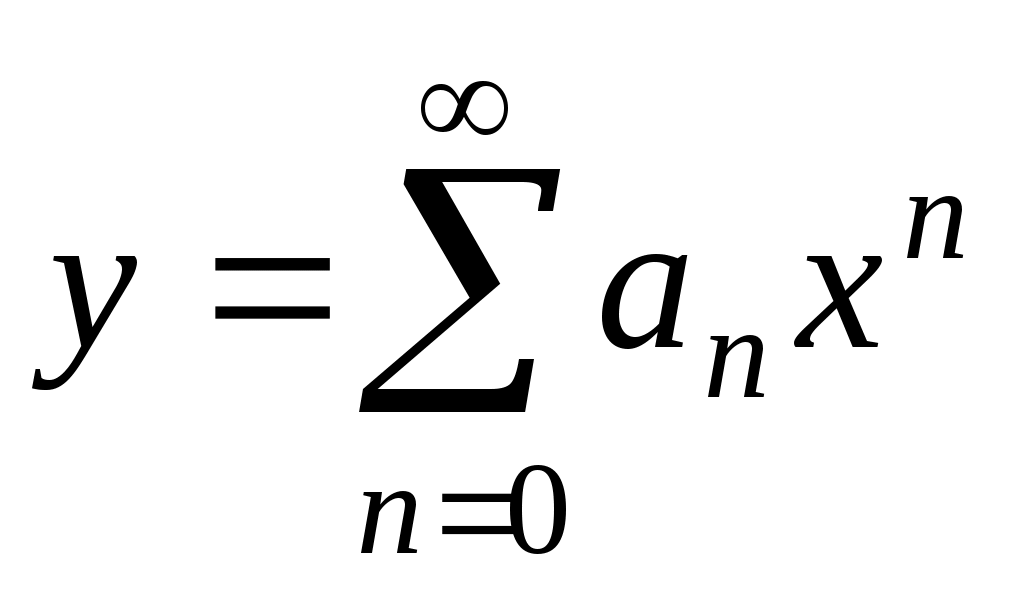 . Тогда
. Тогда 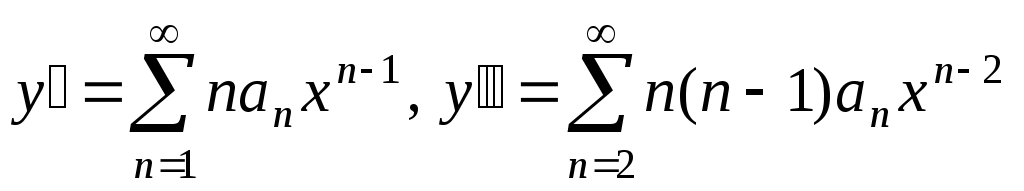 . Подставляя это в исходное уравнение, получим:
. Подставляя это в исходное уравнение, получим: 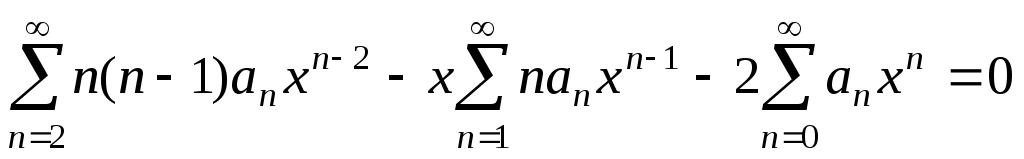 . Первую сумму можно записать в следующем виде:
. Первую сумму можно записать в следующем виде: 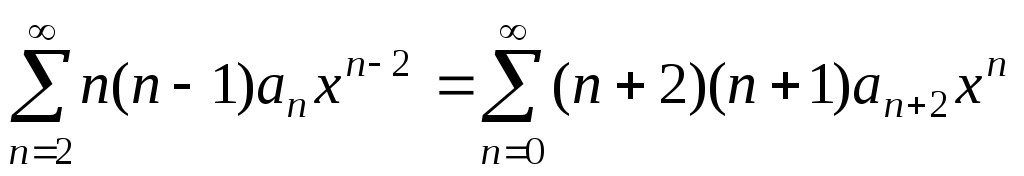 , вторую сумму – в виде
, вторую сумму – в виде 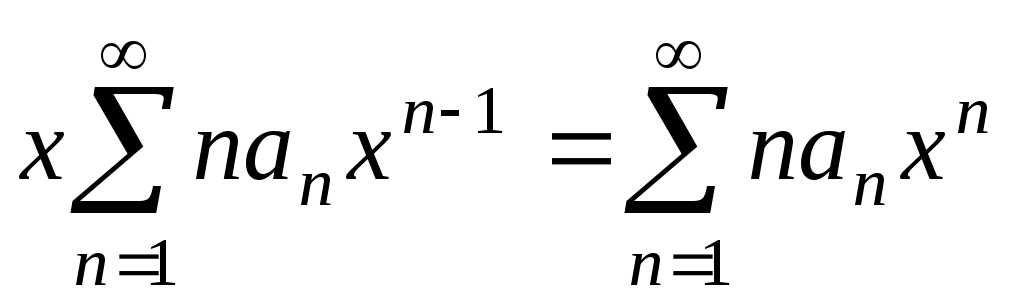 . Тогда
. Тогда 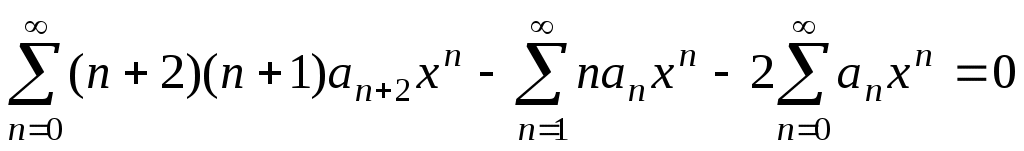
. Объединим все суммы, выделяя «лишние» слагаемые: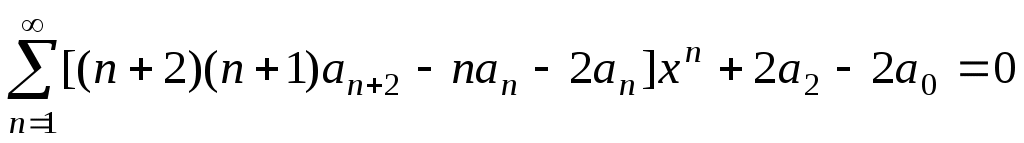 . Это равнество должно выполняться для различных значений x. Это возможно лишь тогда, когда коэффициенты при всех степенях x будут равны нулю, т.е.
. Это равнество должно выполняться для различных значений x. Это возможно лишь тогда, когда коэффициенты при всех степенях x будут равны нулю, т.е. 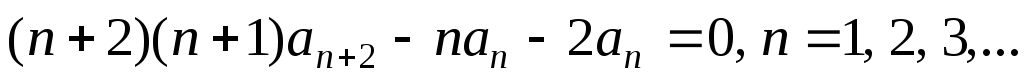 и
и 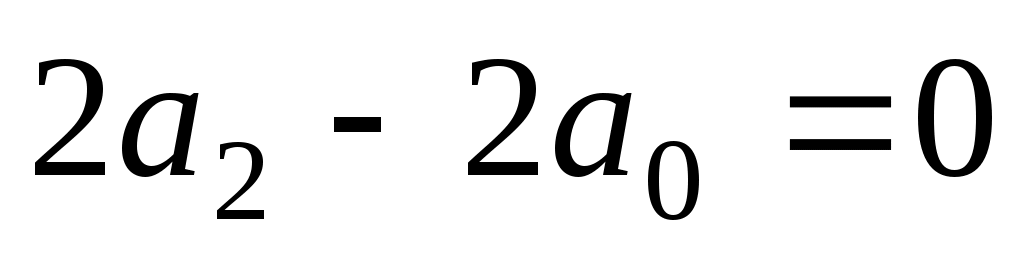 . Отсюда получаем рекуррентную формулу:
. Отсюда получаем рекуррентную формулу: 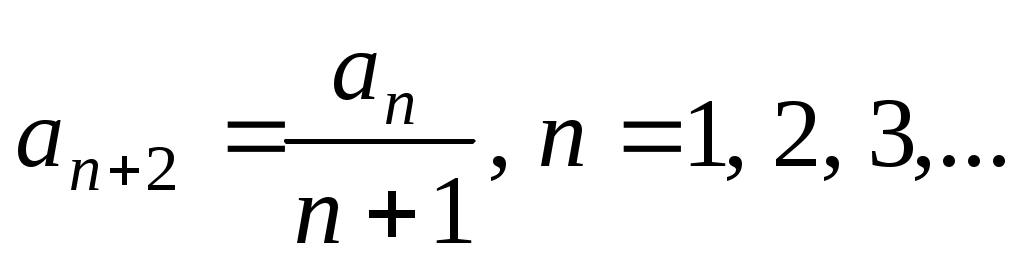 Следовательно,
Следовательно, 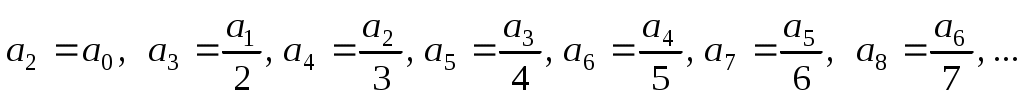 . Выразим все коэффициенты через
. Выразим все коэффициенты через 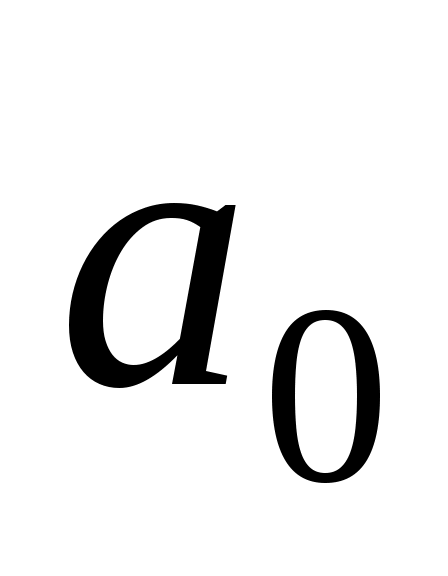 и
и 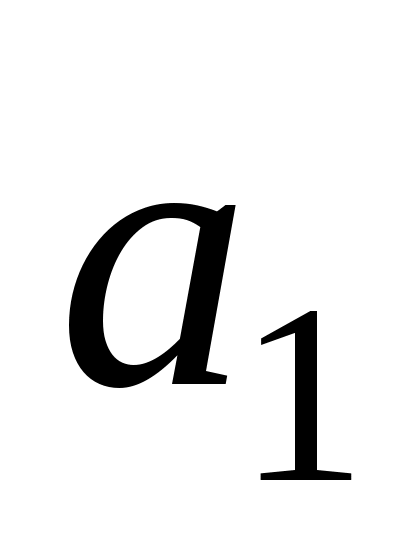 . Получим:
. Получим: 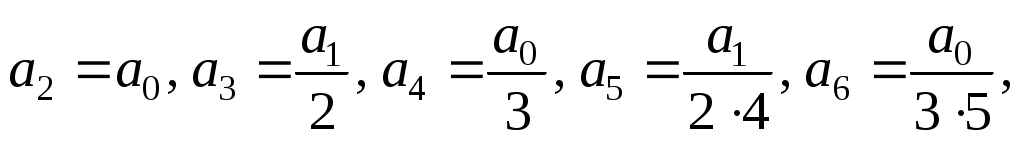
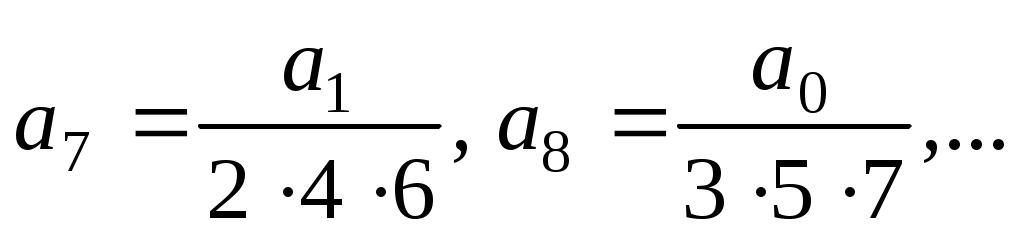 . Таким образом,
. Таким образом, 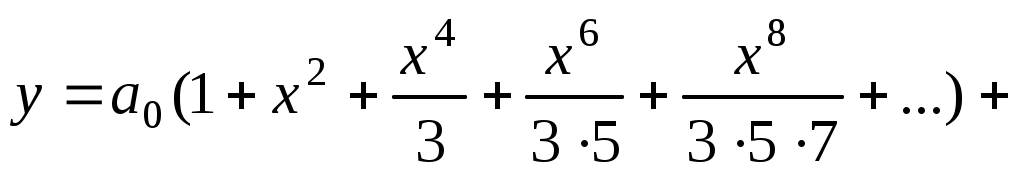
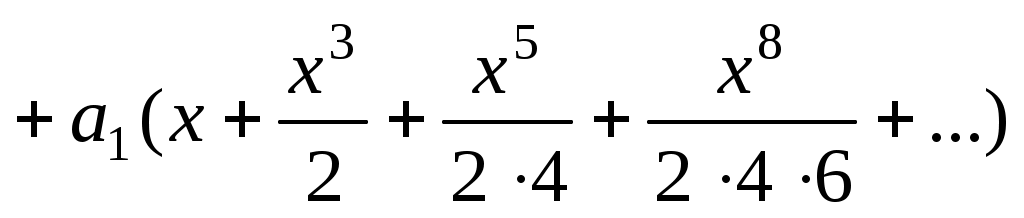 . Положим
. Положим 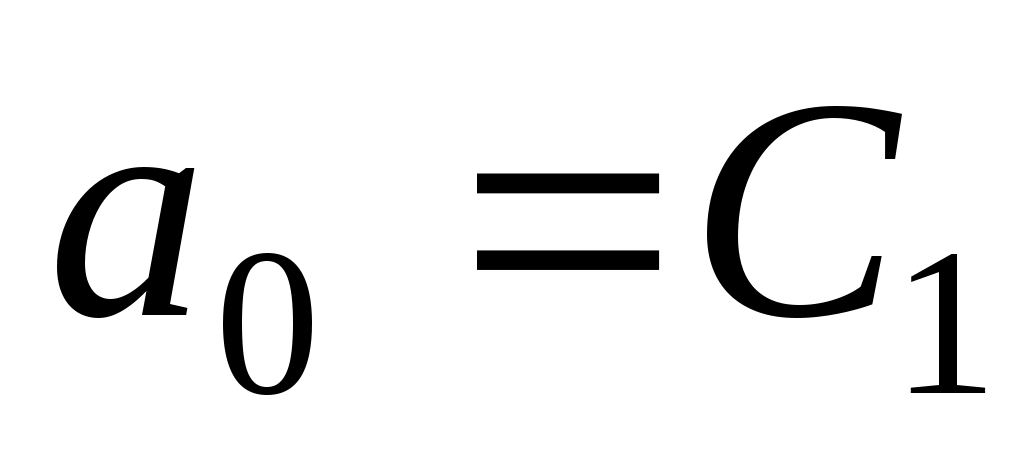 и
и 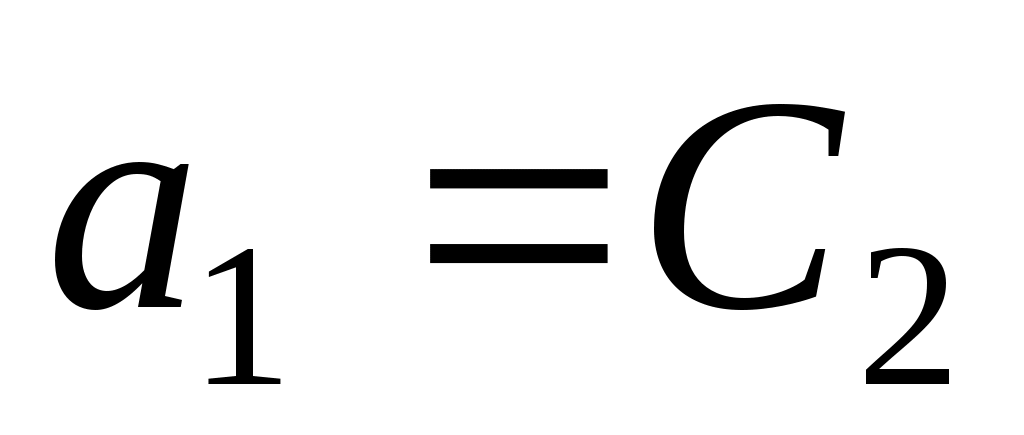 .
.
Ответ: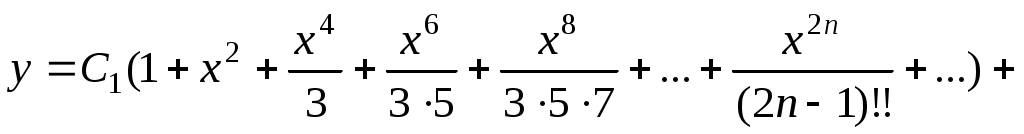
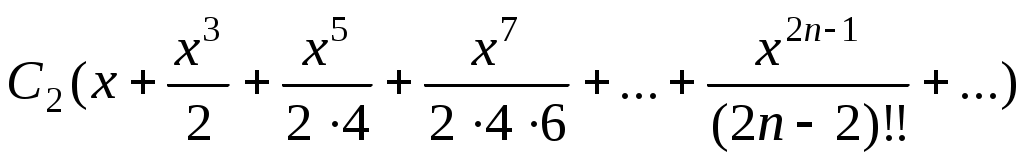 .
.
По графику определяем .
.
Ф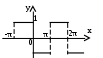
ункция является нечётной. Поэтому в разложении функции в ряд Фурье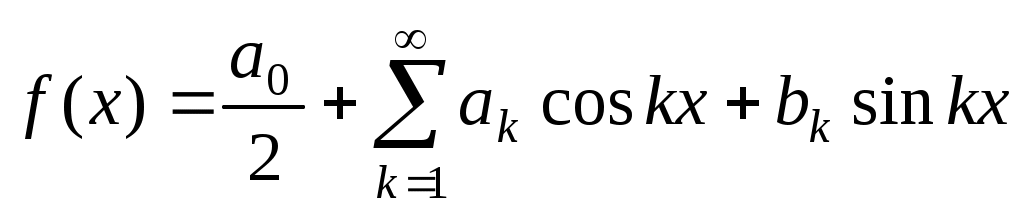 все коэффициенты
все коэффициенты 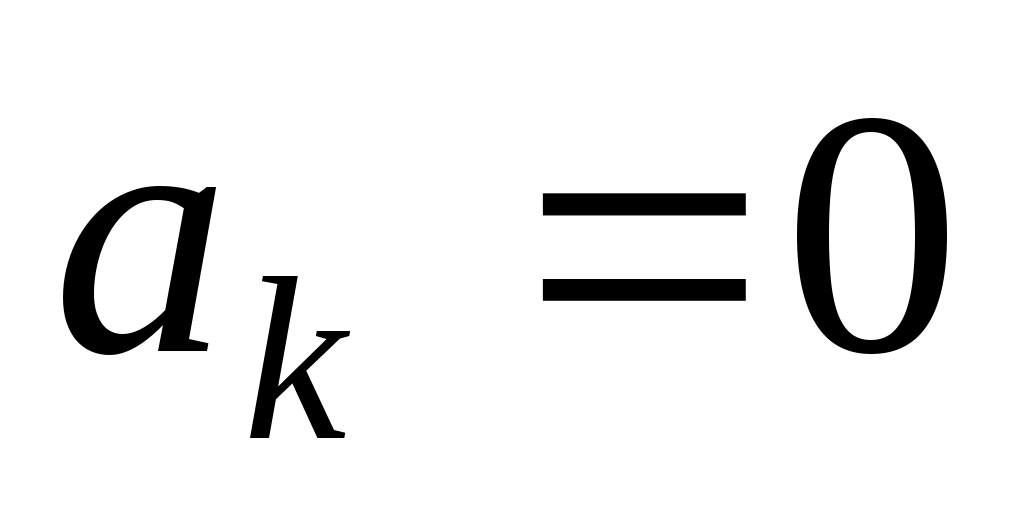 . Вычислим коэффициенты
. Вычислим коэффициенты 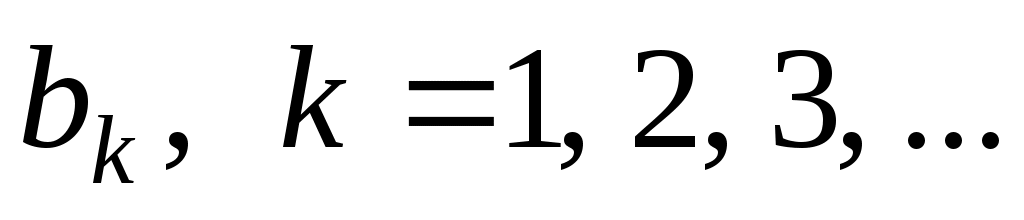 :
:  . Если
. Если 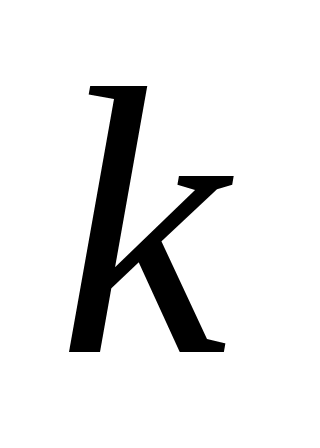 чётное, то
чётное, то
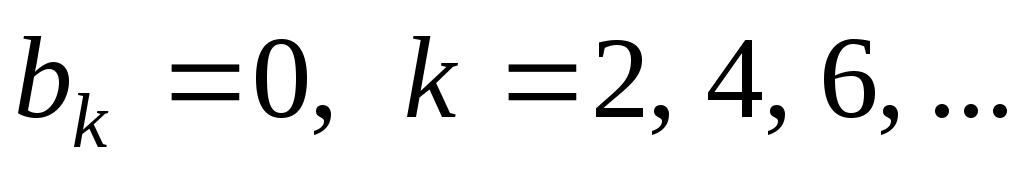 и
и 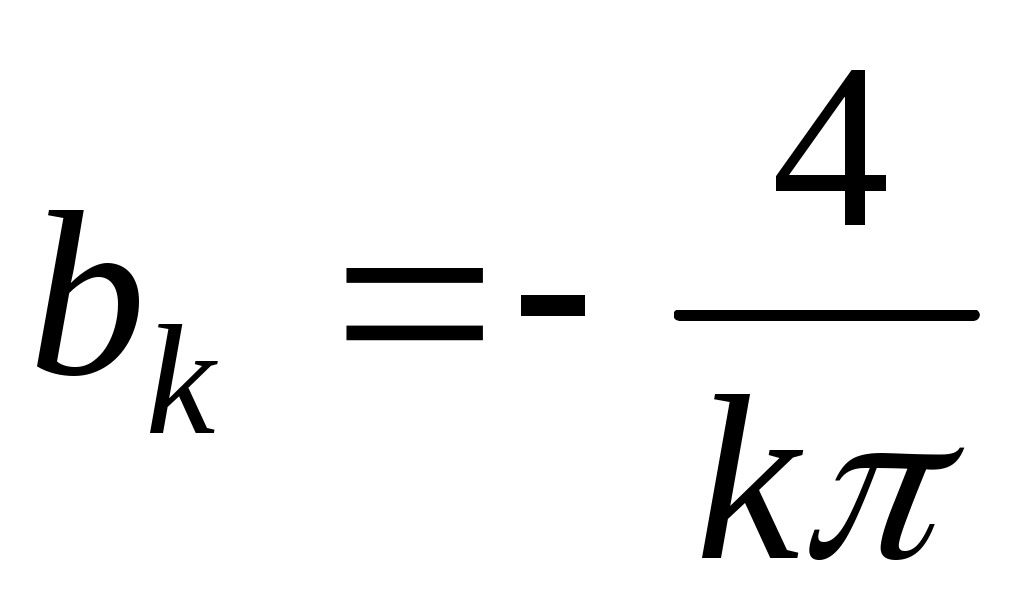 , если
, если  нечётное. Положим
нечётное. Положим 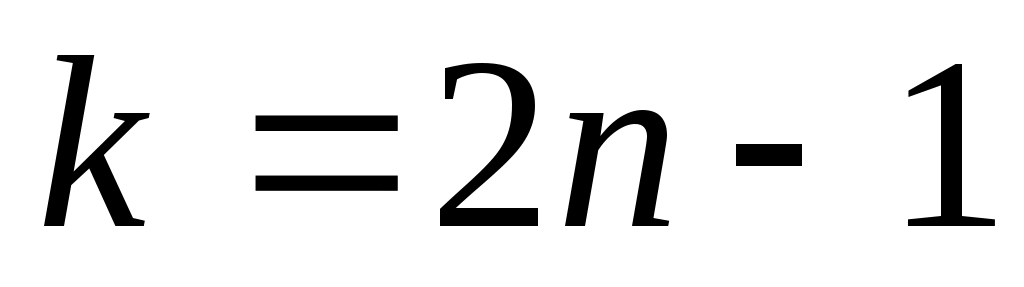 . Для нечётных
. Для нечётных  получим
получим 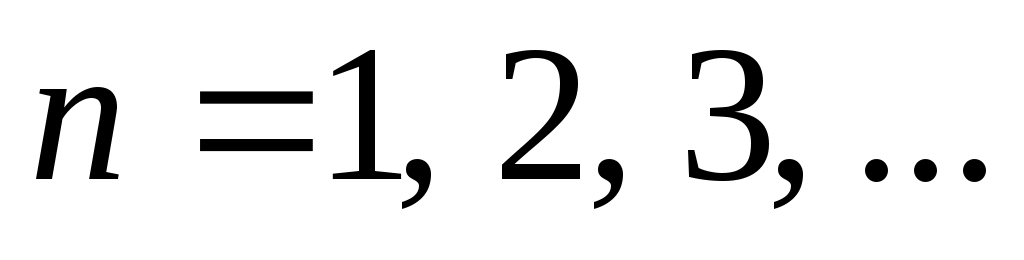 Таким образом,
Таким образом, 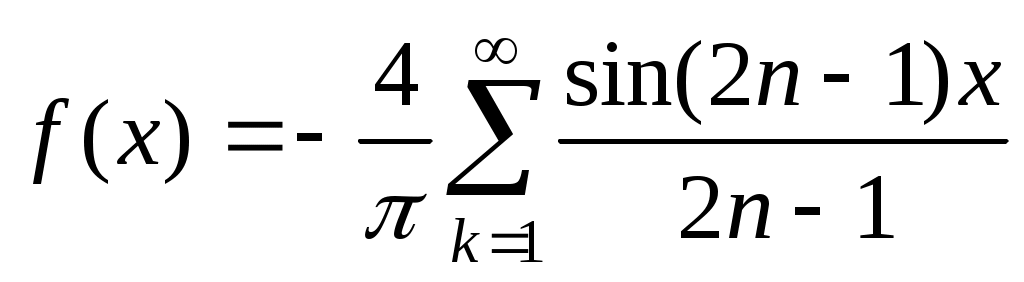 .
.
Ответ: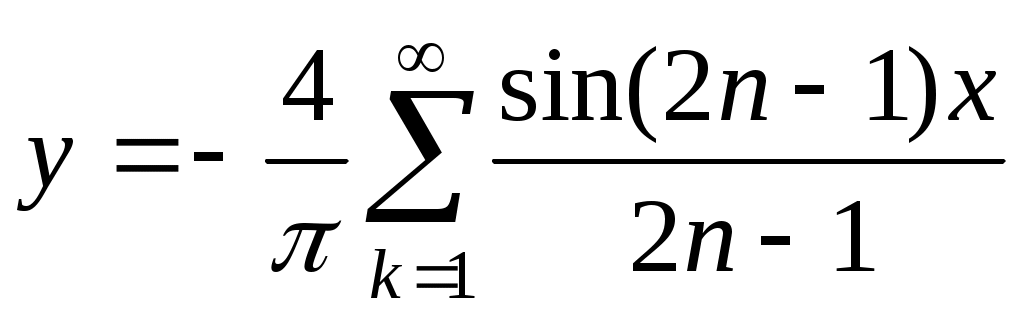 .
.
Вычисляем коэффициенты разложения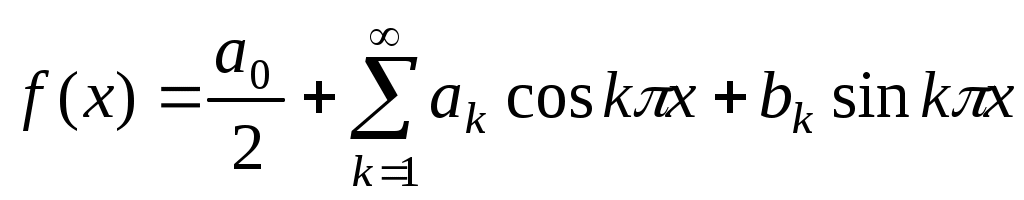 данной функции в ряд Фурье. Так как функция нечётная, то все
данной функции в ряд Фурье. Так как функция нечётная, то все 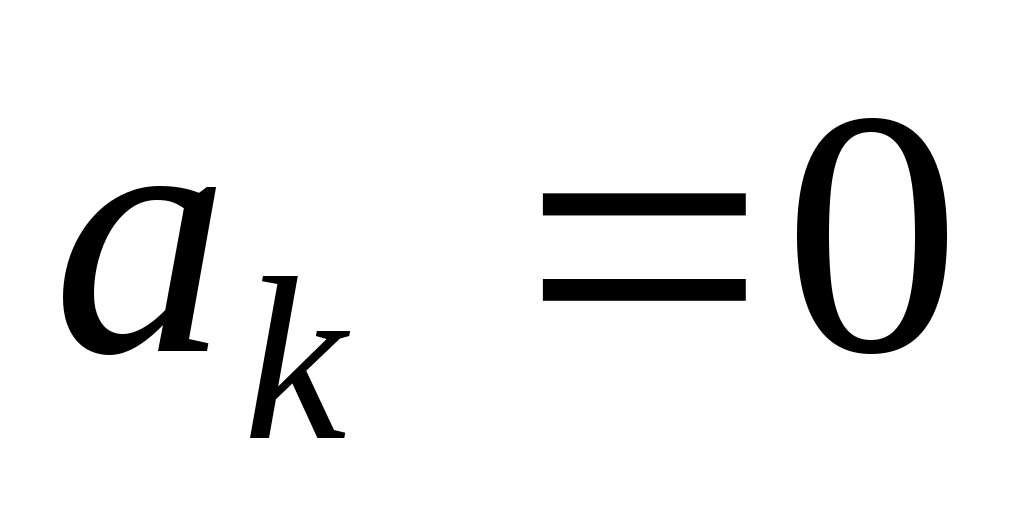 ,
, 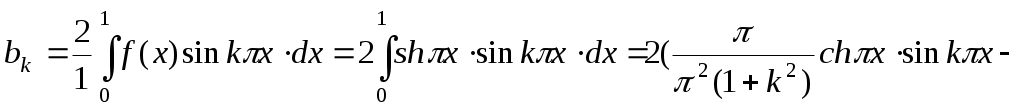
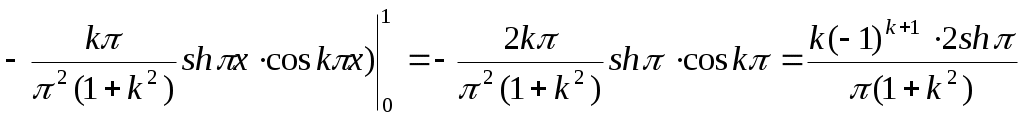 . Таким образом,
. Таким образом,
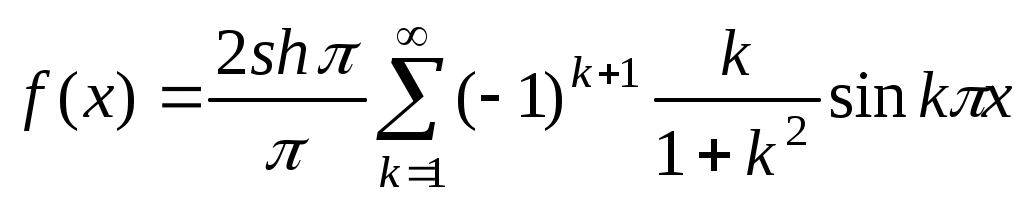 . Ответ:
. Ответ: 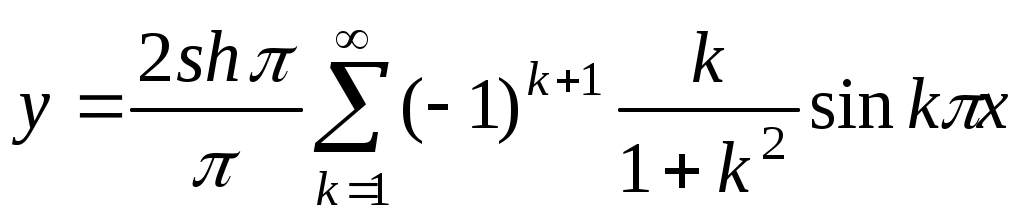 .
.
В комплексной форме ряд Фурье функции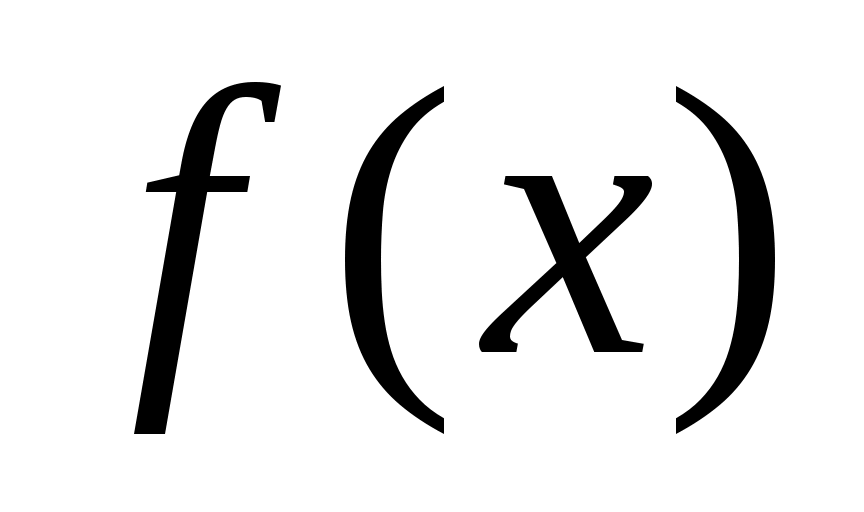 периода
периода 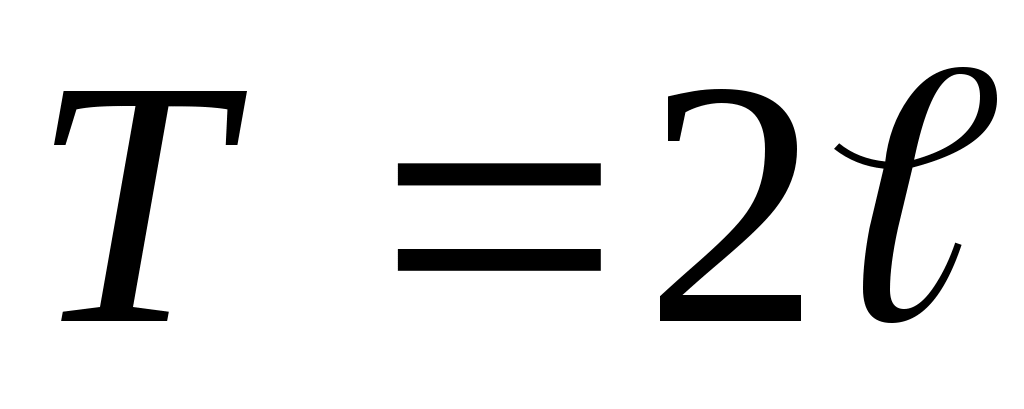 имеет вид:
имеет вид: 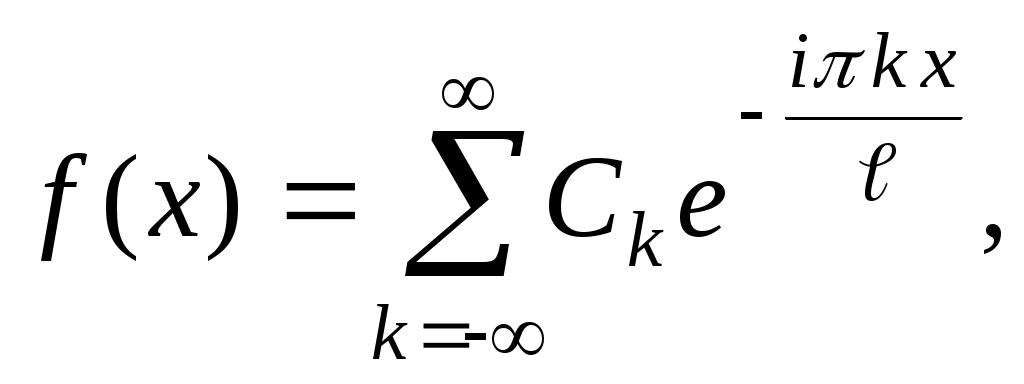 где
где 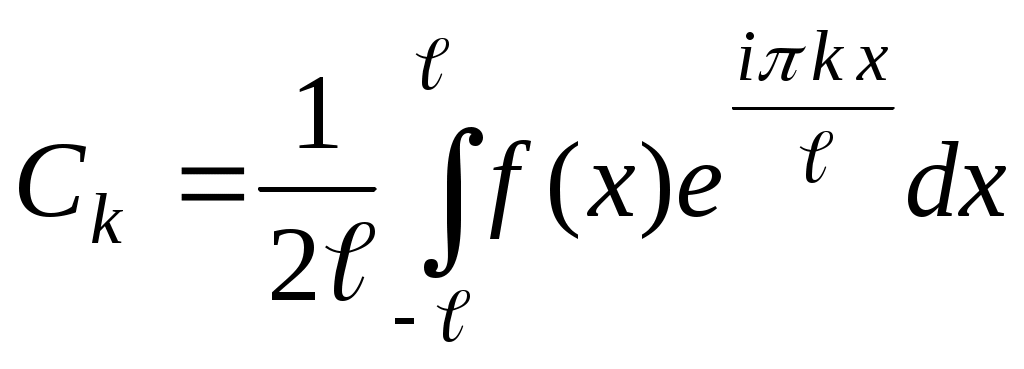 . В данном случае
. В данном случае 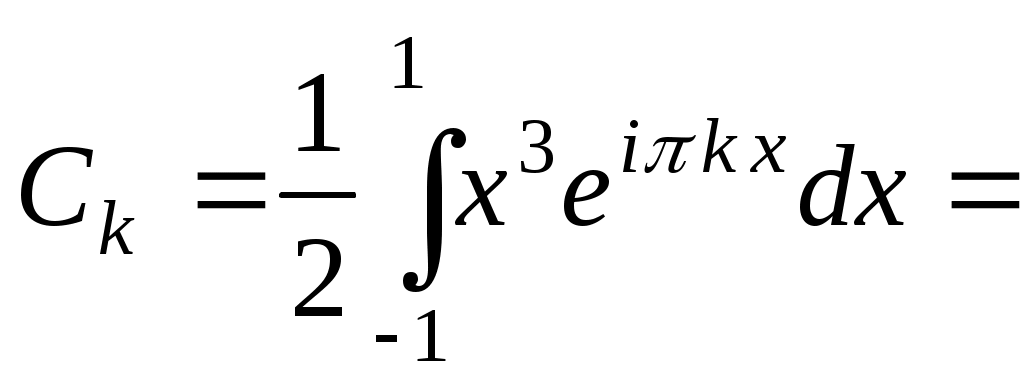
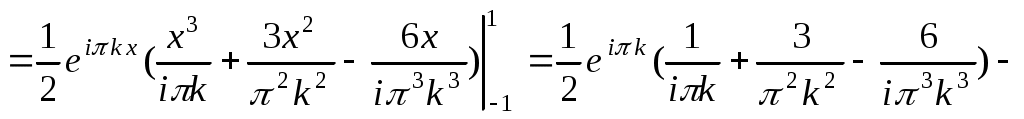
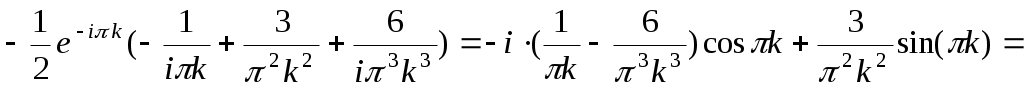
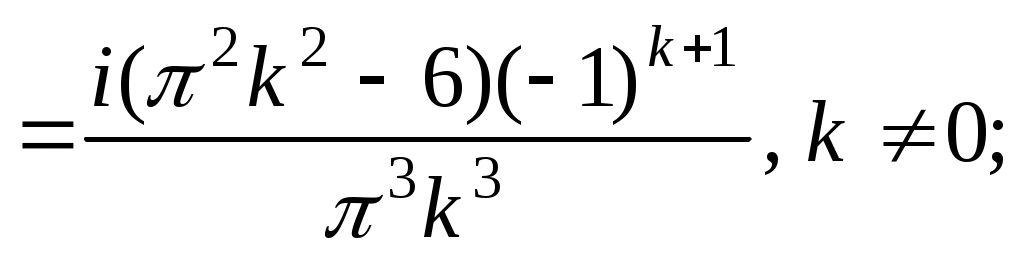
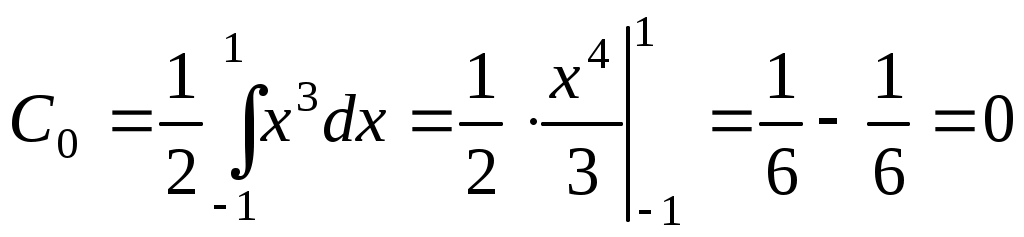 . Таким образом,
. Таким образом, 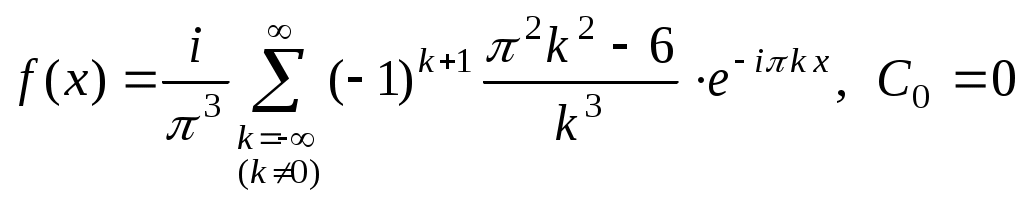 .
.
Ответ: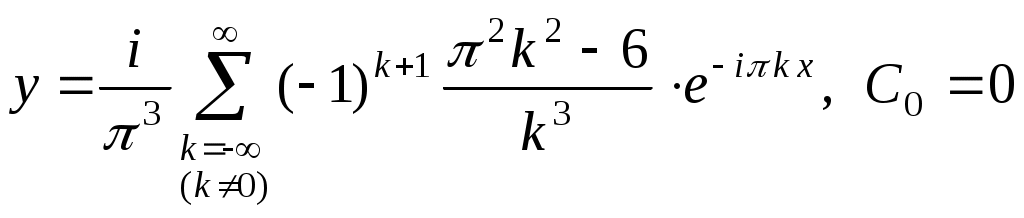 .
.
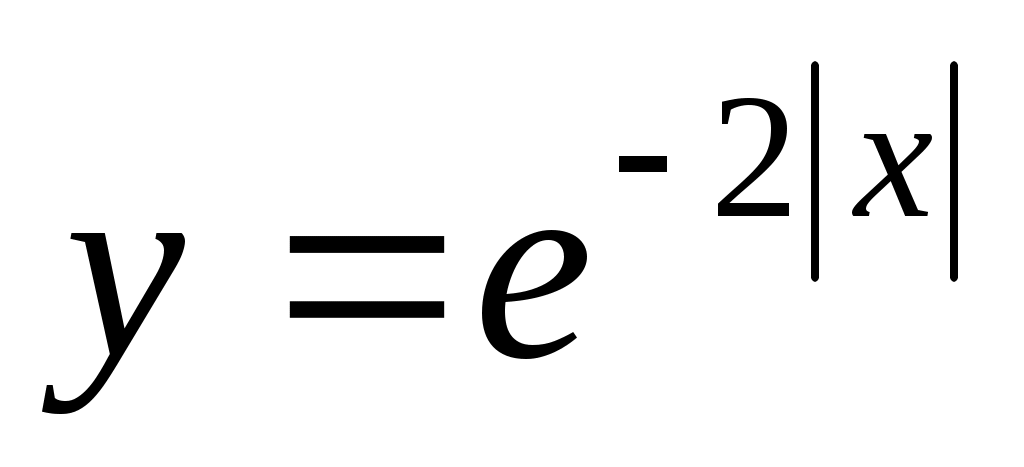 .
.
Представление функции интегралом Фурье в действительной форме имеет вид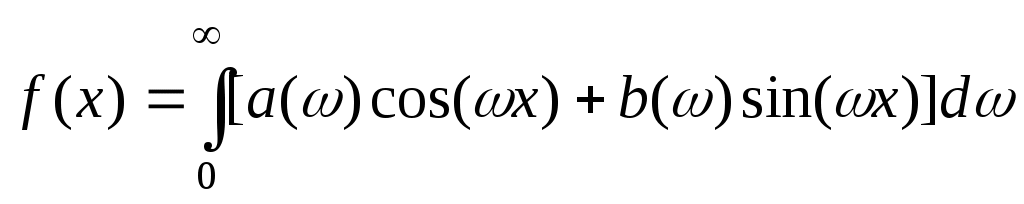 , где
, где 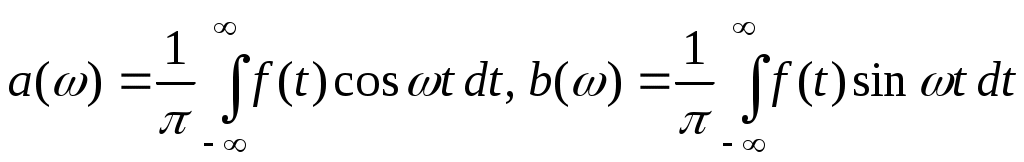 . Заданная функция является чётной и, следовательно,
. Заданная функция является чётной и, следовательно, 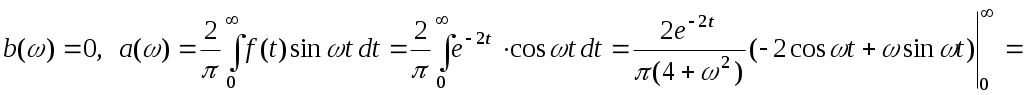
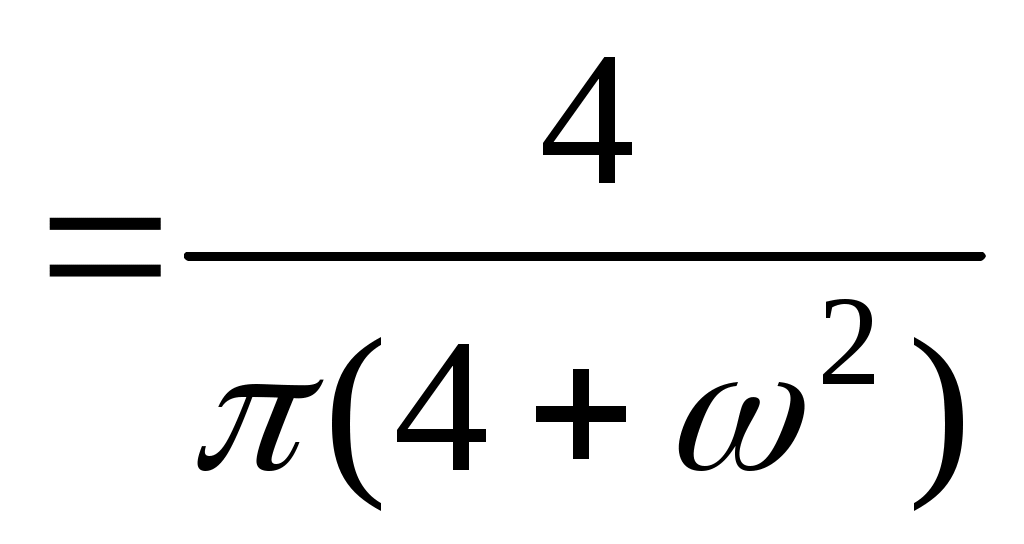 . Таким образом,
. Таким образом, 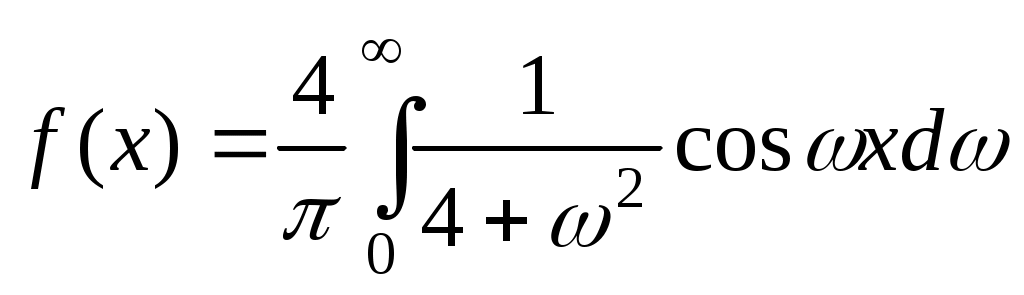 .
.
Ответ: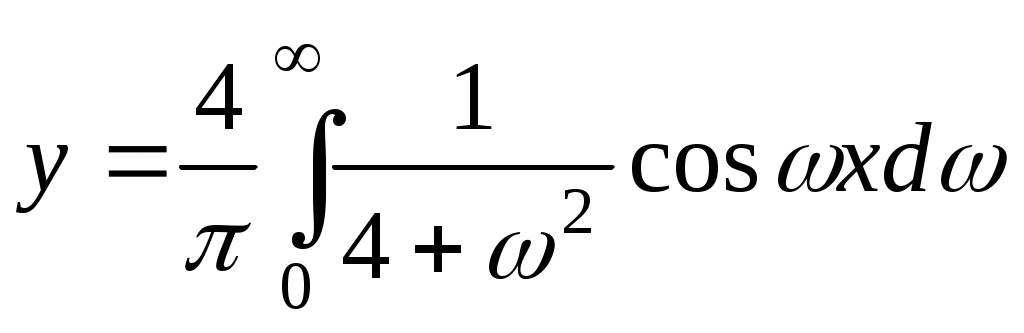
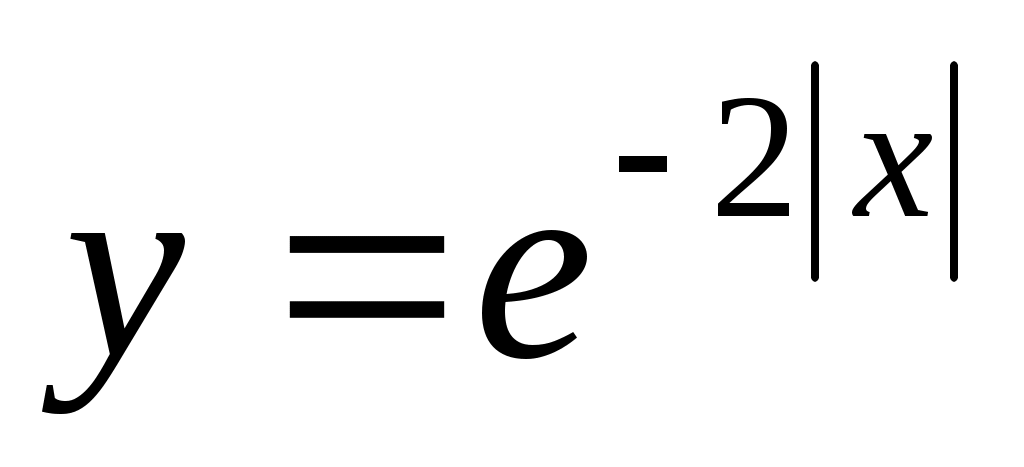 .
.
Представление функции интегралом Фурье в комплексной форме имеет вид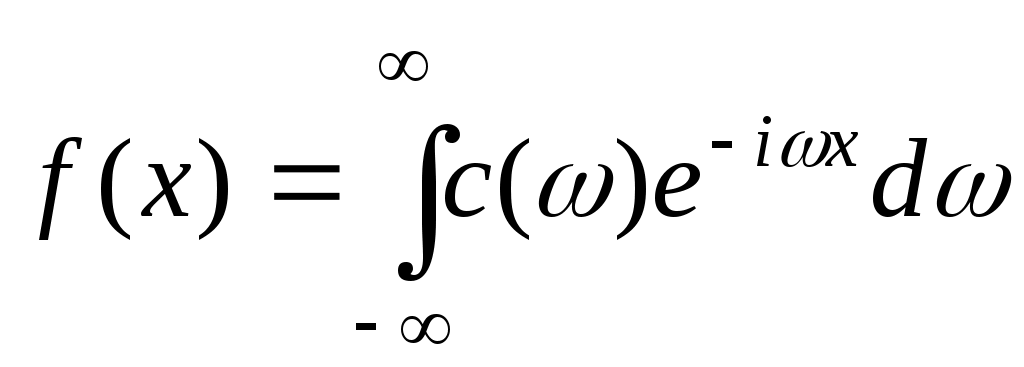 , где
, где 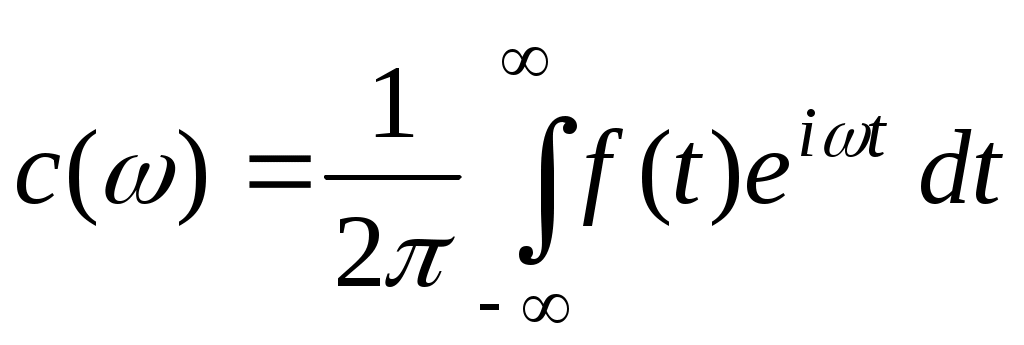 . Вычислим
. Вычислим 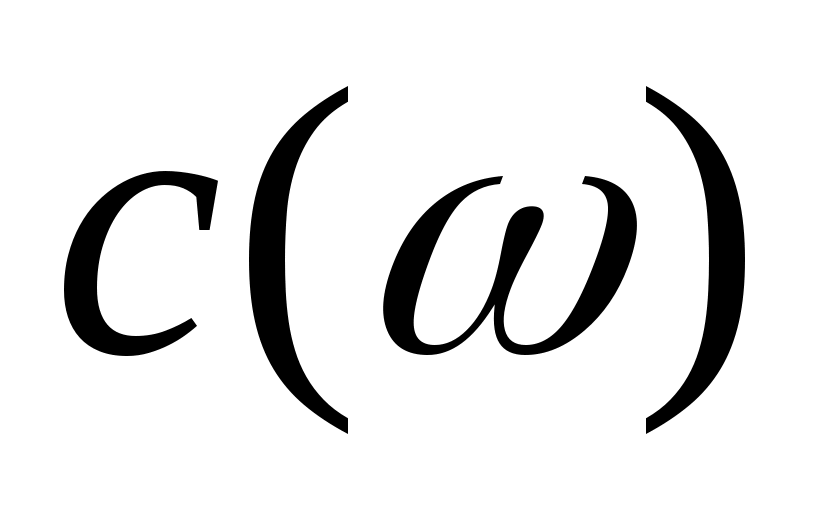 :
: 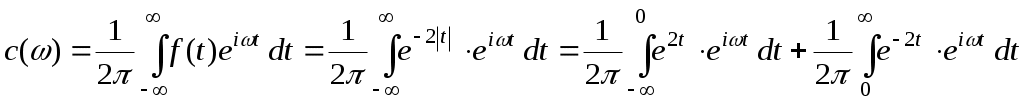
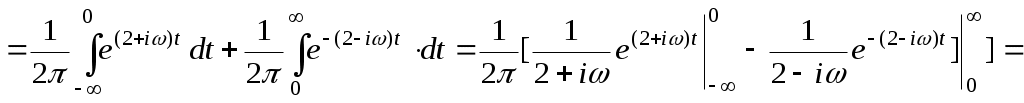
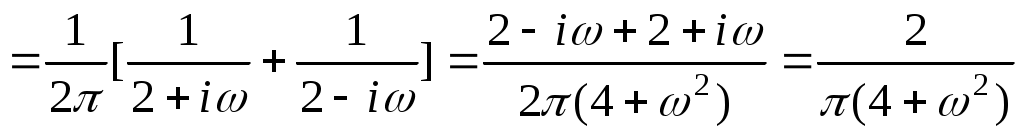 . Таким образом,
. Таким образом, 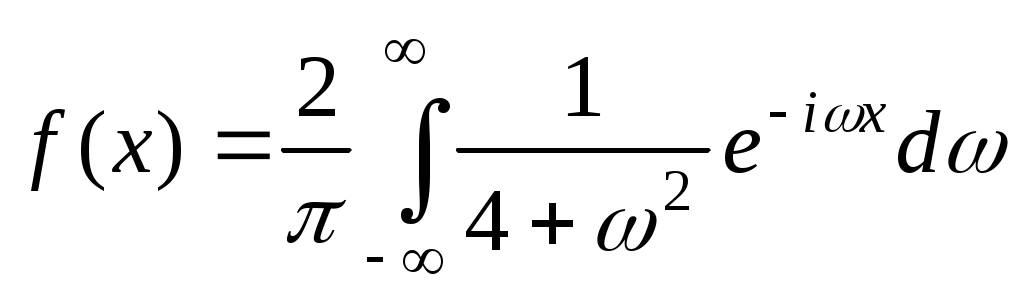 . Ответ:
. Ответ: 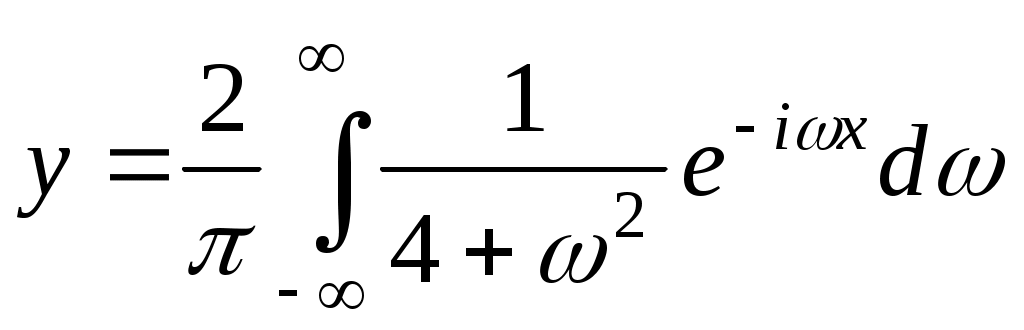
-
Вычислить предел, используя разложение функций в ряд Тейлора: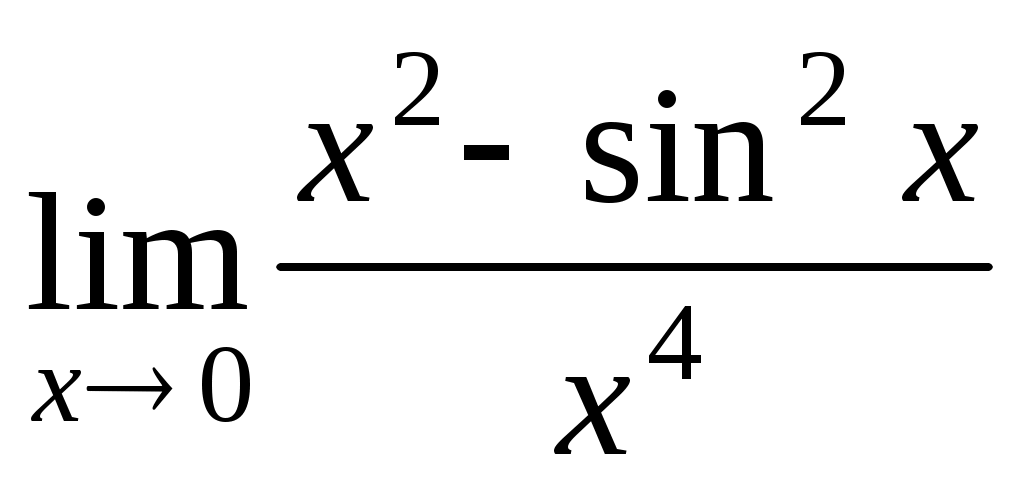 .
.
Известно, что
-
Найти сумму ряда: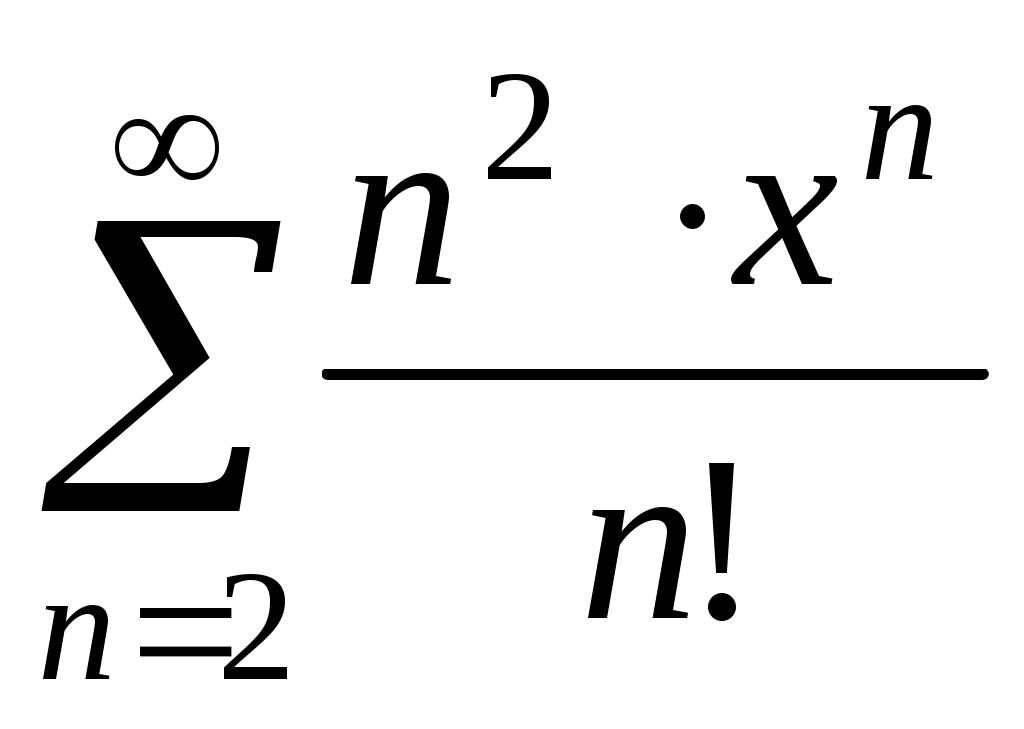 .
.
Преобразуем ряд:
-
Найти сумму ряда: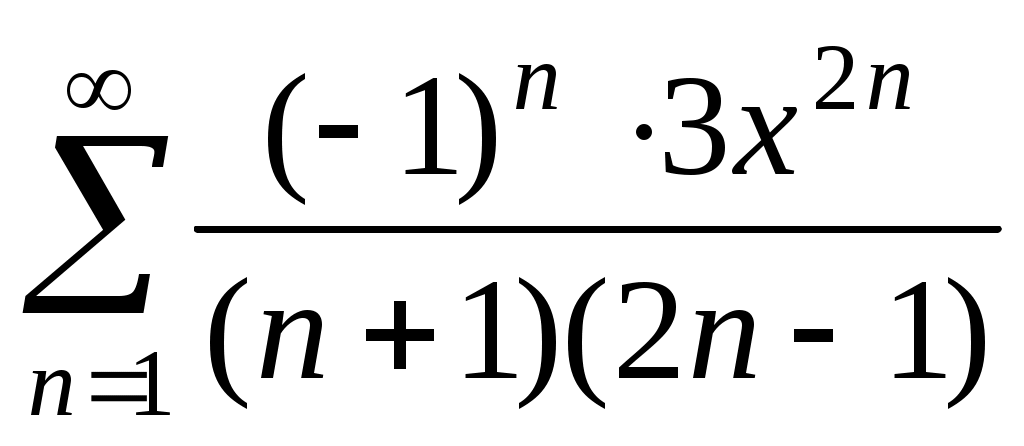 .
.
Обозначим сумму ряда через S(x). Тогда
есть суммы бесконечно убывающих геометрических прогрессий при
-
Получить решение дифференциального уравнения 1-го и 2-го порядков в виде степенного ряда или ряда Тейлора: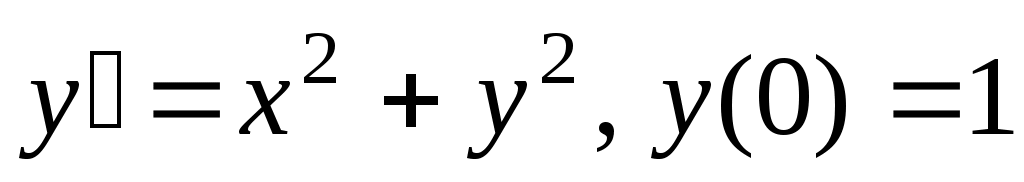
Будем искать решение уравнения в виде
-
Получить решение дифференциального уравнения 1-го и 2-го порядков в виде степенного ряда или ряда Тейлора: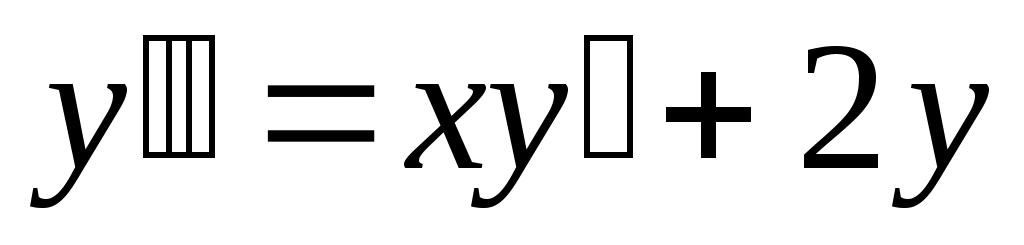
Ищем решение уравнения в виде
. Объединим все суммы, выделяя «лишние» слагаемые:
Ответ:
-
Разложить заданную графиком периодическую функцию в ряд Фурье:
По графику определяем
Ф
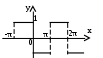
ункция является нечётной. Поэтому в разложении функции в ряд Фурье
Ответ:
-
Разложить функцию в ряд Фурье на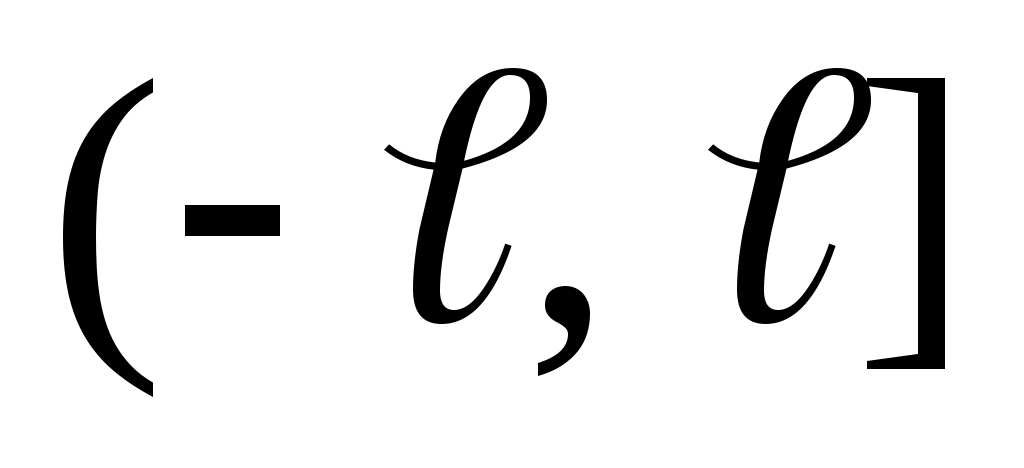 :
: 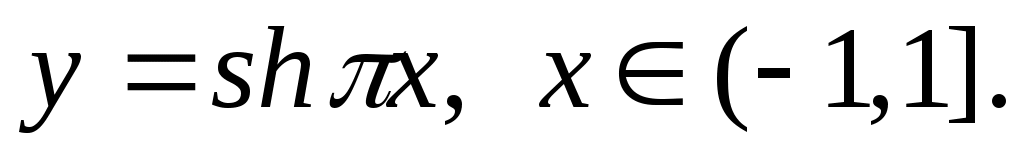
Вычисляем коэффициенты разложения
-
Найти разложение функции ряд Фурье в комплексной форме на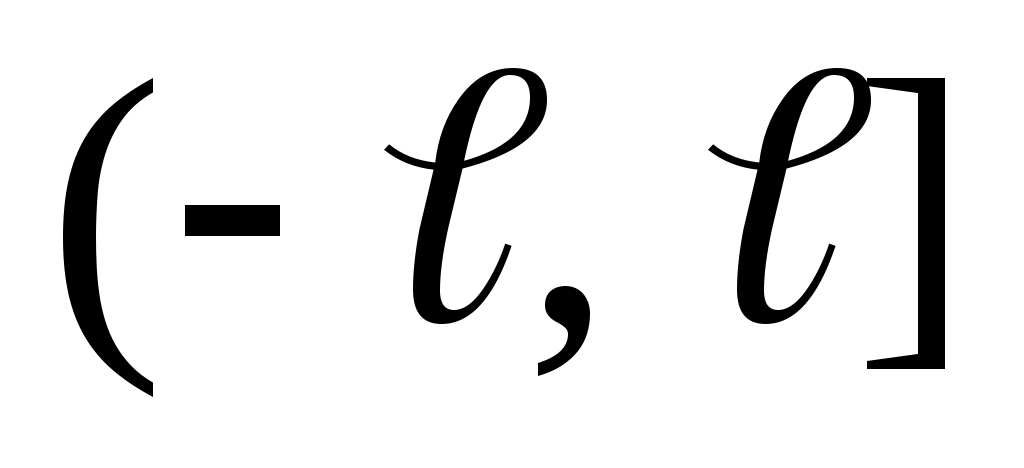 :
: 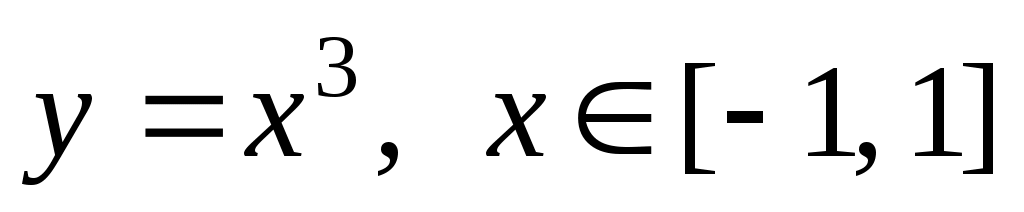 .
.
В комплексной форме ряд Фурье функции
Ответ:
-
Функцию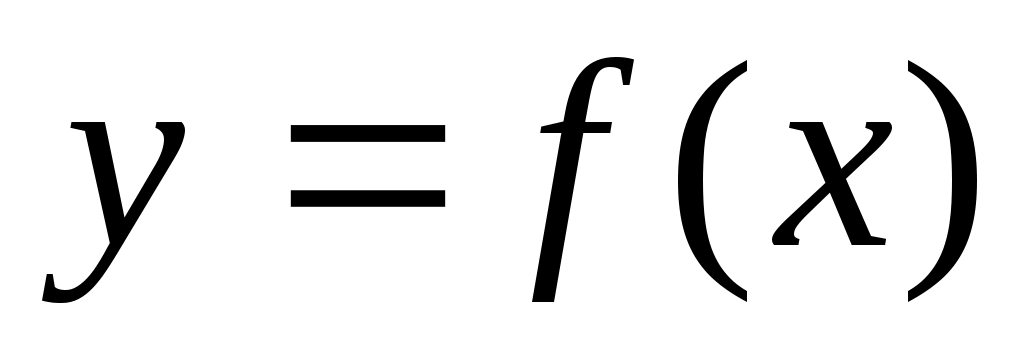 представить интегралом Фурье в действительной форме:
представить интегралом Фурье в действительной форме:
Представление функции интегралом Фурье в действительной форме имеет вид
Ответ:
-
Функцию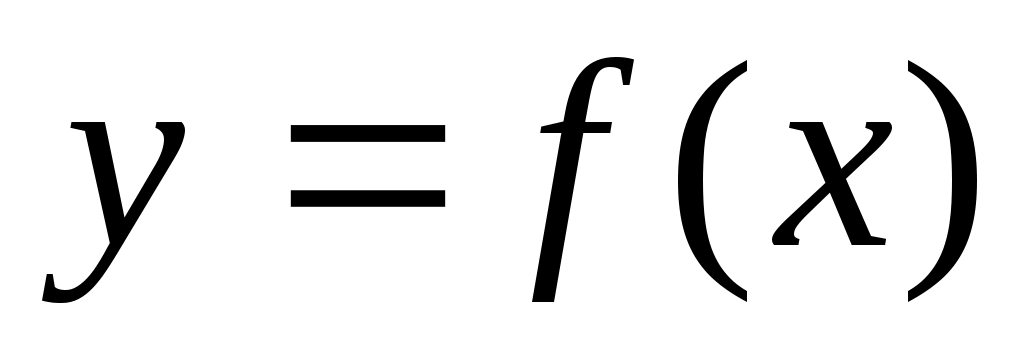 представить интегралом Фурье в комплексной форме:
представить интегралом Фурье в комплексной форме:
Представление функции интегралом Фурье в комплексной форме имеет вид