ПРИКЛАДНА КРИПТОЛОГІЯ

ЛЕКЦІЯ №2(1.2)
Тема лекції « Еліптичні криві»
Навчальні питання
2.1 Визначення еліптичних кривих .

2.2 Груповий закон для еліптичних кривих E(F(P)) в афінних координатах

2.3 Груповий закон у проективних координатах

2.4. Груповий закон для еліптичних кривих E( F(2m))

2.5 Груповий закон для еліптичних кривих E( F(3m))

2.6 Складність обчислень у різних системах координат

2.7 . Основні властивості щодо еліптичних кривих


Джерела, що рекомендуються до самостійної роботи
1. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Монографія. Харків, ХНУРЕ, Форт, 2012 р., 1 та 2 видання, 868 с.

2. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Підручник. Харків, ХНУРЕ, Форт, 2012 р., 1 видання, 878 с.

3. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний конспект лекцій. Харків, ХНУРЕ, 2012 р.

4. Горбенко І. Д. Гриненко Т. О. Захист інформації в інформаційно-телекомунікаційних системах: Навч. посібник. Ч.1. Криптографічний захист інформації - Харків: ХНУРЕ, 2004 - 368 с.

5. Горбенко Ю.І., Горбенко І.Д. Інфраструктури відкритих ключів . Системи ЕЦП. Теорія та практика. Харків. Форт. 2010 , 593с.

6. Есин В. И., Кузнєцов А. А., Сорока Л. С. Безопасность информационных систем и технологий – Х.:ООО «ЭДЭНА», 2010.-656с.

7. Горбенко І.Д., Горбенко Ю.І. Прикладна криптологія. Електронний носій до підручника. Харків, ХНУРЕ, 2012 р.

2.1 Визначення еліптичних кривих )[ 11 – 14, 47 – 49, 143 - 144 ].

Еліптичні криві над F(p^m)
Нехай F(p^m) є кінцевим полем з простим p > 3 і позитивним цілим m. Тоді існує еліптична крива E, яка описується афінним рівнянням Вейєрштраса вигляду [32]

Y² = X³ + aX + b, (1.1)

причому a, b ∈ F(p^m), якщо виконується умова що 4a³ + 27b² ≠ 0_F у полі F(p^m).

Якщо 4a³ + 27b² = 0_F у полі, то криваназивається сингулярною і не є еліптичною кривою.

Уся безліч F(p^m) - значних точок E задається як

E(F(p^m)) = {Q = (x_Q, y_Q) ∈ F(p^m) × F(p^m) | y_Q² = x_Q³ + ax_Q+ b} ∪ {0_E},

де 0_E– допоміжна точка, що називається точкою нескінченності кривої E.
Еліптичні криві над полем F(2^m)

Нехай F(2^m), для деякого m ≥ 1 буде кінцевим полем. Тоді існує еліптична крива E, яка описується афінним рівнянням Вейєрштраса вигляду [49, 143]

Y² + XY = X³ + aX² + b, 1.2)

причомуa, b∈ F(2^m), якщо тільки b≠ 0_Fу F(2^m).

У криптографічних застосунках m повинне бути простим, оскільки за таких умов забезпечується запобігання певним видам атак на криптосистему.

Якщо b = 0_F, то така крива називається сингулярною кривою і не є еліптичною кривою.

Уся безліч F(2^m) - значних точок E задається як

E (F(2^m)) = {Q = (x_Q, y_Q) ∈ F(2^m) × F(2^m) | y_Q² + x_Qy_Q = x_Q³ + ax_Q² + b} ∪ {0_E},

де 0_E– допоміжна точка, що називається точкою нескінченності кривої E.
Еліптичні криві над F(3^m)

Нехай F(3^m) буде кінцевим полем, де m – позитивне ціле. Тоді існує еліптична крива E, яка описується афінним рівнянням Вейєрштраса вигляду [49, 143]

Y² = X ³ + aX ² + b з a, b ∈ F(3^m), (1.3)

якщо a, b ≠ 0_F у полі F(3^m).

Якщо a або b = 0_F, то така крива називається сингулярною кривою і відповідно не є еліптичною кривою.

Уся безліч F(3^m) - значних точок E задається як

E (F(3^m)) = {Q = (x_Q, y_Q) ∈ F(3^m) × F(3^m) | y_Q² = x_Q³ + ax_Q² + b} ∪ {O_E},

де O_E – допоміжна точка, що називається точкою на нескінченності E.

2.2 Груповий закон для еліптичних кривих E(F(P)) в афінних координатах

Огляд систем координат

Зазвичай еліптична крива визначається в афінних координатах. Тому базова точка або відкритий ключ користувача задається в афінних координатах. Головним недоліком афінних координат є складність операції ділення в полі F(q) при виконанні як складання, так і подвоєння [49]. Зменшення складності в цілому при складанні та подвоєнні точок може досягатись засобом уникнення операції ділення, причому якомога більше. Це досягається використанням при множенні (складанні та подвоєнні точок) інших координат, таких як проективні координати, координати Якобі та модифіковані координати Якобі тощо, які є трьохмірними [49, 143]. Причому має забезпечуватись вимога, щоб усі і системи координат, що використовуються, були сумісні.
Груповий закон в афінних координатах

Нехай F(q) є кінцевим полем Галуа з p > 3. Нехай E є еліптичною кривою над F(q), що задається «коротким рівнянням Вейєрштраса » [49],

Y² = X³ + aX + b, a, b ∈ F(q), (1.4)

а також 4a³ + 27b² ≠ 0_F у полі F(q). Тоді в афінних координатах груповий закон складання та подвоєння на еліптичній кривій (1.4) задається таким чином:

1. 
   точка на нескінченності O_E є одиничним елементом до операції додавання «+»;
   
2. 
   усі точки R = (x, y) є такими, що R ≠ O_E;
   
3. 
   якщо R₁ = (x₁, y₁) і R₂ = (x₂, y₂) є дві різні точки на E – такі, що R₁ ≠ ± R₂ і R₁, R₂ ≠ O_E, то сумою точок R₁ та R₂ є точка R₃ = (x₃, y₃), координати якої визначаються як:
   

x₃ = r² – x₁ – x_2;

y₃ = r (x₁ – x₃) – y_{1, (1.5)}

r = (y₂ – y₁) / (x₂ – x₁);

4. 
   якщо R = (x, y) є точка на E – така, що R ≠ 0_Eі y ≠ 0_F, то її подвоєнням є точка 2R = (x₃, y₃), координати якої визначаються як:
   

x₃ = r² – 2x;

y₃ = r (x – x₃) – y, (1.6)

r = (3x² + a) / (2y).

У разі якщо R = (x, 0_F), подвоєнням цієї точки є точка 2R = 0_E.

Геометрична інтерпретація складання двох точок з координатами (х1, у1) та (х2, у2) на еліптичній кривій наведено на рис .2.1





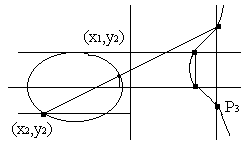
Рис.2.1 Геометрична інтерпретація складання двох точок.


2. 3 Груповий закон у проективних координатах

Особливістю проективного базису є те, що при використанні проективних координат необхідно виконувати більше операцій множення, але немає операції ділення за модулем (інверсії). Після виконання скалярного множення в проективному базисі необхідно зробити зворотне перетворення на афінні координати. Але при виконанні перетворення з проективних координат на афінні, необхідне одне ділення в полі.

Проективний аналог короткого афінного рівняння Вейєрштраса (1.4) визначається однорідним кубічним рівнянням [49]

Y²Z = X³ + aXZ² + bZ³, a, b ∈ F(q). (1.7)

Безліч усіх трійок еквівалентна (X, Y, Z) і позначається як (X, Y, Z)/

.

Еліптична крива, що задається в проективних координатах, складається з усіх точок R = (X, Y, Z) рівняння (1.7) так, що трійка (X, Y, Z) є рішенням рівняння.

Існує співвідношення між точками Q кривої E, коли крива задана в афінних координатах, а точка R – у проективних координатах. У цьому випадку справедливі твердження:

1. 
   Якщо Q = (X_Q, Y_Q) є точка в афінних координатах, то R = (X_Q, Y_Q, 1_F) є відповідною точкою в проективних координатах.
   
2. 
   Якщо R = (X, Y, Z) (з Z ≠ 0_F) є рішенням (1.7), то Q = (X/Z, Y/Z) є відповідною точкою в афінних координатах кривої E.
   
3. 
   Існує тільки одне рішення (1.7) із Z = 0, а саме: точка (0_F, 1_F, 0_F), яка відповідає 0_E.
   

У проективних координатах груповий закон задається таким чином:

1. 
   точка (0_F, 1_F, 0_F) є одиничним елементом 0_Eвідносно операції «+»;
   
2. 
   точка R = (X, Y, Z) ≠ (0_F, 1_F, 0_F) є точкою на E, що задана в проективних координатах, тоді точка – R = (X, – Y, Z);
   
3. 
   нехай R₁ = (X₁, Y₁, Z₁) і R₂ = (X₂, Y₂, Z₂) є дві відмінні точки на E – такі, що R₁ ≠ R₂ і R₁, R₂ ≠ (0_F, 1_F, 0_F), тоді сума R₁ та R₂ є R₃ = (X₃, Y₃, Z₃). Координати X₃, Y₃ і Z₃ можуть бути обчисленні за допомогою таких формул:
   

X₃ = –su,

Y₃ = t (u + s²X₁Z₂) – s³Y₁Z₂, (1.8)

Z₃ = s³Z₁Z₂,

де

s = X₂Z₁ – X₁Z₂, t = Y₂Z_{1 –} Y₁Z₂, і u = s² (X₁Z₂ + X₂Z₁) – t²Z₁Z₂.

4. 
   якщо R = (X, Y, Z) ≠ (0_F, 1_F, 0_F) є точкою на E, тодіїї подвоєння є 2R = (X₃, Y₃, Z₃).
   

Координати точки 2R – (X₃, Y₃, Z₃) можуть бути обчислені за допомогою таких формул:

X₃ = –su,

Y₃ = t (u + s²X) – s³Y, (1.9)

Z₃ = s³Z,

де

t = 3X² + aZ², s = 2YZ і u = 2s²X – t²Z.
Груповий закон у проективних координатах Якобі

Особливістю групового закону в проективних координатах Якобі є те, що скалярне множення вимагає більше множень, але не вимагає обчислення інверсій.

Аналогом рівняння Якобі в проективних координатах відносно короткого рівняння Вейєрштраса (1.5) є кубічне рівняння [49]

(Jac) Y² = X³ + aXZ⁴+ bZ⁶, a, b ∈ F(q). (1.10)

Безліч усіх трійок еквівалентна (X, Y, Z) і позначається як (X, Y, Z)/.

Існує відношення між точками Q кривої E, коли крива задана в афінних координатах, а точки R – у проективних координатах. Так, справедливими є твердження:

1. 
   Якщо Q = (X_Q, Y_Q) є точкою в афінних координатах E, то R = (X_Q, Y_Q, 1_F) є відповідною точкою в координатах Якобі.
   
2. 
   Якщо R = (X, Y, Z) (Z ≠ 0_F) є рішенням (1.10), тобто в координатах Якобі, то Q = (X/Z², Y/Z³) є відповідною точкою в афінних координатах точки E.
   
3. 
   Існує тільки одне рішення (1.10) зі значенням Z = 0_F, а саме точка (1_F, 1_F, 0_F), яка відповідає 0_E.
   

У проективних координатах Якобі груповий закон для (1.10) задається таким чином [49]:

1. 
   точка (1_F, 1_F, 0_F) є одиничним елементом 0_Eщодо «+»;
   
2. 
   якщо R = (X, Y, Z) ≠ (1_F, 1_F, 0_F) є точкою на E, заданою в координатах Якобі, тоді точка – R = (X, – Y, Z);
   
3. 
   якщо R₁ = (X₁, Y₁, Z₁) і R₂ = (X₂, Y₂, Z₂) є дві відмінні точки на E, але такі, що R₁ ≠ R₂ і R₁, R₂ ≠ (1_F, 1_F, 0_F), тоді сумою точок R₁ та R₂ є точка R₃ = (X₃, Y₃, Z₃). Координати X₃, Y₃ і Z₃ можуть бути обчислені за допомогою таких формул:
   

X₃ = – h³ – 2u₁h² + r²,

Y₃= – s₁h³ + r (u₁h² – X₃), (1.11)

Z₃ = Z₁Z₂h,

де

u₁ = X₁Z²₂, u₂ = X₂Z²₁, s₁ = Y₁Z³2, s₂ = Y₂Z³₁, h = u₂ – u₁, і r = s₂ – s₁;

4. 
   якщо R = (X, Y, Z) ≠ (1_F, 1_F, 0_F) є точкою на E, тодіїї подвоєння є 2R = (X₃, Y₃, Z₃). Координати X₃, Y₃ і Z₃ можуть бути обчислені за допомогою таких формул:
   

X₃ = t,

Y₃ = – 8Y⁴ + m (s – t),

Z₃ = 2YZ,

де

s = 4XY², m = 3X² + aZ⁴ і t = – 2s + m².
Груповий закон у модифікованих координатах Якобі

Згідно з тим же кубічним рівнянням (1.10) груповий закон у модифікованих координатах Якобі задається шляхом представлення координат Якобі четвіркою координат (X, Y, Z, aZ⁴). Таке представлення забезпечує найменшу складність операції подвоєння для еліптичної кривої E (F(q)).

У модифікованих координатах Якобі груповий закон на еліптичній кривій задається таким чином [49]:

1. 
   якщо R₁ = (X₁, Y₁, Z₁, aZ⁴₁) і R₂ = (X₂, Y₂, Z₂, aZ⁴₂) є дві відмінні точки на E – такі, що R₁ ≠R₂ і R₁, R₂ ≠ (1_F, 1_F, 0_F, 0_F), тоді сумою є точка R₃ = (X₃, Y₃, Z₃, aZ⁴₃). Координати X₃, Y₃ і Z₃ можуть бути обчислені за допомогою таких формул:
   

X₃ = – h³ – 2u₁h² + r²,

Y₃ = – s₁h³ + r (u₁h² – X₃), (1.13)

Z₃ = Z₁Z₂h,

aZ⁴₃ = aZ⁴₃,

де

u₁ = X₁Z²₂, u₂ = X₂ Z²₁, s₁ = Y₁Z³₂, s₂ = Y₂ Z³₁, h = u₂ – u₁, і r = s₂ – s₁;

2. 
   якщо R = (X, Y, Z, aZ⁴) ≠ (1_F, 1_F, 0_F, 0_F) є точкою на E, тодіїї подвоєння позначається як 2R = (X₃, Y₃, Z₃, aZ⁴ ₃). Координати X₃, Y₃ і Z₃ можуть бути обчислені за допомогою формули:
   

X₃ = t,

Y₃ = m (s – t) – u, (1.14)

Z₃ = 2YZ,

aZ ⁴₃ = 2u (aZ⁴),

де

s = 4XY², u = 8Y⁴, m = 3X² + (a Z⁴), і t = –2s + m². (1.15)
Змішані координати

Представлення точки еліптичної кривої в афінних, проективних координатах, координатах Якобі або модифікованих координатах Якобі має обчислювальні переваги й недоліки. Немає ніякої системи координат, яка забезпечує обидва як швидкі складання, так і швидкі подвоєння. Можливо змішування різних координат, тобто додання двох точок, де перша задається в деякій одній системі координат, а друга – в деякій іншій системі координат. Ми можемо також вибрати систему координат результату. Оскільки ми маємо чотири різні види систем координат, це надає велике число можливостей. Змішані координати надають кращу комбінацію систем координат для подвоєнь або складань для мінімізації часу для піднесення до ступеня еліптичної кривої. Змішані координати діють найефективніше в алгоритмі попереднього обчислення [49].
2.4. Груповий закон для еліптичних кривих E( F(2^m))

Груповий закон в афінних координатах

Нехай F(2^m) для деякого m ≥ 1 є кінцевим полем. Нехай E є еліптичною кривою над F(2^m), що задана рівнянням:

Y² + XY = X³ + aX² + b (1.16)

з a, b ∈ F(2^m) – такими, що b ≠0_F.

В афінних координатах груповий закон на еліптичній кривій (1.16) визначається таким чином:

⎯ точка на нескінченності є одиничним елементом 0_Eщодо «+»;

⎯ якщо R = (x, y) ≠ 0_Eє точкою на E, що задана в афінній системі координат, то –R = (x, x + y);

⎯ для точок R₁ = (x₁, y₁) та R₂ = (x₂, y₂) – таких, що R₁ ≠ ±R₂ і R₁, R₂ ≠ 0_E існує сума у вигляді точки R₃ = (x₃, y₃), де:

x₃ = r² + r + x₁ + x₂ + a;

y₃ = r (x₁ + x₃) + x₃ + y₁, (1.17)

r = (y₂ + y₁) / (x₂ + x₁).

⎯  якщо R = (x, y) є точка на E – така, що R ≠ 0_Eта x ≠ 0,то її подвоєнням є точка 2R = (x₃, y₃), де:

x₃ = r² + r + a;

y₃ = x² + (r + 1_F) x₃, (1.18)

r = x + (y / x).

У разі коли R = (0_F, y), її подвоєнням є 2R = 0_E.

При обчисленні згідно з (1.18) необхідно виконувати операцію ділення за модулем, що вимагає значних потужностей. Складність обчислень може бути пониженою при виконанні групових операцій у проективних координатах.
Груповий закон у проективних координатах для еліптичних кривих Е( F(2^m))

Проективний аналог афінного рівняння (1.16) визначається над П_proj (F(2^m)) і задається однорідним кубічним рівнянням:

Y²Z + XYZ = X³ + aX²Z + bZ³ з a, b ∈ F(2^m). (1.19)

Безліч усіх трійок, еквівалентних (X, Y, Z), позначається як (X, Y, Z)/.

---

Еліптична крива, задана в проективних координатах, складається з усіх точок R = (X, Y, Z) функції F(2^m) × F(2^m) × F(2^m) \ {(0F, 0F, 0F)} – таких, що трійка (X, Y, Z) є рішенням рівняння (1.19).

Коли еліптична крива задається в афінних координатах, а точка R – у проективних координатах, то справедливі твердження:

1) Якщо Q = (x_Q, y_Q) є афінною точкою E, то R = (x_Q, y_Q, 1_F) є відповідною точкою в проективних координатах.

2) Якщо R = (X, Y, Z) (з Z ≠ 0_F) є рішенням (1.19), то Q = (X/Z, Y/Z) є відповідною афінною точкою E.

3) Існує тільки одне рішення (1.19) з Z = 0_F, а саме (0_F, 1_F, 0_F). Ця точка відповідає O_E.

У проективних координатах груповий закон на еліптичній кривій, що задана для (1.19), формулюється таким чином:

1. 
   Точка (0_F, 1_F, 0_F) є одиничним елементом 0_E щодо операції «+».
   
2. 
   Якщо R = (X, Y, Z) ≠ (0_F, 1_F, 0_F) є точкою на E,заданою в проективних координатах, то:
   

R= (X, X+ Y, Z).

Нехай R₁ = (X₁, Y₁, Z₁) та R₂ = (X₂, Y₂, Z₂) є дві точки на E – такі, що R₁ ≠ R₂ і R₁, R₂ ≠ (0_F, 1_F, 0_F), тоді суму цих точок як точку R₃ = (X₃, Y₃, Z₃) можна обчислити за допомогою таких формул:

X₃ = su;

Y₃ = t (u + s²X₁Z₂) + s³Y₁Z₂ + su; (1.20)

Z₃ = s³Z₁Z_3,

де

s = X₂Z₁ + X₁Z₂, t = Y₂Z₁ + Y₁Z₂, і u = (t² + ts + as²) Z₁Z₂ + s³.

Нехай R = (X, Y, Z) ≠ (0_F, 1_F, 0_F) є точка на E, тоді її подвоєння 2R = (X₃, Y₃, Z₃) можуть бути обчислені за допомогою таких формул:

X₃ = st;

Y₃ = X⁴s + t (s + YZ + X²); (1.21)

Z₃ = s³,

де

s = XZ і t = bZ⁴ + X⁴.

2.5 Груповий закон для еліптичних кривих E( F(3^m))

Груповий закон в афінних координатах

Нехай

---

F(3^m) для деякого цілого m ≥ 1 є кінцевим полем. Нехай також E є еліптичною кривою над полем F(3^m), що задана рівнянням:

Y² = X³ + aX² + b, з a, b ∈ F(3^m), (1.22)

причому a, b ≠ 0_F.

В афінних координатах груповий закон на еліптичній кривій, що задана як (1.22), визначається таким чином:

• 
  точка на нескінченності є одиничним елементом 0_Eщодо операції «+»;
  

– якщо R = (x, y) ≠ 0_Eє точкою на E, що задана в афінній системі координат, тоді

R = (x, x + y);

• 
  якщо R₁ = (x₁, y₁) та R₂ = (x₂, y₂) є дві відмінні точки на кривій E – такі, що R₁ ≠ ±R₂ і R₁, R₂ ≠ 0_E,тоді їх сумою є точка R₃ = (x₃, y₃), де:
  

x₃ = r² – a – x₁ – x₂,

y₃ = r (x₁ – x₃) – y₁, (1.23)

причому

r = (y₂ – y₁) / (x₂ – x₁);

⎯ якщо R = (x, y) є точка на кривій E – така, що R ≠ 0_Eта y ≠ 0_F, то її подвоєнням є точка 2R = (x₃, y₃), координати якої визначаються згідно з формулами:

x₃ = r² – a + x,

y₃ = r (x – x₃) – y, (1.24)

причому

r = ax / y (окрім випадків, коли R = (x, 0_F)), то її подвоєнням є 2R = 0_E.
Груповий закон у проективних координатах

Проективний аналог афінного рівняння (1.22) визначається над П_proj (F(3^m)) і задається однорідним кубічним рівнянням:

Y²Z = X³ + aX²Z + bZ³ з a, b ∈ F(3^m). (1.25)

Еліптична крива, задана в проективних координатах, складається з усіх точок R = (X, Y, Z) для F(3^m) × F(3^m) × F(3^m) /{(0_F, 0_F, 0_F)} – таких, що трійка (X, Y, Z) є розв’язком рівняння (1.25).

Якщо еліптична крива задається в афінних координатах, а точка R – у проективних координатах, то справедливі твердження:

⎯  якщо Q = (x_Q, y_Q) є афінною точкою E, то R = (x_Q, y_Q, 1_F) є відповідною точкою в проективних координатах;

⎯ якщо R = (X, Y, Z) (з Z ≠ 0_F) є рішенням (7.10), то Q = (X/Z, Y/Z

---

) є відповідною точкою в афінних координатах;

⎯ існує тільки одне рішення рівняння (1.25) з Z = 0_F, а саме: точка (0_F, 1_F, 0_F), що відповідає 0_E.
У проективних координатах груповий закон на еліптичній кривій, що задана для (1.25), є таким:

⎯ точка (0_F, 1_F, 0_F) є одиничним елементом 0_Eщодо операції «+».

⎯  якщо R = (X, Y, Z) ≠ (0_F, 1_F, 0_F) є точкою на кривій E, що задана в проективних координатах, то й R = (X, X + Y, Z).

⎯ якщо R₁ = (X₁, Y₁, Z₁) та R₂ = (X₂, Y₂, Z₂) є дві відмінні точки на кривій E, але такі, що R₁ ≠ ±R₂ і R₁, R₂ ≠ (0_F, 1_F, 0_F), тоді їх сума R₃ = (X₃, Y₃, Z₃) може бути обчислена за допомогою формул:

X₃ = st²Z₁Z₂ – s³u;

Y₃ = t (sX₁Z₂ – t²Z₁Z₂ + s²u) – s³Y₁Z²; (1.26)

Z₃ = s³Z₁Z_2,

причому

s = X₂Z₁ – X₁Z₂, t = Y₂Z₁ – Y₁Z₂, та u = aZ₁Z₂ + X₁Z₂ + X₂Z₁;

⎯  якщо R = (X, Y, Z) ≠ (0_F, 1_F, 0_F) є точкою на кривій E, тодіїї подвоєння

2R = (X₃, Y₃, Z), тобто координати X₃, Y₃ і Z₃ можуть бути обчислені за допомогою таких формул:

X₃ = tY;

Y₃ = s (XY² – t) – Y⁴; (1.27)

Z₃ = Y³Z,

причому

s = aX і t = s²Z – aY²Z + XY².

Виконання операцій додавання та подвоєння при скалярному множенні вимагає виконання складної операції ділення за модулем над полем F(3^m). Цей недолік деякою мірою усувається при застосуванні проективних базисів.


2.6 Складність обчислень у різних системах координат

Нижче наводяться оцінки складності виконання операцій в різних системах координат [31-32].

У разі коли E(F(q)) з p > 3, існує п’ять систем координат: афінні координати, проективні координати, координати Якобі, модифіковані координати Якобі та змішані координати. У випадках E(F(2^m)) і E (F(3^m

---

)) існує дві системи координат: афінні координати та проективні координати.

Позначимо відповідно афінні координати, проективні координати, координати Якобі й модифіковані координати Якобі символами А, P, J і J_m; час складання точок в координатах C₁і C₂з результатом в координатах C₃ як t (C₁ + C₂ = C₃); час подвоєння точки в координатах C₁ з результатом в координатах C₂ як t (2C₁ = C₂); і множення точок (зворотне та зведення у квадрат) у полі F(q) як М (відповідно I та S). У таблиці 1.1 надаються характеристики системи координат E(F(q))з p > 3. У таблиці 1.2 надаються характеристики системи координат E(F(2^m)). У таблиці 1.3 надаються характеристики системи координат E(F(3^m)).
Таблиця 1.1

Характеристики системи координат E(F(q)) з p > 3

Подвоєння		Складання
Операція	Складність обчислення	Операція	Складність обчислення
t (2P)	7M + 5S	t (Jm + Jm)	13M + 6S
t (2J)	4M + 6S	t (J + J)	12M + 4S
t (2Jm)	4M + 4S	t (P + P)	12M + 2S
t (2Jm = J)	3M + 4S	t (J + A = Jm)	9M + 5S
t (2A = Jm)	3M + 4S	t (Jm + A = Jm)	9M + 5S
t (2A = J)	2M + 4S	t (J + A = J)	8M + 3S
–	–	t (Jm + A = J)	8M + 3S
–	–	t (A + A = Jm)	5M + 4S
t (2A)	2M + 2S + I	t (A + A)	2M + S + I

---

Смотрите также файлы

• Решите задачи, сославшись на текст Салической правды Статья xlvii салической правды.doc

• Строить образы простейших фигур при повороте.docx

• Б. М. Глинский канд техн наук, доцент.pdf

• Инструкция по доступу прилагается к заданию в курсе. Откройте на виртуальном лабораторном столе папку Лабораторные работы.docx

• Программа учебного предмета Основы безопасности жизнедеятельности 24 класс 1 вариант г. Братск.docx