Таблиця 1.2

Характеристики системи координат E(F(2^m))

Подвоєння		Складання
Операція	Складність обчислення	Операція	Складність обчислення
t (2P)	7M + 5S	t (P + P)	16M + 2S
t (2A)	2M + S + I	t (A + A)	2M + I

Таблиця 1.3

Характеристики системи координат E(F(3^m))

Подвоєння		Складання
Операція	Складність обчислення	Операція	Складність обчислення
t (2P)	9M + 3S	t (P + P)	15M + 2S
t (2A)	3M + S + I	t (A + A)	2M + S + I

2.7 . Основні властивості щодо еліптичних кривих
У цьому підрозділі подані відомості щодо еліптичних кривих, які необхідні для асиметричних криптографічних перетворень у групі точок еліптичної кривої.

0

1.4.1. Властивості еліптичних кривих

Порядок еліптичної кривої

Еліптична крива E над полем F(q) має бінарною операцією «+» складання точок E × E → E, для якоїдвом точкам Q₁, Q₂на E може бути обчисленатретя точка Q₁+ Q₂на E. Еліптична крива E є абелевою групою щодо операції «+».

Число точок еліптичної кривої E (включаючи точку нескінченності 0_E) називається порядком E і позначається як #E(F(q)). Порядок кривої #E(F(q)) визначається згідно з теоремою Хасе [ ]:

q +1 – 2√q ≤ #E (F(q)) ≤ q + 1 + 2√q. (1.28)

Ціле число t, визначене як t = q +1 – #E(F(q)),називаєтьсяслідом. Теорема Хасе визначає межу по сліду.
Аномальні та супер сингулярні криві

Еліптична крива

---

E,щовизначена над полем F(q) з порядком #E(F(q))= p^m, де q = p^m,називається аномальною.

Еліптична крива E, визначена над F(q) зі слідом t, кратним p, називається супер сингулярною.

Аномальні криві вразливі до атак з використанням алгоритмів Аракі-Сатока , Смарта і Сімаіва [49].

Відносно супер сингулярних кривих існують вразливості, засновані на алгоритмах Фрея-Рюка та Менезіса-Окамото-Ванстона [47 - 49].
Умови існування еліптичної кривої

Порядок еліптичної кривої, що визначена над полем F(P)

Слід кривої E над полем F(p) згідно з теоремою Хасе обмежений відрізком [–2√p, 2√p]. Також згідно з теоремою Вотерхауза для t в діапазоні [–2√p, 2√p] існує еліптична крива E над F(p) зі слідом t.

Теорема Вотерхауз1. Кожне ціле n в інтервалі, що заданий згідно з теоремою Хасе, є порядком деякої еліптичної кривої, визначеної над F(p).
Порядок еліптичної кривої, що визначена над полем F(P^m)

Слід кривої E над полем F(2^m) згідно теореми Хасе обмежений відрізком [–2√2^m, 2√2^m]. Згідно з теоремою Вотерхауза для t в діапазоні [–2√2^m, 2√2^m] існує еліптична крива E над F(2^m) із слідом t.

Теорема1.1 Вотерхауза . Нехай t є цілим числом, де | t | ≤ 2√2^m, тоді існує еліптична крива, що визначена над полем F(2^m), порядку 2^m + 1 – t, якщо, і тільки якщо, виконується одна з таких умов:

• 
  t непарне;
  
• 
  t = 0; (1.29)
  
• 
  m непарне і t² = 2^m+1;
  
• 
  m парне і t² = 2^m+2 або t² = 2^m.
  

Порядок еліптичної кривої, що визначена над полем F(3^m)

Слід E над полем F(p^m) згідно з теоремою Хасе обмежений відрізком [–2√3^m, 2√3^m]. Згідно з теоремою Вотерхауза для t вдіапазоні [–2√3^m, 2√3^m] існує еліптична крива E над F(3^m) зі слідом t.

Теорема 1.2 Вотерхауз1. Нехай t є ціле, де | t | ≤ 2√3^m. Тоді існує еліптична крива, визначена над F(3^m) порядку 3^m+1 – t, якщо, і тільки якщо, дотримується одна з таких умов:

• 
  t єне кратне 3;
  

m є непарне і дотримується одне з наступного:

• 
  t = 0;
  
• 
  t² = 3^m+1 та p = 3. (1.30)
  

m є парне і виконується одна з умов:

---

• 
  t² = 4 3^m;
  
• 
  t² = 3^m 3;
  
• 
  t = 0.
  

Нехай E є еліптичною кривою над F(q), де q = p^m, і нехай n буде відносно простим числом для характеристики p функції F(q). Група n-кручення генерується двома точками, коли n – відносно просте число до p. E(F(q)) включає точку n-кручення G₁, оскільки #E (F(q)) кратне простому n. Відзначимо, що цей факт не має на увазі E(F(q)) ⊃ E[n].
Додаток А Приклади розв’язку задач та задачі для самостійного розв’язання
1.9.1 Прикладирозв’язку задач
Задача 1.

Скласти точки P1 і P2. P1=(12, 19), P2=(5, 4). Якщо еліптична крива має вигляд , тобто a = 1, b = 1, P = 23.
Розв’язок задачі:

.

Знаходимо в полі G(23) обернений елемент Z, розв’язавши порівняння

7*Z1 (mod 23).

Це порівняння має розв’язок при Z = 10, тому

 = 15*10 (mod 23) = 12.

= 12² – 12 –5 = 144 - 12 – 5 (mod23) = 127 mod23 = 12 mod23.

=12*(12 - 12) - 19(mod23) = 4mod23.

Таким чином:

P₁ + P₂ = (x₁, y₁) + (x₂, y₂) = P₃ = (x₃, y₃) = (12, 4).

P₃=(12,4).
Задача 2.

Знайти точку, яка дорівнює . . Еліптична крива має вигляд

, тобто a=1, b=1.
Розв’язок задачі:

Спочатку подвоїмо точку , тобто знайдемо .

Знайдемо , використовуючи (1.88)

.

Знайдемо зворотний елемент

;

---

.

Значить .

Використовуючи (1.85)-(1.86) та враховуючи, що х₁=х₂, знайдемо координати х₂ і у₂ точки P₂(x₂,y₂)

;

.

Таким чином: .
Далі знайдемо суму точок P₁+P₂=P₁+2P₁=P₃=(x₃, y₃).

.

Знайдемо , використовуючи (1.87)

.

Знайдемо зворотний елемент

; .

Значить .

Використовуючи (1.85) і (1.86), знайдемо х₃ та у₃

;

.

Таким чином: 3Р₁ =3(5, 4) = (13, 16).

---

Задача 3.

Нехай є ЕК з рівнянням: , a=1, b=1, p=23.

Перевірити, чи належать такі точки ЕК:

(1, 7), (1, 16).
Розв’язок задачі:

, точка (1,7) не належить ЕК;

, точка (1,16) належить ЕК.
Задача 5.

Побудувати , m=4, , .
Розв’язок задачі:

Поле – може бути задано 16 поліномами не вище третього
ступеня, наприклад, поліномами над полем GF (2).



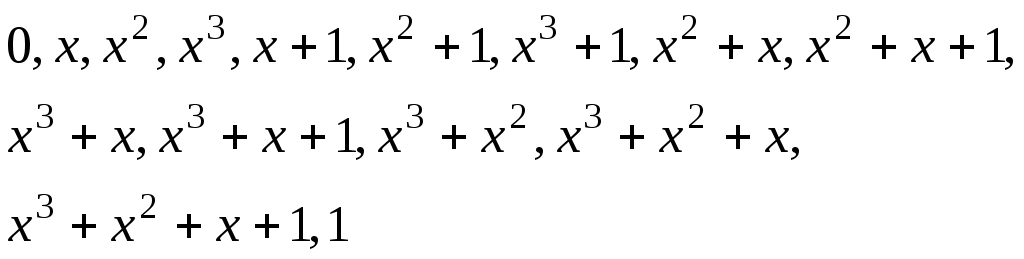
Елементи поля можуть бути задані в двійковому вигляді, тоді, наприклад,

x³+ x²+11101

x³+11001.

Операція множення елементів поля виконується в полі GF(P).

Наприклад:



Зведемо цей поліном за модулем f(x) = x⁴+ x+1. У результаті маємо:



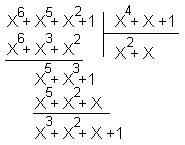
Таким чином: (x³+ x²+1)(x³+ 1)(mod (x⁴+ x+1),2) = x³+ x²+x +11111.

В табл. 1.5 наведені елементи a^jдляj= , якщо = x.
Таблиця 1.5 – Значення a^j

j	0	1	2	3	4	5	6	7
 j	1	x	x2	x3	x+1	x2+x	x3+x2	x3+x2+x+1

---

Смотрите также файлы

• Решите задачи, сославшись на текст Салической правды Статья xlvii салической правды.doc

• Строить образы простейших фигур при повороте.docx

• Б. М. Глинский канд техн наук, доцент.pdf

• Инструкция по доступу прилагается к заданию в курсе. Откройте на виртуальном лабораторном столе папку Лабораторные работы.docx

• Программа учебного предмета Основы безопасности жизнедеятельности 24 класс 1 вариант г. Братск.docx