Елементи поля можна отримати як a^j = ^j (mod f(x),2), j= .
Задача 6.

Нехай задано поле , m=4, , .

Знайти 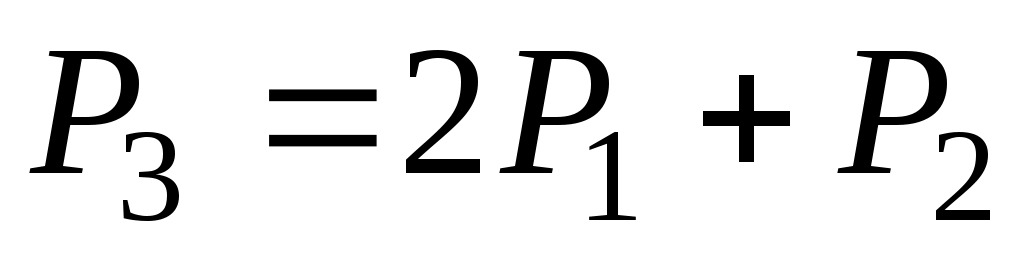, якщо .

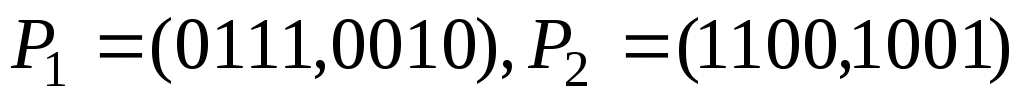Розв’язок задачі:

Знайдемо :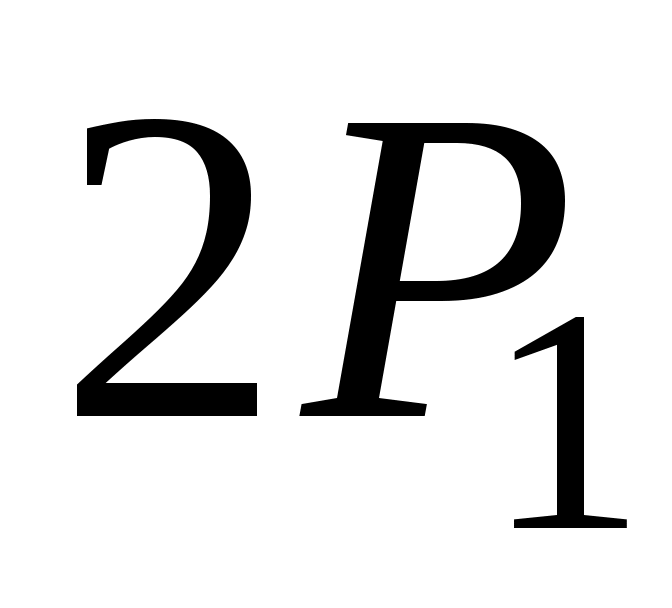

.

Далі знайдемо зворотний елемент для числа 0111, яке подамо поліномом х²+х+1.

Враховуючи, що:

;

.

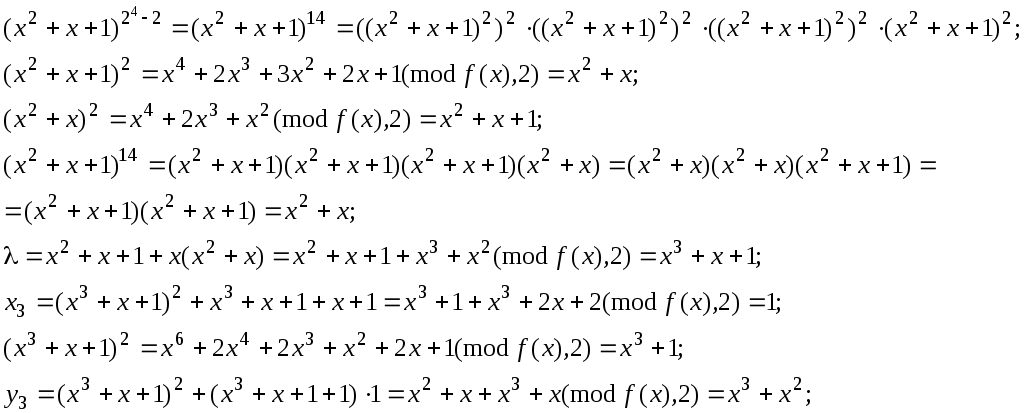
Знайдемо :



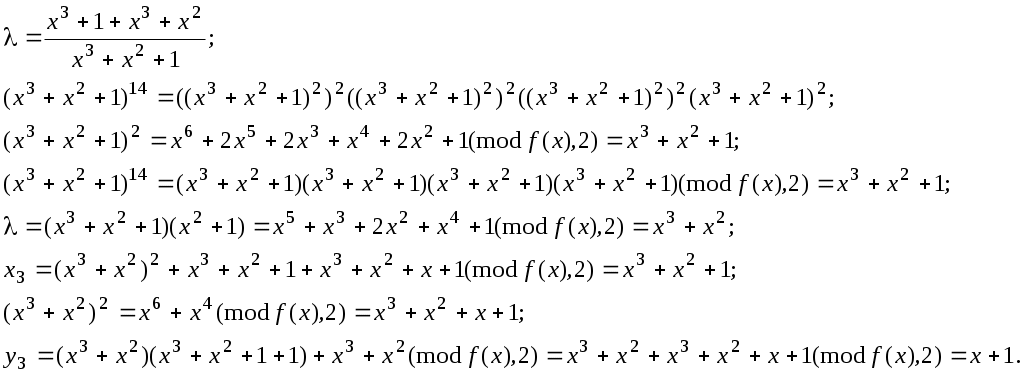
Таким чином:

.
Додаток В Задачі для самостійного розв’язання
1. Нехай є ЕК з рівнянням: , a=1, b=1, p=23.

Перевірити, чи належать точки, що наведені в табл. 1.6, еліптичній кривій:

Таблиця 1.6 – Значення

N	1	2	3	4	5	6	7	8	9	10	11	12
	(3,10)	(3,13)	(4,0)	(5,4)	(5,19)	(6,4)	(6,19)	(7,11)	(7,2)	(9,7)	(9,16)	(17,3)
N	13	14	15	16
	(17,20)	(18,20)	(19,5)	(13,16)

---

Якщо n= k (mod 17), k – номер в журналі.

Якщо k=17, то k=k+1.

2. Знайти ( з попередньої задачі).

3. Знайти , якщо ( з попередньої задачі).

4. Знайти і , якщо , а еліптична крива має вигляд ,

	1	2	3	4	5	6	7	8

---

k – номер за списком, якщо k=8, то .

---

Смотрите также файлы

• Решите задачи, сославшись на текст Салической правды Статья xlvii салической правды.doc

• Строить образы простейших фигур при повороте.docx

• Б. М. Глинский канд техн наук, доцент.pdf

• Инструкция по доступу прилагается к заданию в курсе. Откройте на виртуальном лабораторном столе папку Лабораторные работы.docx

• Программа учебного предмета Основы безопасности жизнедеятельности 24 класс 1 вариант г. Братск.docx