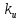Добавлен: 23.11.2023
Просмотров: 54
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство науки и высшего образования Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Институт математики и информационных технологий
Кафедра программного обеспечения вычислительной техники и
автоматизированных систем
Отчёт
по расчётно-графической работе
по дисциплине «Основы теории управления»
Компьютерное моделирование систем управления
ОГУ 09.03.01.4023.837 О
| Руководитель кандидат техн. наук, профессор А.М. Семенов «»2023 г. Студент группы название А.В. Лаптиев «»2023 г. |
Оренбург 2023
«УТВЕРЖДАЮ»
-
Заведующий кафедрой
Д.В. Горбачев
«__» ________ 2023 г.
ЗАДАНИЕ
НА РГЗ
Исполнитель Лаптиев Артур Витальевич
Группа 20ИВТ(б)ПОВТ
Руководитель Семенов Анатолий Михайлович
Тема: «Компьютерное моделирование систем управления».
Цель работы:
1. Освоить отдельные понятия и вопросы теории управления (регуляторы, корректирующие элементы, структурно-неустойчивые системы, жесткие и гибкие обратные связи в качестве корректирующих элементов, введение в закон регулирования производных и интегралов, применение астатических звеньев в качестве корректирующих элементов; оптимальный переходный процесс; критерий оптимальности; интегральные методы оценки качества систем).
2. Закрепить навыки работы с ПК «МВТУ»; методику определения устойчивости систем управления (СУ) с помощью временных характеристик;
3. Получить практические навыки программной реализации алгоритмов управления.
Исходные данные для работы (согласно варианту 22):
1) структурная схема исходной системы управления:

2)
исходные параметры:
- нулевые начальные условия;
- ступенчатое входное воздействие U(t) = 0.8(t);
- коэффициент усиления усилителя K1 = 1;
- коэффициент усиления 1-го апериодического звена K2 = 10;
- постоянная времени 1-го апериодического звена Т2 = 2.5 сек.;
- коэффициент усиления 2-го апериодического звена K3 = 3;
- постоянная времени 2-го апериодического звена Т3 = 4 сек.;
3) требования к системе управления:
- ПД закон регулирования;
- заданное значение отклонения регулируемой величины Yне более 5 %, т. е. = ±5 · 0.05 = ±0.25 (при определении tр);
- варьируемые параметры: параметры корректирующего устройства;
- нулевая ошибка ε(t);
- время регулирования tр не более 10 сек.;
- перерегулирование σ не более 30%.
Материалы, представляемые к защите:
-
расчетно-пояснительная записка, набранная и распечатанная в текстовом редакторе Microsoft Word; -
интерфейс программы; -
листинг.
Дата выдачи задания: «__» ______2023 г.
Руководитель_______________
(подпись)
Срок сдачи законченной работы: «__» ______2023 г.
Задание принял к исполнению: «__» ______ 2023 г.
_______________
(подпись)
Цель работы: исследование и программная реализация типовых алгоритмов управления.
Задачи работы: получить практические навыки в построении цифровых моделей систем управления.
1 Общие сведения
1.1 Основные понятия синтеза СУ
Синтез САУ – процедура определения структуры и параметров системы по заданным показателям качества управления. Как любая обратная задача, задача синтеза в отличие от задачи анализа имеет множество решений для одних и тех же заданных условий.
Все математические задачи, решаемые в теории управления, можно объединить в два больших класса: задачи анализа; задачи синтеза [1].
Задачи синтеза можно рассматривать как обратные задачам анализа: в них требуется выбрать принцип управления, определить структуру и рассчитать параметры системы по заданным показателям качества управления. Простейшими задачами синтеза являются, например, задачи определения передаточного коэффициента разомкнутой САУ по заданной ошибке или условию минимума интегральной оценки.
Синтез является важнейшим этапом проектирования систем, основным и наиболее важным приложением результатов, полученных теорией автоматического управления, которая сегодня позволяет создать систему управления практически для любого объекта. Однако спроектировать высококачественную систему управления этим объектом можно лишь при наличии достаточно точной математической модели. Причем, согласно принципу Эшби, сложность управляющего устройства должна быть не ниже сложности объекта управления.
Цели синтеза системы управления [2]:
- создание новой системы управления на основе новых достижения науки и техники;
-совершенствование существующей системы управления на основе выявленных недостатков, а также появления новых задач и требований.
В общем виде задачи синтеза систем управления заключаются в определении структуры и параметров системы исходя из заданных требований к значениям показателей эффективности ее функционирования, а также способов обеспечения целей функционирования системы [4].
Простейшими задачами синтеза являются, например, задачи определения передаточного коэффициента разомкнутой СУ по заданной ошибке или условию минимума интегральной оценки.
Синтез представляет собой многошаговый итеративный процесс, включающий последовательное решение следующих основных задач [9]:
-формирование замысла и цели создания системы управления;
-формирование вариантов новой системы;
-приведение описаний вариантов системы во взаимное соответствие;
-оценка эффективности вариантов и принятия решения о выборе варианта новой системы;
-разработка требований к системе управления;
-разработка программ реализации требований к системе управления;
-реализация разработанных требований к системе управления.
В общем случае при проектировании системы необходимо определить алгоритмическую и функциональную структуры системы, т. е. решить задачу полного синтеза. Определение алгоритмической структуры (теоретический синтез) производится с помощью математических методов и на основании требований, записанных в четкой математической форме.[9]
Определение функциональной структуры (технический синтез) заключается в выборе конкретных физических элементов и согласования их между собой по статическим и энергетическим характеристикам. Эта процедура не имеет пока строгой математической основы (т. е. не формализована) и поэтому относится к области инженерного творчества.
Так как не всякий элемент полученной в результате расчета алгоритмической структуры может иметь отображение в виде физического блока функциональной структуры (не может быть физически реализован), задачу синтеза в большинстве случаев невозможно решить, определяя сначала алгоритмическую структуру САУ, а затем по ней – функциональную структуру. Поэтому задачу синтеза в большинстве случаев решают следующим образом.
Cначала, исходя из известности объекта управления ОУ, требований к назначению и условиям работы СУ, по каталогам серийного оборудования выбирают функционально необходимые элементы системы: регулирующий орган РО; исполнительное устройство ИУ; датчики Д.
Эти элементы СУ вместе с объектом управления ОУ представляют неизменяемую часть функциональной структуры системы (рисунок 1).
Затем, на основании требований к статическим и динамическим свойствам СУ определяют изменяемую часть функциональной структуры системы, в которую входят: усилительно-преобразующий блок УПБ; корректирующие устройства КУ[12].
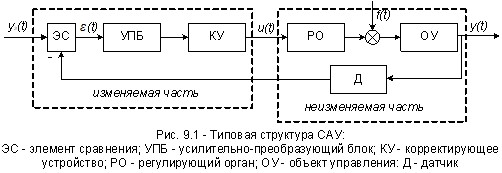
Рисунок 1 – Функциональная структура системы
Таким образом, процедуры определения алгоритмической и функциональной структур тесно переплетаются друг с другом. Окончательное решение о структуре СУ принимается на основе компромисса между качеством управления, с одной стороны, и простотой и надежностью, с другой. Заключительным этапом проектирования СУ является параметрическая оптимизация - определение настроечных параметров выбранного регулятора. После решения задачи синтеза обычно выполняют анализ синтезированной системы, т. е. проверяют, обладает ли система необходимыми показателями устойчивости и качества управления. Применение на всех этапах синтеза и анализа СУ цифровых вычислительных машин позволяет рассмотреть большое количество вариантов структур и параметров и тем самым существенно ускорить решение задачи синтеза [16].
1.2 Общие принципы синтеза алгоритмической структуры СУ
Для решения задачи синтеза, например, алгоритмической структуры типовой одноконтурной СУ должны быть известны:
-
передаточная функция объекта управления Wо(p); -
возмущение, действующее на выходе объекта f(p) рисунок 2.
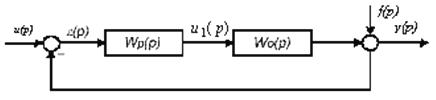
Рисунок 2 – Алгоритмическая структура типовой одноконтурной СУ
Результатом решения задачи синтеза алгоритмической структуры должна быть передаточная функция регулятора
 .
.Пропорциональный алгоритм регулирования (П-алгоритм)
Зачастую при создании СУ на первом этапе проектирования в алгоритм ее функционирования закладывают простейший закон регулирования, согласно которому связь между сигналом рассогласования
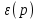 и сигналом
и сигналом 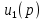 следующая:
следующая: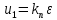 , (1)
, (1)где
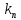 – передаточный коэффициент.
– передаточный коэффициент.Такой закон регулирования называют пропорциональным (П-закон регулирования). Ему соответствует передаточная функция:
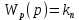 . (2)
. (2)Это простейший алгоритм, который реализуется при помощи безинерционного звена. Преимущества П-регулятора – простота и быстродействие. Недостатки – ограниченная точность (особенно при управлении объектами с большой инерционностью и запаздыванием).
Интегральный алгоритм регулирования (И-алгоритм)
Этот алгоритм реализуется при помощи интегрального звена с передаточной функцией:
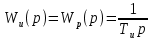 , (3)
, (3)где
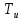 – постоянная времени,
– постоянная времени, 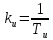 – коэффициент передачи звена.
– коэффициент передачи звена.Тогда в закон регулирования вводят интеграл от сигнала рассогласования:
 . (4)
. (4)При интегральном алгоритме регулирования управляющее воздействие
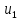 в каждый момент времени пропорционально интегралу от сигнала ошибки. Преимущества И-регулятора - лучшая (по сравнению с П-регулятором) точность в установившихся режимах, недостатки - худшие свойства в переходных режимах (меньшее быстродействие и более высокая колебательность).
в каждый момент времени пропорционально интегралу от сигнала ошибки. Преимущества И-регулятора - лучшая (по сравнению с П-регулятором) точность в установившихся режимах, недостатки - худшие свойства в переходных режимах (меньшее быстродействие и более высокая колебательность).Пропорционально-интегральный алгоритм регулирования (ПИ-алгоритм)
Этот алгоритм реализуется при помощи регулятора с передаточной функцией:
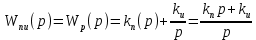 , (5)
, (5)где
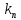 ,
,