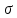Добавлен: 23.11.2023
Просмотров: 56
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– передаточные коэффициенты.
В этом случае закон регулирования, называемый пропорционально-интегральным (ПИ-законом регулирования), будет описываться следующим уравнением:
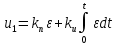. (6)
Введение интеграла в закон регулирования исключает статическую ошибку СУ, превращая ее в астатическую систему, но при этом одновременно уменьшаются запас устойчивости и быстродействие системы.
Благодаря наличию интегральной составляющей в алгоритме, ПИ-регулятор обеспечивает высокую точность в установившихся режимах, а при определенном соотношении коэффициентов
,
обеспечивает хорошие показатели и в переходных режимах. Поэтому он получил наибольшее распространение в промышленной автоматике.
Пропорционально-дифференциальный алгоритм регулирования (ПД-алгоритм)
Этот алгоритм реализуется при помощи пропорционального регулятора и введением в закон регулирования производной от сигнала рассогласования. Передаточная функция алгоритма:
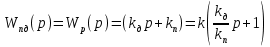, (7)
где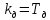
– коэффициент дифференцирующего звена.
Закон регулирования имеет вид:
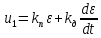. (8)
Регулятор, реализующий ПД-закон регулирования, реагирует не только на значение отклонения регулируемой величины в данный момент времени, но и на скорость изменения отклонения. Следовательно, регулятор работает с опережением, улучшая качество переходного процесса за счет учета тенденции последующего его развития, т. е. увеличивает быстродействие системы и запас устойчивости. Недостатком пропорционально – дифференциального закона регулирования является ограниченная точность. [6-10].
Пропорционально-интегрально-дифференциальный алгоритм регулирования (ПИД-алгоритм)
Этот алгоритм реализуется при помощи регулятора с передаточной функцией:
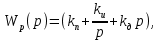(9)
где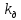
, , – постоянные коэффициенты.
ПИД-закон регулирования, реализует алгоритм:
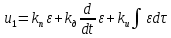. (10)
Совместное введение производной и интеграла обеспечивает желаемое быстродействие, необходимый запас устойчивости и отсутствие статической ошибки СУ. ПИД-алгоритм – наиболее гибкий алгоритм регулирования (в классе линейных алгоритмов). Он сочетает в себе преимущества более простых выше рассмотренных алгоритмов Коэффициенты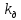 , , входящие в передаточные функции типовых регуляторов, подлежат настройке при наладке СУ и поэтому называются настроечными параметрами. Они имеют наименования: – коэффициенты пропорциональной, интегральной и дифференциальной частей СУ.
2 Моделирование СУ на ЭВМ
Моделирование СУ на ЭВМ базируется на цифровых моделях типовых динамических звеньев (ТДЗ). Основу цифрового моделирования представляет преобразование дифференциального уравнения (ДУ) в разностное. Одним из самых распространенных методов решения дифференциального уравнения является метод Эйлера.
2.1 Сущность метода Эйлера
ДУ представляется в форме Коши:
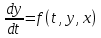, (11)
где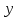
– искомая функция; 
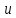– задающее воздействие; 
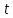– независимая переменная (время).
Сущность метода заключается в том, что если известно значение функции в какой-то (k-1)-й момент, то пользуясь рекуррентным соотношением, можно рассчитать значение функции в k-й момент (рисунок 5).
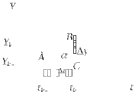
Рисунок 5 – Графическая интерпретация метода
Как видно из рисунка 5:
(12)
Из (12) следует, что для нахождения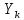
при известном 
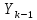, необходимо определить 
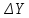. Как следует из решения треугольника АВС:
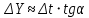, (13)
где
– шаг решения;
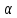– угол наклона касательной к графику 
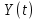в точке 
.
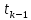Из определения производной следует, что производная – это тангенс угла наклона касательной к графику функции:
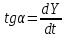. (14)
Как следует из (13,14) можно записать:
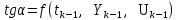. (15)
Подставив (15) в (13) получим:
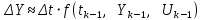. (16)
Тогда уравнение Эйлера для решения ДУ в общем виде запишется следующим образом:
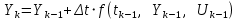. (17)
В таблице 2 приведены цифровые модели (ЦМ) ТДЗ.
Таблица 2 – Цифровые модели ТДЗ
2.2 Компьютерная методика моделирования СУ
Цифровое моделирование включает в себя следующие этапы:
1. Определение ЦМ элементов, входящих в состав СУ.
2. Составление блок-схемы алгоритма ЦМ СУ.
3. Написание программы.
4. Отладка программы.
5. Исследование системы по ЦМ.
Согласно изложенной методике моделирования, используя таблицу 2, определим ЦМ элементов, входящих в систему:
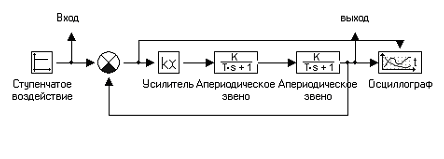
Рисунок 6 – схема объекта управления
Таблица 3 – Цифровые модели ТДЗ входящие в схему
Таблица 3 – Продолжение
Эти элементы являются объектом управления, добавим к нему ПИ регулятор. Рисунок 6
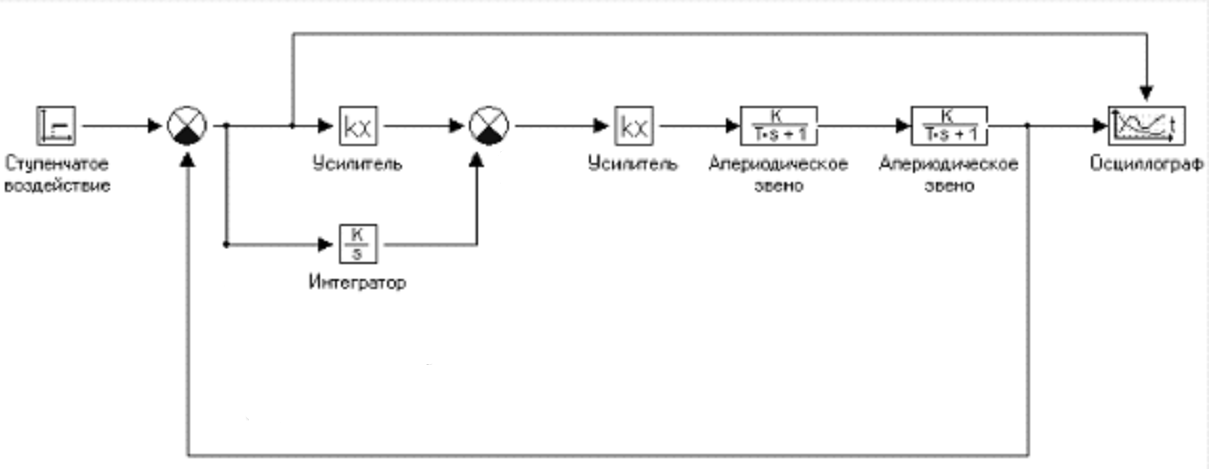
Рисунок 6 - Схема СУ с ПИ регулятором.
; 
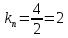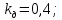
Блок-схема алгоритма цифрового моделирования СУ представлена на рисунке 7.
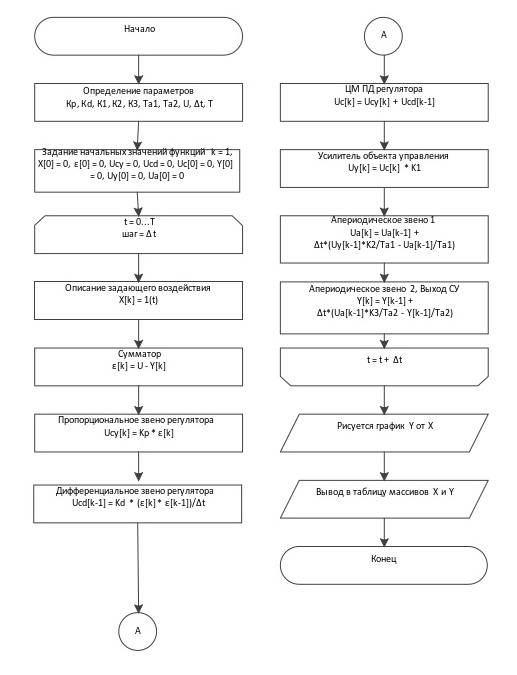
Рисунок 7 - Блок-схема алгоритма цифрового моделирования СУ с ПД регулятором
На рисунке 8 представлен интерфейс программы, позволяющий анализировать влияние параметров СУ на качество процесса управления с параметрами, заданными по варианту и подобранными значениями регулятора.
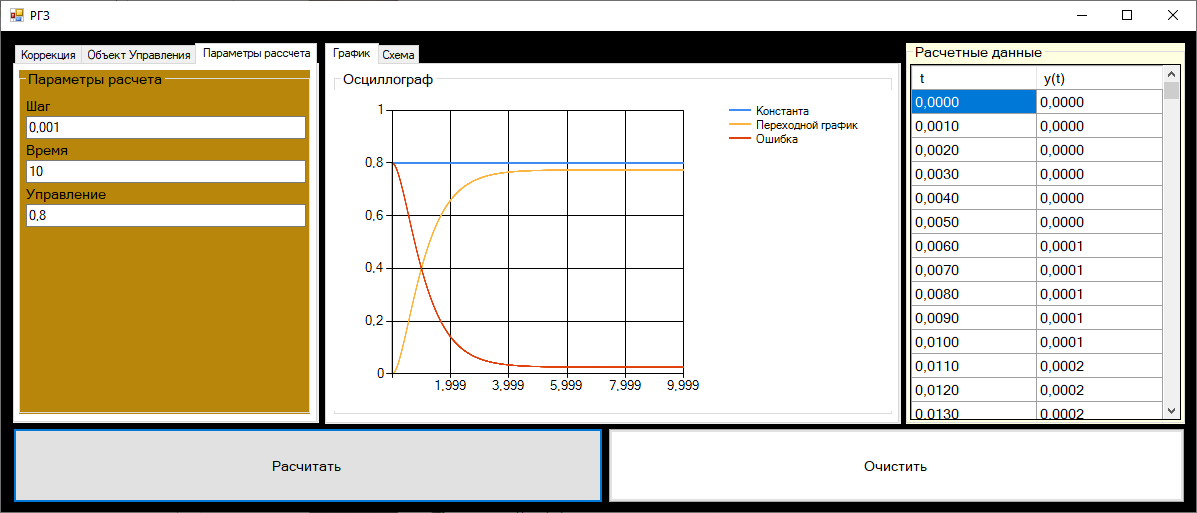
Рисунок 8-интерфейс программы анализа СУ.
На рисунке 9 представлен график, полученный в программном комплексе “МВТУ” с исходными параметрами и параметрами управления, в точности соответствующими установленным в программном средстве. Из графика можно сделать вывод, что результаты программного средства полностью соответствуют результатам “ПК МВТУ”. Время регулирования составляет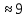
секунд, что соответствует допустимому результату по варианту.
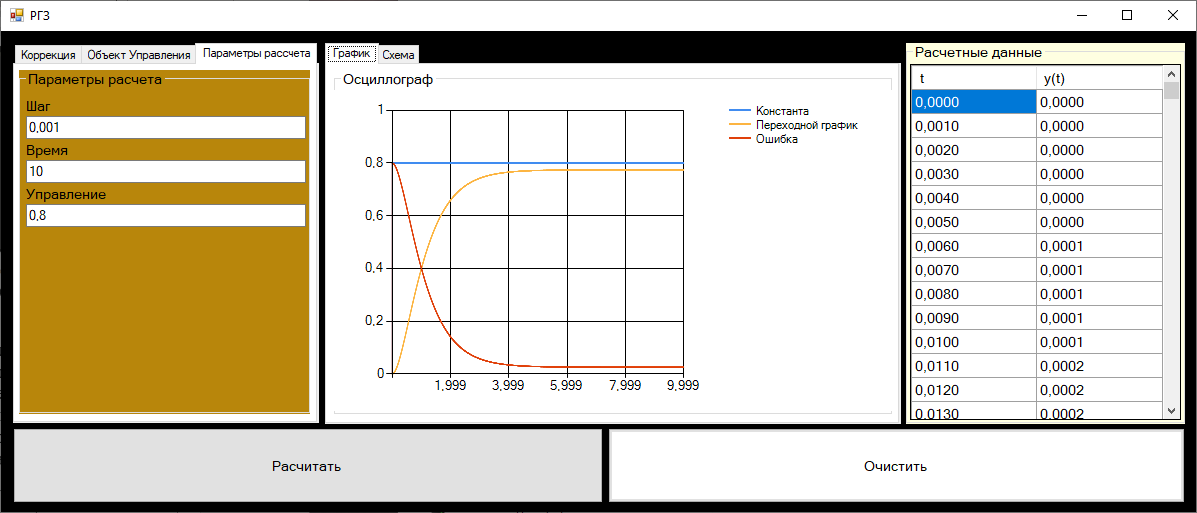
Рисунок 9 – график “ПК МВТУ”
Вывод
В ходе выполнения расчётно-графического задания были освоены отдельные понятия и вопросы теории управления (регуляторы, корректирующие элементы, структурно-неустойчивые системы, жесткие и гибкие обратные связи в качестве корректирующих элементов, введение в закон регулирования производных и интегралов, применение астатических звеньев в качестве корректирующих элементов; оптимальный переходный процесс; критерий оптимальности; интегральные методы оценки качества систем).
Получены практические навыки программной реализации алгоритмов управления в том числе навыки работы с регуляторами.
В ходе экспериментальных исследований можно сформулировать следующие выводы влияния настроечных параметров на показатели качества регулирования:
1.Увеличение коэффициента пропорциональной части регулятора приводит к увеличению перерегулирования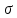
В этом случае закон регулирования, называемый пропорционально-интегральным (ПИ-законом регулирования), будет описываться следующим уравнением:
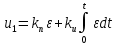. (6)Введение интеграла в закон регулирования исключает статическую ошибку СУ, превращая ее в астатическую систему, но при этом одновременно уменьшаются запас устойчивости и быстродействие системы.
Благодаря наличию интегральной составляющей в алгоритме, ПИ-регулятор обеспечивает высокую точность в установившихся режимах, а при определенном соотношении коэффициентов
, обеспечивает хорошие показатели и в переходных режимах. Поэтому он получил наибольшее распространение в промышленной автоматике.Пропорционально-дифференциальный алгоритм регулирования (ПД-алгоритм)
Этот алгоритм реализуется при помощи пропорционального регулятора и введением в закон регулирования производной от сигнала рассогласования. Передаточная функция алгоритма:
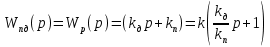, (7)где
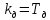– коэффициент дифференцирующего звена.Закон регулирования имеет вид:
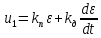. (8)Регулятор, реализующий ПД-закон регулирования, реагирует не только на значение отклонения регулируемой величины в данный момент времени, но и на скорость изменения отклонения. Следовательно, регулятор работает с опережением, улучшая качество переходного процесса за счет учета тенденции последующего его развития, т. е. увеличивает быстродействие системы и запас устойчивости. Недостатком пропорционально – дифференциального закона регулирования является ограниченная точность. [6-10].
Пропорционально-интегрально-дифференциальный алгоритм регулирования (ПИД-алгоритм)
Этот алгоритм реализуется при помощи регулятора с передаточной функцией:
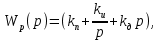(9)где
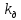, , – постоянные коэффициенты.ПИД-закон регулирования, реализует алгоритм:
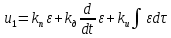. (10)Совместное введение производной и интеграла обеспечивает желаемое быстродействие, необходимый запас устойчивости и отсутствие статической ошибки СУ. ПИД-алгоритм – наиболее гибкий алгоритм регулирования (в классе линейных алгоритмов). Он сочетает в себе преимущества более простых выше рассмотренных алгоритмов Коэффициенты
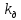, , входящие в передаточные функции типовых регуляторов, подлежат настройке при наладке СУ и поэтому называются настроечными параметрами. Они имеют наименования: – коэффициенты пропорциональной, интегральной и дифференциальной частей СУ.2 Моделирование СУ на ЭВМ
Моделирование СУ на ЭВМ базируется на цифровых моделях типовых динамических звеньев (ТДЗ). Основу цифрового моделирования представляет преобразование дифференциального уравнения (ДУ) в разностное. Одним из самых распространенных методов решения дифференциального уравнения является метод Эйлера.
2.1 Сущность метода Эйлера
ДУ представляется в форме Коши:
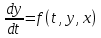, (11)где
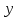– искомая функция; 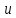– задающее воздействие; 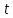– независимая переменная (время). Сущность метода заключается в том, что если известно значение функции в какой-то (k-1)-й момент, то пользуясь рекуррентным соотношением, можно рассчитать значение функции в k-й момент (рисунок 5).
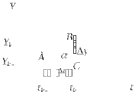
Рисунок 5 – Графическая интерпретация метода
Как видно из рисунка 5:
(12)Из (12) следует, что для нахождения
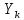при известном 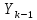, необходимо определить 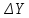. Как следует из решения треугольника АВС: 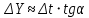, (13)где
– шаг решения; 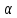– угол наклона касательной к графику 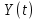в точке 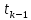.Из определения производной следует, что производная – это тангенс угла наклона касательной к графику функции:
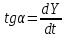. (14)Как следует из (13,14) можно записать:
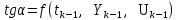. (15)Подставив (15) в (13) получим:
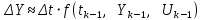. (16)Тогда уравнение Эйлера для решения ДУ в общем виде запишется следующим образом:
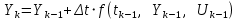. (17)В таблице 2 приведены цифровые модели (ЦМ) ТДЗ.
Таблица 2 – Цифровые модели ТДЗ
| Операторный коэффициент передачи звена | Дифференциальное уравнение | Цифровая модель | ||
| Дифференцирующее звено  - |  |  | ||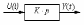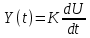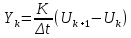
| Интегрирующее звено  |  |  | ||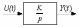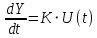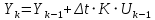
| Апериодическое звено  |  |  | ||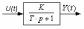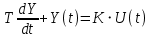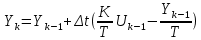
| Форсирующее звено  |  |  | ||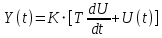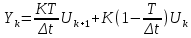
| Колебательное звено  |  |   | ||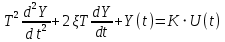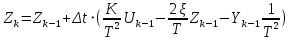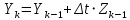
2.2 Компьютерная методика моделирования СУ
Цифровое моделирование включает в себя следующие этапы:
1. Определение ЦМ элементов, входящих в состав СУ.
2. Составление блок-схемы алгоритма ЦМ СУ.
3. Написание программы.
4. Отладка программы.
5. Исследование системы по ЦМ.
Согласно изложенной методике моделирования, используя таблицу 2, определим ЦМ элементов, входящих в систему:
Рисунок 6 – схема объекта управления
Таблица 3 – Цифровые модели ТДЗ входящие в схему
| Элемент | ЦМ |
 |  |
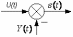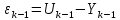Таблица 3 – Продолжение
 |  |
 |  |
| | |
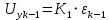Эти элементы являются объектом управления, добавим к нему ПИ регулятор. Рисунок 6
Рисунок 6 - Схема СУ с ПИ регулятором.
| Контроллер | |  |  |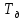
| П |  | – | – |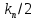
| ПИ |  |  | – |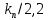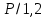
| ПИД |  |  |  |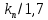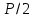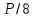
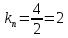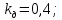
; Блок-схема алгоритма цифрового моделирования СУ представлена на рисунке 7.
Рисунок 7 - Блок-схема алгоритма цифрового моделирования СУ с ПД регулятором
На рисунке 8 представлен интерфейс программы, позволяющий анализировать влияние параметров СУ на качество процесса управления с параметрами, заданными по варианту и подобранными значениями регулятора.
Рисунок 8-интерфейс программы анализа СУ.
На рисунке 9 представлен график, полученный в программном комплексе “МВТУ” с исходными параметрами и параметрами управления, в точности соответствующими установленным в программном средстве. Из графика можно сделать вывод, что результаты программного средства полностью соответствуют результатам “ПК МВТУ”. Время регулирования составляет
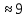секунд, что соответствует допустимому результату по варианту. Рисунок 9 – график “ПК МВТУ”
Вывод
В ходе выполнения расчётно-графического задания были освоены отдельные понятия и вопросы теории управления (регуляторы, корректирующие элементы, структурно-неустойчивые системы, жесткие и гибкие обратные связи в качестве корректирующих элементов, введение в закон регулирования производных и интегралов, применение астатических звеньев в качестве корректирующих элементов; оптимальный переходный процесс; критерий оптимальности; интегральные методы оценки качества систем).
Получены практические навыки программной реализации алгоритмов управления в том числе навыки работы с регуляторами.
В ходе экспериментальных исследований можно сформулировать следующие выводы влияния настроечных параметров на показатели качества регулирования:
1.Увеличение коэффициента
пропорциональной части регулятора приводит к увеличению перерегулирования