Добавлен: 23.11.2023
Просмотров: 55
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, времени 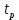 переходного процесса и уменьшению степени затухания.
переходного процесса и уменьшению степени затухания.
2.Увеличение коэффициента дифференциальной части регулятора приводит к уменьшению времени
дифференциальной части регулятора приводит к уменьшению времени 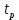 переходного процесса и уменьшению перерегулирования.
переходного процесса и уменьшению перерегулирования.
В пропорционально-дифференцируемом алгоритме регулирования (ПД-алгоритм), регулятор работает с опережением, улучшая качество переходного процесса за счет учета тенденции последующего его развития, т. е. увеличивает быстродействие системы и запас устойчивости. Недостатком пропорционально – дифференциального закона регулирования является ограниченная точность.
Список использованных источников
Приложение А
(обязательное)
Код программы
try
{
{
double kp = Convert.ToDouble(KP.Text),
kd = Convert.ToDouble(KD.Text),
k1 = Convert.ToDouble(K1.Text),
k2 = Convert.To Double(K2.Text),
k3 = Convert.ToDouble(K3.Text),
t1 = Convert.ToDouble(T1.Text),
t2 = Convert.ToDouble(T2.Text),
step = Convert.ToDouble(Step.Text),
u = Convert.ToDouble(U.Text),
out_step = 0.01;
int st = 1,
time = Convert.ToInt32(Convert.ToDouble(Time.Text) / Convert.ToDouble(Step.Text));
List x = new List() { 0 };
List un = new List() { 0 };
double
cd_prev = 0,
cd_next = 0;
List uc = new List() { 0 };
List uy = new List() { 0 };
List ua1 = new List() { 0 };
List ua2 = new List() { 0 };
List y = new List() { 0 };
List err = new List() { 0 };
int k = 1;
for (int t = 0 + st; t <= time; t += st)
{
x.Add(t * step);
un.Add(u);
err.Add(un[k] - y[k - 1]);
if (k > 1)
cd_next = -(y[k - 1] - y[k - 2]) / step;
else
cd_next = -y[k - 1] / step;
uc.Add(err[k] * kp +
cd_prev * kd
);
uy.Add(uc[k] * k1);
ua1.Add(ua1[k - 1] + step * (k2 / t1 * uy[k] - ua1[k - 1] / t1));
ua2.Add(ua2[k - 1] + step * (k3 / t2 * ua1[k] - ua2[k - 1] / t2));
y.Add(ua2[k]);
k++;
cd_prev = cd_next;
}
chart_graph("Константа", x, un, SeriesChartType.Line);
chart_graph("Переходной график", x, y, SeriesChartType.Line);
chart_graph("Ошибка", x, err, SeriesChartType.Line);
int tab_step = 1;
if (st < out_step)
tab_step = Convert.ToInt32(st / out_step);
Tab.RowCount = time / tab_step + 1;
for (int i = 0; i <= time; i += tab_step)
{
Tab[0, i / tab_step].Value = x[i];
Tab[1, i / tab_step].Value = y[i];
}
}
}
catch (Exception error)
{
MessageBox.Show($"Ошибка: {error.Message}");
}
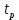 переходного процесса и уменьшению степени затухания.
переходного процесса и уменьшению степени затухания.2.Увеличение коэффициента
 дифференциальной части регулятора приводит к уменьшению времени
дифференциальной части регулятора приводит к уменьшению времени 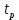 переходного процесса и уменьшению перерегулирования.
переходного процесса и уменьшению перерегулирования.В пропорционально-дифференцируемом алгоритме регулирования (ПД-алгоритм), регулятор работает с опережением, улучшая качество переходного процесса за счет учета тенденции последующего его развития, т. е. увеличивает быстродействие системы и запас устойчивости. Недостатком пропорционально – дифференциального закона регулирования является ограниченная точность.
Список использованных источников
-
Семенов, А. М. Электронное гиперссылочное учебное пособие по дисциплине «Основы теории управления» / А. М.Семенов, И. Б. Крылов. – Оренбург. гос. ун-т, Университетский фонд алгоритмов и программ. – № 521 ; зарегистр. 06.11.09. Мирошник, И. В. Теория автоматического управления. Линейные системы. Учебное пособие для вузов / И.В. Мирошник. – СПб.: Питер, 2005. – 336с. -
Семенов, В. В. Математическая теория управления в примерах и задачах: Учебное пособие для студентов вузов / В. В. Семенов, А. В. Пантелеев, А. С. Бортаковский. – М. : Изд-во МАИ, 1997. – 261 с. -
Семенов, А. М. Исследование типовой САУ. Методические рекомендации по выполнению курсовой работы / А. М. Семенов. – Оренбург: ФВУ, 1999. – 34 c. -
Семенов,А. М. Работоспособность САУ: Учебное пособие / А. М. Семенов, В. В Паничев. – Оренбург : ФВУ, 2002. – 70 с. -
«МВТУ» – программный комплекс для моделирования и исследования систем и объектов. – Режим доступа: сайт http://energy.power.bmstu.ru/mvtu/ -
Дядик, В. Ф. Теория автоматического управления: учебное пособие / В. Ф. Дядик, С. А. Байдали, Н. С. Криницын. − Томск: Изд-во Томского политехнического университета, 2011. – 196 с. -
Пупков, К. А. Методы классической и современной теории автоматического управления : учебник. В 5 т. Т. 1. Математические модели, динамические характеристики и анализ систем автоматического управления / К. А. Пупков, Н. Д. Егупов. – 2-е изд., перераб. и доп. – М. : МГТУ им. Н.Э. Баумана, 2004. – 656 с. -
Цыпкин, Я. З. Основы теории автоматических систем : учеб. пособие для вузов / Я. З. Цыпкин. – М. : Наука, 1977. – 559 с. -
Востриков, А. С. Теория автоматического регулирования : учеб. пособие для вузов / А. С. Востриков, Г. А. Французова. – М. : Высш. шк., 2004. – 365 с. -
Анхимюк, В. Л. Теория автоматического управления: Учеб. пособие для вузов / В. Л. Анхимюк, О. Ф. Опейко, Н. Н. Михеев. – 2-е изд., испр. – Минск: Дизайн ПРО, 2002. – 352 с. -
Юревич, Е. И. Теория автоматического управления / Е. И. Юревич. – СПб. : BHV, 2016. – 560 c. -
Бесекерский, В.А. Теория систем автоматического управления / В. А. Бесекерский, Е. П. Попов. - 4-е изд., перераб. и доп.- CПб.: Профессия, 2004. – 752 с. -
Куропаткин, П. В. Теория автоматического управления: Учеб. пособие для вузов / П. В. Куропаткин ; под ред. Д. В. Васильева. – М. : Высш. школа, 1973. – 528 с. -
Теория автоматического управления : Учеб. пособие для вузов / Под ред. А.С. Щаталова. – М.: Высш. шк., 1977. – 448 с.: ил.
Приложение А
(обязательное)
Код программы
try
{
{
double kp = Convert.ToDouble(KP.Text),
kd = Convert.ToDouble(KD.Text),
k1 = Convert.ToDouble(K1.Text),
k2 = Convert.To Double(K2.Text),
k3 = Convert.ToDouble(K3.Text),
t1 = Convert.ToDouble(T1.Text),
t2 = Convert.ToDouble(T2.Text),
step = Convert.ToDouble(Step.Text),
u = Convert.ToDouble(U.Text),
out_step = 0.01;
int st = 1,
time = Convert.ToInt32(Convert.ToDouble(Time.Text) / Convert.ToDouble(Step.Text));
List
List
double
cd_prev = 0,
cd_next = 0;
List
List
List
List
List
List
int k = 1;
for (int t = 0 + st; t <= time; t += st)
{
x.Add(t * step);
un.Add(u);
err.Add(un[k] - y[k - 1]);
if (k > 1)
cd_next = -(y[k - 1] - y[k - 2]) / step;
else
cd_next = -y[k - 1] / step;
uc.Add(err[k] * kp +
cd_prev * kd
);
uy.Add(uc[k] * k1);
ua1.Add(ua1[k - 1] + step * (k2 / t1 * uy[k] - ua1[k - 1] / t1));
ua2.Add(ua2[k - 1] + step * (k3 / t2 * ua1[k] - ua2[k - 1] / t2));
y.Add(ua2[k]);
k++;
cd_prev = cd_next;
}
chart_graph("Константа", x, un, SeriesChartType.Line);
chart_graph("Переходной график", x, y, SeriesChartType.Line);
chart_graph("Ошибка", x, err, SeriesChartType.Line);
int tab_step = 1;
if (st < out_step)
tab_step = Convert.ToInt32(st / out_step);
Tab.RowCount = time / tab_step + 1;
for (int i = 0; i <= time; i += tab_step)
{
Tab[0, i / tab_step].Value = x[i];
Tab[1, i / tab_step].Value = y[i];
}
}
}
catch (Exception error)
{
MessageBox.Show($"Ошибка: {error.Message}");
}