Файл: Литература по теме развитие математических умений, раскрываются условия развития математических умений младших школьников посредством игровой деятельности.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 62
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2.
Таким образом, анализ происходит от практического к чувственному, только потом к умственному. Частичный анализ постепенно становится комплексным и системным. Операции же синтеза происходят от простого суммирующего к более сложному. Таким образом действиями анализа младшие школьники овладевают быстрее, чем синтеза. Стоит так же отметить, что действия анализа и синтеза являются взаимосвязанными.
Такой важный мыслительный процесс как сравнение у младших школьников так же развивается от простого, основанного на внешних проявлениях понятий к более системному и планомерному. Стоит отметить, что для детей младшего школьного возраста характерно при сравнении знакомых предметов замечать сходства, а при рассмотрении новых - различи.
До семилетнего возраста, согласно исследованиям психологов занимающихся проблемами возрастной психологии (А.Г. Асмолова, Ж. Пиаже, Д.Б. Эльконина и др.) для детей свойственно репродуктивное мышление, а образы зачастую статичные. Так, например, детям сложно представить положение палочки в полёте. В процессе обучения дети знакомятся с образованием понятий, что в последствии позволяет им строить рассуждения и умозаключения.
В работе Л.С. Выготского «Мышление и речь» описываются трудности овладения детьми общими понятиями. В частности автором отмечено, что на определенной стадии развития подобные отношения общности между понятиями вообще недоступны для ребенка. «Появления первого высшего понятия, стоящего над рядом прежде образованных понятий, появление первого слова типа «мебель» или «одежда», не менее важный симптом прогресса в развитии смысловой стороны детской речи, чем появление первого осмысленного слова» 3.
Психологи так же отмечают, что ребёнку сложно проводить рассуждения от следствия к причине, потому что при умозаключениях от причин к следствию устанавливается прямая связь, а при умозаключениях от фактов к причине – косвенная. Так например, причина может быть следствием нескольких взаимосвязанных фактов, которые должны подвергаться анализу, а это сложно для младшего школьника. Ему проще сказать, что будет если, чем почему это произошло.
Исследования В.В. Давыдова между тем показывают, что у младших школьников могут быть сформированы основы теоретического мышления. Теоретическое мышление, как подчёркивает автор формируется на основе эмпирического. У детей методом проб и ошибок формируется рефлексия и со временем умение выстраивать внутренний план действий.
Итак, сформированные в процессе обучения общие понятия в конечном итоге приводят детей к тому, что они рассматривают явления ни только по внешним признакам, а рассматривают внутренний, понятийный. Таким образом происходит переход от наглядно-образного к теоретическому мышлению.
Развитие восприятия и произвольности, характерные для данного возрастного периода способствуют тому, что дети овладевают абстрактным, теоретическим мышлением, способны к рефлексии своих действий.
О развитии критического мышления у младших школьников свидетельствуют развитые умения находить у себя ошибки и ложные факты отличать от истинных.
Таким образом, анализ психолого-педагогических исследований проблем детского мышления, психологии возрастного развития в трудах В.В. Давыдова, Л.С. Выготского, Р. С. Немова, и других, позволяет называть младший школьный возраст сенситивным для развития навыков устного счёта.
О.А. Ивашова, М.А. Бантова, Н.Б. Истомина, А.А. Столяр, Я.Ф. Чекмарёва, О.П. Зайцева, А.Я. Бурлыга, К.А. Зимовец и другие исследователи считают, что математические умения в свою очередь влияют на умственное развитие личности в целом. Наиболее сенситивным для формирования математических умений считается младший школьный возраст.
Этапы формирования умения математического счета выделены И.А. Гришановой4. Первый этап– это достаточно хорошая и уверенная степень овладения каким-либо умением. При овладении умением в вычислениях или тождественных преобразованиях первые упражнения на применение нового приема, метода, определения должны выполняться с подробными объяснениями и приведением конкретных поясняющих примеров. Второй этап – этап автоматизации умения. Автоматизация умения происходит путем исключения некоторых промежуточных операций. Поэтому следует помочь учащимся перейти от сложной схемы действий к более простой.
Умения применения устного счёта у обучающихся на всех этапах изучения курса математики в начальной школе является основой формирования вычислительной культуры. Качество вычислительных умений определяется знанием алгоритмов вычислений. Поэтому степень овладения вычислительными умениями зависит от четкости сформулированного алгоритма и от понимания принципа его использования. Умение формируется в процессе выполнения целенаправленной системы упражнений. Очень важно владение некоторыми вычислительными умениями доводить до навыков.
По мнению Э.В. Маклаевой, Е.К. Дмитриевой: «Формирование любого вычислительного действия является стабильным и эффективным только в том случае, если школьник сам прилагает ряд усилий и проявляет интерес к получаемому результату»
5. При этом им может быть использован алгоритм действия, выполнение всех операций расчетного характера. Формирование вычислительных умений и навыков, как одного из видов деятельности у младших школьников тесным образом связано с формированием компетенций. В отличие от них компетенция – это более осознанная форма деятельности, которая в своей структуре опирается на некий комплекс развитых у обучающихся качеств личности. Формирование вычислительных умений и навыков у школьников остается одной из основных задач математического обучения, так как вычислительные умения и навыки необходимы для выполнения преобразований в любой части математики. Учащиеся, успешно овладевшие вычислительными навыками, смогут успешно изучить все предметы в школьной программе, не прилагая огромного усилия.
Формирование вычислительных умений и навыков является одной из основных задач, которые должны быть решены в процессе обучения детей в начальной школе. Эти умения и навыки должны быть сформированы сознательно и твердо, так как они основаны на математике в течение всего начального процесса, который включает в себя формирование вычислительных умений и навыков, основанных на сознательном использовании вычислительных технологий. Последнее стало возможным благодаря тому, что программа включает в себя ознакомление с некоторыми наиболее важными свойствами арифметических операций и их следствиями. Вычислительные умения и навыки определяются как высокая степень мастерства в вычислительной технике.
А.В. Белошистая утверждает: «Для получения вычислительных умений и навыков в каждом случае важно знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметической операции и выполнить эти операции достаточно быстро»6.
Вычислительные умения и навыки считаются одним из видов умений и навыков обучения, которые играют определенную роль и постоянно развиваются в процессе обучения. Они являются частью структуры учебно-познавательной деятельности, которая существует в образовательной деятельности, осуществляемой с помощью системы операций. Вычислительные умения и навыки, которыми должен обладать младший школьник имеют следующие характеристики: правильность, осознанность, рациональность, обобщенность, автоматизм и прочность. При этом устные вычисления, как правило, являются ключевыми и первостепенными в данном процессе. Устные упражнения могут варьироваться по форме, содержанию и сложности и могут быть тренировочными, контролирующими или обобщающими. Устные упражнения играют важную роль в повышении вычислительных умений и навыков школьников и эффективности урока.
М.А. Бантова считает: «Важно, какие упражнения были выбраны для каждой темы, в какое время»7Прививая любовь к устным расчетам, учитель помогает ученикам активно действовать в учебном материале, пробуждая их желание совершенствовать методы расчета и решения проблем, заменяя менее рациональные и более современные, что является важным условием для осознания того, что учащиеся нуждаются в обучении. Устные упражнения очень важны, потому что: - Они активируют психическую активность школьников; - В проявлениях детей развивается память, речь, внимание, способность воспринимать высказывания на слух, быстрая реакция. - Опыт показывает, что при умелом применении устных упражнений они могут играть важную роль в повышении эффективности уроков. Основным условием является рассмотрение устного счета не как дополнительного материала, а как органично необходимой части уроков, без усвоения этих знаний и умений и навыков будет очень сложно, а потери времени еще больше. Устная работа на уроках математики очень важна – это разговор учителя с классом или с отдельными учениками, и рассуждения ученика при выполнении определенных задач, и так далее. Тот момент, когда ученик проговаривает или по-другому сказать комментирует свою деятельность, очень положительно влияет на память. В этих видах устной работы есть так называемые устные упражнения. Ранее они в основном сводились к расчетам, поэтому им присваивалось название «устный счет».
Э.В. Маклаева, С.А. Чернышова считают: «Несмотря на то, что в современных программах содержание устных упражнений достаточно разнообразно и велико благодаря введению алгебраических и геометрических материалов, а также из-за большого внимания к оперативным свойствам чисел и таким вопросам, как значение, так называемый «устный счет» по отношению к устным формам упражнений сохранились до наших дней»8.
Изучая психолого-педагогические условия формирования вычислительных навыков у младших школьников, можно сделать выводы о том, что одним из эффективных средств решения данной проблемы является использование игровых технологий.
Понятие игровой деятельности в педагогике не ново. Изучением данной проблемы занимались такие ученые как Немов, Рубинштейн, Карл Юнг, Зигмунд Фрейд и так далее. В общепринятом смысле игровая деятельность представляет собой ведущий вид деятельности детей. Различают несколько типов игровой деятельности: сюжетно-ролевая игра, дидактическая игра, игры с предметами.
В качестве характеристик игры выступает её двуплановость, которая присуща также драматическому искусству. Двуплановость проявляется в том, что играющий выполняет определённые действия, тратит энергию на решение конкретных, чаще всего нестандартных задач. В то же время момент этой деятельности носит условный характер, что позволяет игроку отвлечься от реальных ситуаций.
Игровые приёмы в педагогике являются методами активного обучения и представляют собой отдельные игровые действия, непродолжительные по времени с чёткими правилами и контролем, нацеленные на освоение и отработку вычислительных навыков9. Среди традиционных игровых приёмов формирования математических умений можно выделить:
Рассмотрим каждый игровой прём подробнее. Приём «Продолжи ряд» представлен в большинстве УМК по математике в начальной школе (Рисунок 1). Детям предлагается последовательность чисел, в которой каждое число закономерно связано с предыдущим. Задача обучающихся состоит в поиске закономерности и нахождении нескольких последующих чисел. Как правило числа увеличиваются либо уменьшаются на несколько единиц, либо сотен, тысяч (в зависимости от тех образовательных задач, которые стоят на каждом конкретном уроке), а также в несколько раз. Данный приём требует от обучающихся выполнения устных вычислений, хотя конкретно такая задача не ставится, таким образом, достигается необходимый уровень отвлечённости и в тоже время осознанности для формирования навыка устного счёта. Существует так же и вариации данного приёма, когда требуется добавить пропущенные числа, либо найти лишнее в ряду число.
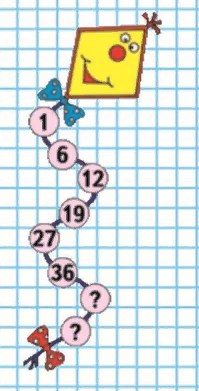

Рисунок 1 – Игровой приём «Продолжи ряд» на страницах учебника М.И. Моро «Математика. 3 класс» (слева) и Г.В. Дорофеевой «Математика. 3 класс» (справа).
Приём числовые домики так же имеет несколько вариаций. Предлагается схематическое изображение в виде домика. В крыше располагается число, на «этажах» два окошка, одно из которых пустое, а второе заполнено числом. Дети должны заполнить пустые «окошки» числами в соответствии с учебной задачей: повторяется состав числа, либо отрабатываются вычислительные навыки. Домик может быть пустым, а учащиеся должны его самостоятельно заполнить, либо заполненным, и детям необходимо «набрать» называя или выделяя нужные окошки заданное число (Рисунок 2).
Таким образом, анализ происходит от практического к чувственному, только потом к умственному. Частичный анализ постепенно становится комплексным и системным. Операции же синтеза происходят от простого суммирующего к более сложному. Таким образом действиями анализа младшие школьники овладевают быстрее, чем синтеза. Стоит так же отметить, что действия анализа и синтеза являются взаимосвязанными.
Такой важный мыслительный процесс как сравнение у младших школьников так же развивается от простого, основанного на внешних проявлениях понятий к более системному и планомерному. Стоит отметить, что для детей младшего школьного возраста характерно при сравнении знакомых предметов замечать сходства, а при рассмотрении новых - различи.
До семилетнего возраста, согласно исследованиям психологов занимающихся проблемами возрастной психологии (А.Г. Асмолова, Ж. Пиаже, Д.Б. Эльконина и др.) для детей свойственно репродуктивное мышление, а образы зачастую статичные. Так, например, детям сложно представить положение палочки в полёте. В процессе обучения дети знакомятся с образованием понятий, что в последствии позволяет им строить рассуждения и умозаключения.
В работе Л.С. Выготского «Мышление и речь» описываются трудности овладения детьми общими понятиями. В частности автором отмечено, что на определенной стадии развития подобные отношения общности между понятиями вообще недоступны для ребенка. «Появления первого высшего понятия, стоящего над рядом прежде образованных понятий, появление первого слова типа «мебель» или «одежда», не менее важный симптом прогресса в развитии смысловой стороны детской речи, чем появление первого осмысленного слова» 3.
Психологи так же отмечают, что ребёнку сложно проводить рассуждения от следствия к причине, потому что при умозаключениях от причин к следствию устанавливается прямая связь, а при умозаключениях от фактов к причине – косвенная. Так например, причина может быть следствием нескольких взаимосвязанных фактов, которые должны подвергаться анализу, а это сложно для младшего школьника. Ему проще сказать, что будет если, чем почему это произошло.
Исследования В.В. Давыдова между тем показывают, что у младших школьников могут быть сформированы основы теоретического мышления. Теоретическое мышление, как подчёркивает автор формируется на основе эмпирического. У детей методом проб и ошибок формируется рефлексия и со временем умение выстраивать внутренний план действий.
Итак, сформированные в процессе обучения общие понятия в конечном итоге приводят детей к тому, что они рассматривают явления ни только по внешним признакам, а рассматривают внутренний, понятийный. Таким образом происходит переход от наглядно-образного к теоретическому мышлению.
Развитие восприятия и произвольности, характерные для данного возрастного периода способствуют тому, что дети овладевают абстрактным, теоретическим мышлением, способны к рефлексии своих действий.
О развитии критического мышления у младших школьников свидетельствуют развитые умения находить у себя ошибки и ложные факты отличать от истинных.
Таким образом, анализ психолого-педагогических исследований проблем детского мышления, психологии возрастного развития в трудах В.В. Давыдова, Л.С. Выготского, Р. С. Немова, и других, позволяет называть младший школьный возраст сенситивным для развития навыков устного счёта.
О.А. Ивашова, М.А. Бантова, Н.Б. Истомина, А.А. Столяр, Я.Ф. Чекмарёва, О.П. Зайцева, А.Я. Бурлыга, К.А. Зимовец и другие исследователи считают, что математические умения в свою очередь влияют на умственное развитие личности в целом. Наиболее сенситивным для формирования математических умений считается младший школьный возраст.
Этапы формирования умения математического счета выделены И.А. Гришановой4. Первый этап– это достаточно хорошая и уверенная степень овладения каким-либо умением. При овладении умением в вычислениях или тождественных преобразованиях первые упражнения на применение нового приема, метода, определения должны выполняться с подробными объяснениями и приведением конкретных поясняющих примеров. Второй этап – этап автоматизации умения. Автоматизация умения происходит путем исключения некоторых промежуточных операций. Поэтому следует помочь учащимся перейти от сложной схемы действий к более простой.
Умения применения устного счёта у обучающихся на всех этапах изучения курса математики в начальной школе является основой формирования вычислительной культуры. Качество вычислительных умений определяется знанием алгоритмов вычислений. Поэтому степень овладения вычислительными умениями зависит от четкости сформулированного алгоритма и от понимания принципа его использования. Умение формируется в процессе выполнения целенаправленной системы упражнений. Очень важно владение некоторыми вычислительными умениями доводить до навыков.
По мнению Э.В. Маклаевой, Е.К. Дмитриевой: «Формирование любого вычислительного действия является стабильным и эффективным только в том случае, если школьник сам прилагает ряд усилий и проявляет интерес к получаемому результату»
5. При этом им может быть использован алгоритм действия, выполнение всех операций расчетного характера. Формирование вычислительных умений и навыков, как одного из видов деятельности у младших школьников тесным образом связано с формированием компетенций. В отличие от них компетенция – это более осознанная форма деятельности, которая в своей структуре опирается на некий комплекс развитых у обучающихся качеств личности. Формирование вычислительных умений и навыков у школьников остается одной из основных задач математического обучения, так как вычислительные умения и навыки необходимы для выполнения преобразований в любой части математики. Учащиеся, успешно овладевшие вычислительными навыками, смогут успешно изучить все предметы в школьной программе, не прилагая огромного усилия.
Формирование вычислительных умений и навыков является одной из основных задач, которые должны быть решены в процессе обучения детей в начальной школе. Эти умения и навыки должны быть сформированы сознательно и твердо, так как они основаны на математике в течение всего начального процесса, который включает в себя формирование вычислительных умений и навыков, основанных на сознательном использовании вычислительных технологий. Последнее стало возможным благодаря тому, что программа включает в себя ознакомление с некоторыми наиболее важными свойствами арифметических операций и их следствиями. Вычислительные умения и навыки определяются как высокая степень мастерства в вычислительной технике.
А.В. Белошистая утверждает: «Для получения вычислительных умений и навыков в каждом случае важно знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметической операции и выполнить эти операции достаточно быстро»6.
Вычислительные умения и навыки считаются одним из видов умений и навыков обучения, которые играют определенную роль и постоянно развиваются в процессе обучения. Они являются частью структуры учебно-познавательной деятельности, которая существует в образовательной деятельности, осуществляемой с помощью системы операций. Вычислительные умения и навыки, которыми должен обладать младший школьник имеют следующие характеристики: правильность, осознанность, рациональность, обобщенность, автоматизм и прочность. При этом устные вычисления, как правило, являются ключевыми и первостепенными в данном процессе. Устные упражнения могут варьироваться по форме, содержанию и сложности и могут быть тренировочными, контролирующими или обобщающими. Устные упражнения играют важную роль в повышении вычислительных умений и навыков школьников и эффективности урока.
М.А. Бантова считает: «Важно, какие упражнения были выбраны для каждой темы, в какое время»7Прививая любовь к устным расчетам, учитель помогает ученикам активно действовать в учебном материале, пробуждая их желание совершенствовать методы расчета и решения проблем, заменяя менее рациональные и более современные, что является важным условием для осознания того, что учащиеся нуждаются в обучении. Устные упражнения очень важны, потому что: - Они активируют психическую активность школьников; - В проявлениях детей развивается память, речь, внимание, способность воспринимать высказывания на слух, быстрая реакция. - Опыт показывает, что при умелом применении устных упражнений они могут играть важную роль в повышении эффективности уроков. Основным условием является рассмотрение устного счета не как дополнительного материала, а как органично необходимой части уроков, без усвоения этих знаний и умений и навыков будет очень сложно, а потери времени еще больше. Устная работа на уроках математики очень важна – это разговор учителя с классом или с отдельными учениками, и рассуждения ученика при выполнении определенных задач, и так далее. Тот момент, когда ученик проговаривает или по-другому сказать комментирует свою деятельность, очень положительно влияет на память. В этих видах устной работы есть так называемые устные упражнения. Ранее они в основном сводились к расчетам, поэтому им присваивалось название «устный счет».
Э.В. Маклаева, С.А. Чернышова считают: «Несмотря на то, что в современных программах содержание устных упражнений достаточно разнообразно и велико благодаря введению алгебраических и геометрических материалов, а также из-за большого внимания к оперативным свойствам чисел и таким вопросам, как значение, так называемый «устный счет» по отношению к устным формам упражнений сохранились до наших дней»8.
Изучая психолого-педагогические условия формирования вычислительных навыков у младших школьников, можно сделать выводы о том, что одним из эффективных средств решения данной проблемы является использование игровых технологий.
-
Игровая деятельность как средство развития математических умений у младших школьников
Понятие игровой деятельности в педагогике не ново. Изучением данной проблемы занимались такие ученые как Немов, Рубинштейн, Карл Юнг, Зигмунд Фрейд и так далее. В общепринятом смысле игровая деятельность представляет собой ведущий вид деятельности детей. Различают несколько типов игровой деятельности: сюжетно-ролевая игра, дидактическая игра, игры с предметами.
В качестве характеристик игры выступает её двуплановость, которая присуща также драматическому искусству. Двуплановость проявляется в том, что играющий выполняет определённые действия, тратит энергию на решение конкретных, чаще всего нестандартных задач. В то же время момент этой деятельности носит условный характер, что позволяет игроку отвлечься от реальных ситуаций.
Игровые приёмы в педагогике являются методами активного обучения и представляют собой отдельные игровые действия, непродолжительные по времени с чёткими правилами и контролем, нацеленные на освоение и отработку вычислительных навыков9. Среди традиционных игровых приёмов формирования математических умений можно выделить:
-
«Продолжи ряд»; -
«Числовые домики»; -
«Магический квадрат»; -
«Числовая цепочка»; -
«Составь поезд»; -
«Арифметические ребусы»; -
И другие.
Рассмотрим каждый игровой прём подробнее. Приём «Продолжи ряд» представлен в большинстве УМК по математике в начальной школе (Рисунок 1). Детям предлагается последовательность чисел, в которой каждое число закономерно связано с предыдущим. Задача обучающихся состоит в поиске закономерности и нахождении нескольких последующих чисел. Как правило числа увеличиваются либо уменьшаются на несколько единиц, либо сотен, тысяч (в зависимости от тех образовательных задач, которые стоят на каждом конкретном уроке), а также в несколько раз. Данный приём требует от обучающихся выполнения устных вычислений, хотя конкретно такая задача не ставится, таким образом, достигается необходимый уровень отвлечённости и в тоже время осознанности для формирования навыка устного счёта. Существует так же и вариации данного приёма, когда требуется добавить пропущенные числа, либо найти лишнее в ряду число.


Рисунок 1 – Игровой приём «Продолжи ряд» на страницах учебника М.И. Моро «Математика. 3 класс» (слева) и Г.В. Дорофеевой «Математика. 3 класс» (справа).
Приём числовые домики так же имеет несколько вариаций. Предлагается схематическое изображение в виде домика. В крыше располагается число, на «этажах» два окошка, одно из которых пустое, а второе заполнено числом. Дети должны заполнить пустые «окошки» числами в соответствии с учебной задачей: повторяется состав числа, либо отрабатываются вычислительные навыки. Домик может быть пустым, а учащиеся должны его самостоятельно заполнить, либо заполненным, и детям необходимо «набрать» называя или выделяя нужные окошки заданное число (Рисунок 2).