ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 33
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
 ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики
(наименование института полностью)
Кафедра /департамент /центр1промышленная электроника
(наименование кафедры/департамента/центра полностью)
13.03.02.
(код и наименование направления подготовки, специальности)
Электроэнергетика электротехника. Электроснабжение
(направленность (профиль) / специализация)
Практическое задание № 1
по учебному курсу «Высшая математика 2
»
(наименование учебного курса)
| Студент | Исаев Данил Сергеевич | |
| | (И.О. Фамилия) | |
| Группа | ЭЭТбп-1901б | |
| | | |
| Преподаватель |
| |
| | (И.О. Фамилия) | |
Контрольная 1 Вариант 3
Найти производные y´=
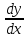 заданных функций
заданных функцийЗадача 1
Дана функция Y=
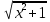 - ln
- ln 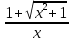
Пошаговое решение
Разность формула
(u−v)′=u′−v′
(
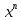
)′=n⋅
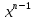
(
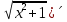 =
=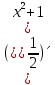 =
=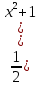 =
=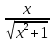
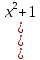
Формула ( ln u)´=
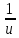 U´
U´(ln
 )´=
)´= 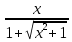 (
( )´
)´ Найдем
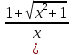 )´ по формуле (
)´ по формуле ( 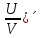 =
= 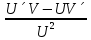
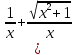 )´= (
)´= ( 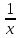 )´+(
)´+( 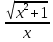 )´ =
)´ =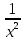 +
+ 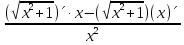 =
=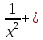
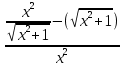 =
= 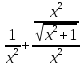 -
- 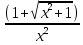
=
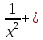
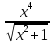 -
- 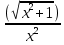 ⇒
⇒ (ln
 )´=
)´= 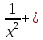
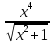 -
- 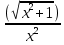
(
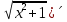 =
=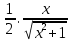 ·2x=
·2x=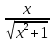
Ответ y´=
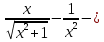
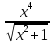
+
 или
или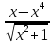 -
-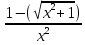
Задача 2
Вычислить производную:
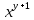 =
= 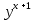
Решение:
Переносим
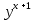 в левую часть уравнения:
в левую часть уравнения: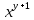 =
= 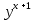
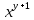 -
- 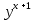 =0
=0 Производная разности равна разности производных:
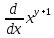 -
-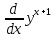
Вычислим производную:
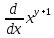
Используем правило дифференцирования сложной функции
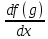 =
= 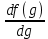 ∙
∙ 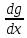
Где d(
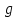 )=
)=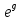
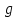 =(y+1)∙
=(y+1)∙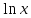
Подставляем
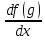 =
= 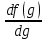 ∙
∙ 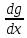
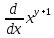 =
= 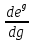 ∙
∙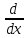 (y+1)
(y+1)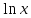 , но
, но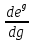 =
=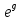
=
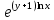 =
=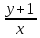 =
= 
Получим
 ·
· ((y+1)∙
((y+1)∙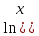
Используем формулу для вычисления производной произведения:
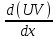 =
=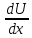 V +
V +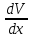 U , где U=y+1 V=
U , где U=y+1 V=
 (
(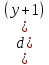 ∙
∙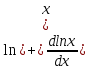
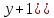 =
= (
(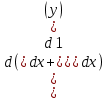 ∙∙
∙∙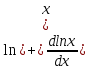
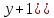 =
=Производная суммы равна сумме производных:
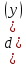 =y′
=y′ 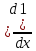 =0
=0 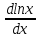 =
=
=
 (
(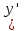 ∙
∙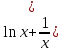
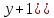 =
= (
(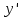 ∙
∙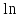 x +
x +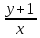 )
) Вычислим производную:

Используем правило дифференцирования сложной функции

=
 ∙
∙ 
Где d(
 )=
)=
 =(x+1)∙
=(x+1)∙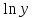
Подставляем
 =
=  ∙
∙ 
 =
=  ∙
∙ (x+1)
(x+1)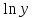 , но
, но =
= =
=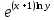 =
=
Получим
 ·
· ((x+1)∙
((x+1)∙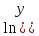
Используем формулу для вычисления производной произведения:
 =
= V +
V + U , где U=x+1 V=
U , где U=x+1 V=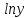
 ·
·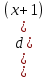 ∙
∙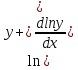
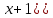 =
= ·(
·(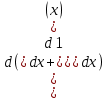 ∙
∙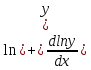
 =
=Производная суммы равна сумме производных: