ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 34
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=1  =0
=0 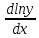 =0
=0
= ·
· Получили следующее уравнение:
Получили следующее уравнение:
 (
( ∙
∙ x +
x + )-
)-  ·
· y = 0
y = 0
Выражаем из этого уравнения y´
 (
( ∙
∙ x +
x +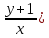 =
=  +
+ y
y
 ·
·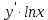 +
+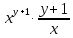 =
= +
+ y
y
 ·
·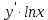 =
= +
+ y-
y-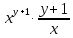
 =
=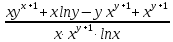
Задача 3
Дана функция Y=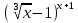
Вычисляем производную:
Ln y =(x+1) Ln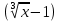 ⇒
⇒
(Ln y)´ =((x+1) Ln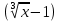 )´
)´
Используя свойства логарифма, осуществляем преобразования:
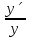
=(x+1)´ Ln +(x+1)( Ln
+(x+1)( Ln )´
)´
Используем правило дифференцирования сложной функции:
( Ln )´=
)´=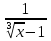 ·
· ´
´
Производная разности равна разности производных:
(U+V-W)´=U´+V´-W´
 ´=
´=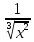 ·
·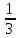 – 0
– 0
Подставляем
( Ln )´=
)´=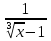 ·
·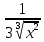 =
=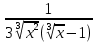
 =(x+1)´ Ln
=(x+1)´ Ln +(x+1)( Ln
+(x+1)( Ln )´ = Ln
)´ = Ln +(x+1)
+(x+1)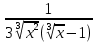
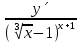 = Ln
= Ln +(x+1) )
+(x+1) )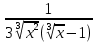
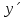 =
= (Ln
(Ln +(x+1) )
+(x+1) )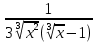
2
Используя правила Лопиталя вычислить представленные пределы
Задание 1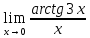
При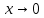
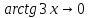
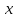
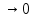
У нас есть неопределённость типа 0/0
т.к. для числителя предел
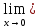
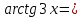 0
0
для знаменателя предел
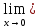 (x)=0
(x)=0
Возьмем производные от числителя и знаменателя

(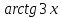 )′=
)′= 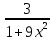
x′=1
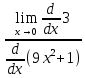 =
= 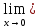 (3)=3 ⇒
(3)=3 ⇒
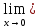 (3)= 3
(3)= 3
Задание №2
Используя правила Лопиталя вычислить представленные пределы
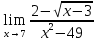
У нас есть неопределённость типа 0/0
т.к. для числителя предел
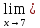 (
(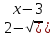 =(
=(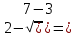 0
0
для знаменателя предел
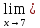 (
(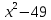 )=0
)=0
Возьмем производные от числителя и знаменателя
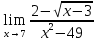
(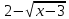 ))′= -
))′= -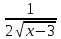
(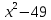 )′=2x
)′=2x
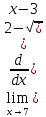 =-
=- 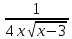 =
=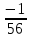
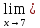 =
= 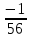
Задание №3
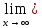 (
(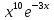 )
)
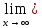 (
(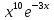 )=
)= 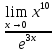
При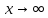
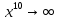
При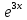
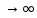
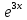
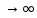 ⇒
⇒
 (
( ) =0
) =0
1 Оставить нужное
 =0
=0 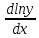 =0
=0=
 ·
· Получили следующее уравнение:
Получили следующее уравнение: (
( ∙
∙ x +
x + )-
)-  ·
· y = 0
y = 0Выражаем из этого уравнения y´
 (
( ∙
∙ x +
x +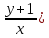 =
=  +
+ y
y  ·
·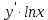 +
+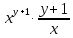 =
= +
+ y
y  ·
·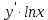 =
= +
+ y-
y-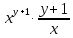
 =
=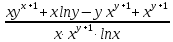
Задача 3
Дана функция Y=
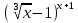
Вычисляем производную:
Ln y =(x+1) Ln
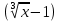 ⇒
⇒ (Ln y)´ =((x+1) Ln
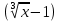 )´
)´Используя свойства логарифма, осуществляем преобразования:
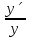
=(x+1)´ Ln
 +(x+1)( Ln
+(x+1)( Ln )´
)´Используем правило дифференцирования сложной функции:
( Ln
 )´=
)´=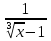 ·
· ´
´ Производная разности равна разности производных:
(U+V-W)´=U´+V´-W´
 ´=
´=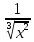 ·
·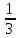 – 0
– 0 Подставляем
( Ln
 )´=
)´=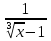 ·
·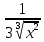 =
=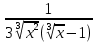
 =(x+1)´ Ln
=(x+1)´ Ln +(x+1)( Ln
+(x+1)( Ln )´ = Ln
)´ = Ln +(x+1)
+(x+1)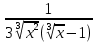
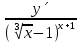 = Ln
= Ln +(x+1) )
+(x+1) )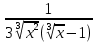
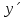 =
= (Ln
(Ln +(x+1) )
+(x+1) )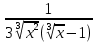
2
Используя правила Лопиталя вычислить представленные пределы
Задание 1
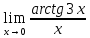
При
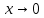
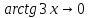
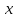
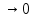
У нас есть неопределённость типа 0/0
т.к. для числителя предел
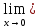
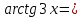 0
0для знаменателя предел
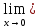 (x)=0
(x)=0Возьмем производные от числителя и знаменателя

(
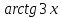 )′=
)′= 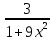
x′=1
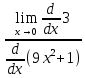 =
= 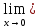 (3)=3 ⇒
(3)=3 ⇒ 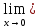 (3)= 3
(3)= 3Задание №2
Используя правила Лопиталя вычислить представленные пределы
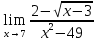
У нас есть неопределённость типа 0/0
т.к. для числителя предел
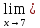 (
(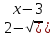 =(
=(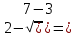 0
0для знаменателя предел
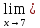 (
(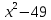 )=0
)=0Возьмем производные от числителя и знаменателя
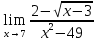
(
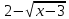 ))′= -
))′= -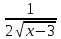
(
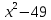 )′=2x
)′=2x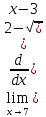 =-
=- 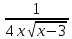 =
=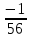
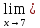 =
= 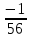
Задание №3
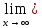 (
(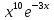 )
)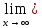 (
(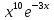 )=
)= 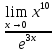
При
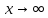
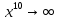
При
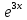
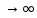
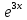
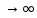 ⇒
⇒ (
( ) =0
) =01 Оставить нужное