Файл: Лабораторная работа проверка закона Ома для цепей переменного тока.doc

Лабораторная работа

проверка закона Ома для цепей переменного тока

Цель работы: Экспериментальное определение индуктивности, ёмкости и проверка закона Ома для цепей переменного тока.

Оборудование: катушка индуктивности и два конденсатора, реостат, источник постоянного и переменного напряжения, мультиметры в качестве вольтметра и амперметра, соединительные проводники.

КРАТКАЯ ТЕОРИЯ.

Если к концам проводника с активным сопротивлением приложена переменная электродвижущая сила, величина которой в каждый момент времени определяется уравнением

U = U_mcost, (1)

где U_m - амплитуда, а  - круговая частота, то в нем возникает переменный электрический ток, сила которого в тот же момент времени определяется по закону Ома:

. (2)

Если же, помимо сопротивления R, в цепи имеется индуктивность, характеризуемая коэффициентом самоиндукции L, то под действием той же электродвижущей силы возникает ток силой

. (3)

где - сдвиг фаз между током и напряжением, определяемый из формулы

. (4)

Из сопоставления уравнений (1) и (3) следует, что в этом случае ток отстает по фазе от напряжения.

Величина носит название полного сопротивления (импеданс), так как она играет в формуле (4) ту же роль, что и обычное активное сопротивление R в формуле закона Ома. Величина же L называется индуктивным сопротивлением.

Если вместо индуктивности в цепь переменного тока включена ёмкость С, то сила тока выражается формулой

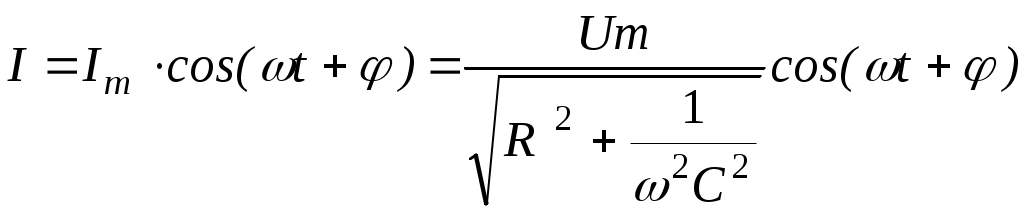, (5)

а

. (6)

В этом случае сила тока опережает по фазе напряжение. Полное сопротивление цепи Z₂ теперь запишется как , причем величина 1/(С) называется

---

ёмкостным сопротивлением.

Наконец, в случае, когда в цепь включены последовательно все три величины - R, L и С, сила тока в цепи может быть записана выражением

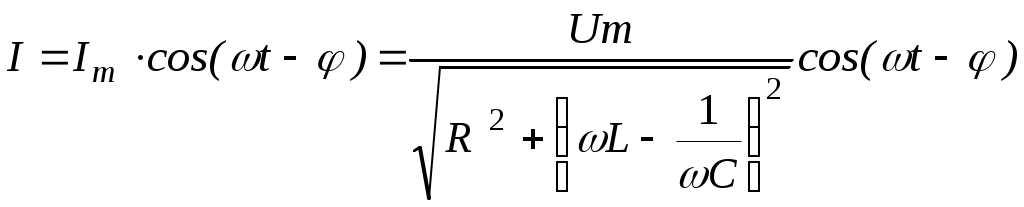. (7а)

(7б)

При этом полное сопротивление равно .

Выражение (7) носит название формулы закона Ома для переменного тока.

В формулы (2), (3), (5) и (7) входят I_m и U_m – максимальные (амплитудные) значения токов и напряжений. Так как измеряемые приборами эффективные значения этих величин, I_эфф и U_эфф, связаны с максимальными посредством формул:

и ,

то, подставляя отсюда I_m и U_m в вышеуказанные формулы, получим:

, (8)

(9)

(10)

(11)

Во всех этих формулах под R следует подразумевать сумму всех активных сопротивлений цепи (в том числе и катушки индуктивности), на концах которой измеряется электродвижущая сила. Если разность потенциалов измеряется непосредственно на зажимах катушки, то R есть активное сопротивление одной лишь катушки.

ПРАКТИЧЕСКАЯ ЧАСТЬ

Упражнение 1. Измерение коэффициента самоиндукции.

Из формулы (9) следует, что

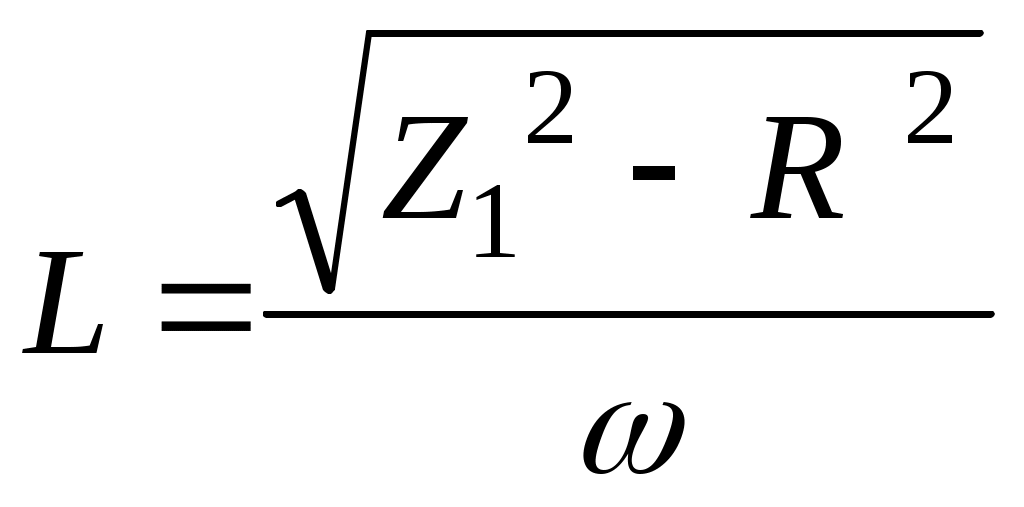, (12)

где активное сопротивление:

R = U_пост/I_пост , (13)

а полное сопротивление:

Z₁ = U_эфф/I_эфф .(14)




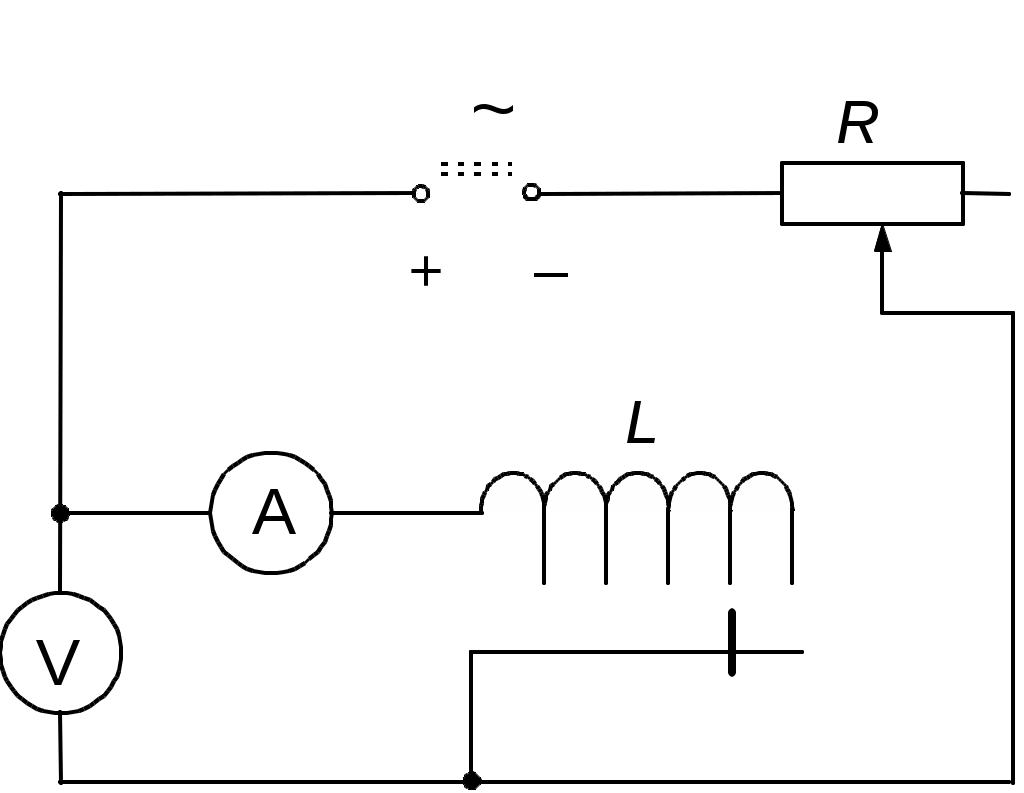
Рис.1.
Определив величины Z₁, R, , найдем, очевидно, и L. Для этого катушка с неизвестным коэффициентом самоиндукции L и активным сопротивлением

---

R, реостат r и амперметр А соединяются последовательно (рис.1) и подключаются к средним клеммам перекидного ключа К, к крайним клеммам которого подведены с разных сторон постоянный и переменный токи.

Для определения  необходимо знать период переменного тока. Если этот ток берут от городской сети, то для большинства городов России Т = 1/50 с и, следовательно,

.

Порядок выполнения.

1. Для измерения активного сопротивления катушки устанавливают ползунок реостата на максимум сопротивления и, присоединив вольтметр, замыкают ключ К на постоянный ток. Медленно передвигая ползунок реостата, устанавливают его в такое положение, чтобы стрелка амперметра дала достаточное для отсчета отклонение.

Измерив затем по приборам силу тока I_пост и напряжение U_пост, изменяют переключением контактов число работающих витков катушки и производят дальнейшие измерения.

Проделав эти измерения для каждого контакта не менее трех раз, подставляют средние результаты измерения в формулу (13) и вычисляют значения активных сопротивлений для каждого из контактов катушки.

При измерениях необходимо иметь в виду следующее:

а) ключ не следует держать включенным дольше, чем это необходимо для производства отсчётов, так как в противном случае катушка нагревается и сопротивление ее значительно изменится;

б) переключение витков катушки L следует производить при полностью введенном в цепь сопротивлении реостата.

2. Для определения полного сопротивления катушки L замыкают ключ К на переменный ток.

Изменяя положение движка реостата, устанавливают, как и прежде, достаточное отклонение стрелки амперметра. Произведя соответствующие отсчёты, изменяют число работающих витков катушки и, действуя далее совершенно аналогично предыдущему, получают для каждого контакта необходимые значения I_эфф и U_эфф, подставляя которые в формулу (14), вычисляют соответствующие значения сопротивления Z₁.

Определяя таким образом значения R и Z₁, находят при помощи формулы (12) значения L

---

, а затем при помощи формулы (4) - значения угла фазового сдвига  для каждого из контактов катушки.

Упражнение 2. Измерение емкости конденсаторов.

Из формулы (11) следует, что

,

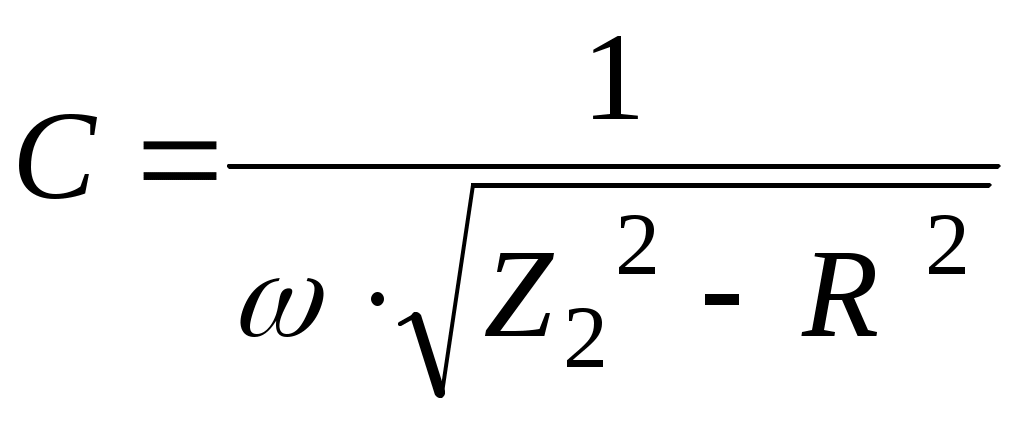где Z₂ и R – соответственно полное и активное сопротивление цепи.

В случае, когда напряжение U_эфф измеряется непосредственно на обкладках конденсатора, можно считать, что активное сопротивление в цепи отсутствует (R = 0), поэтому:

. (15)




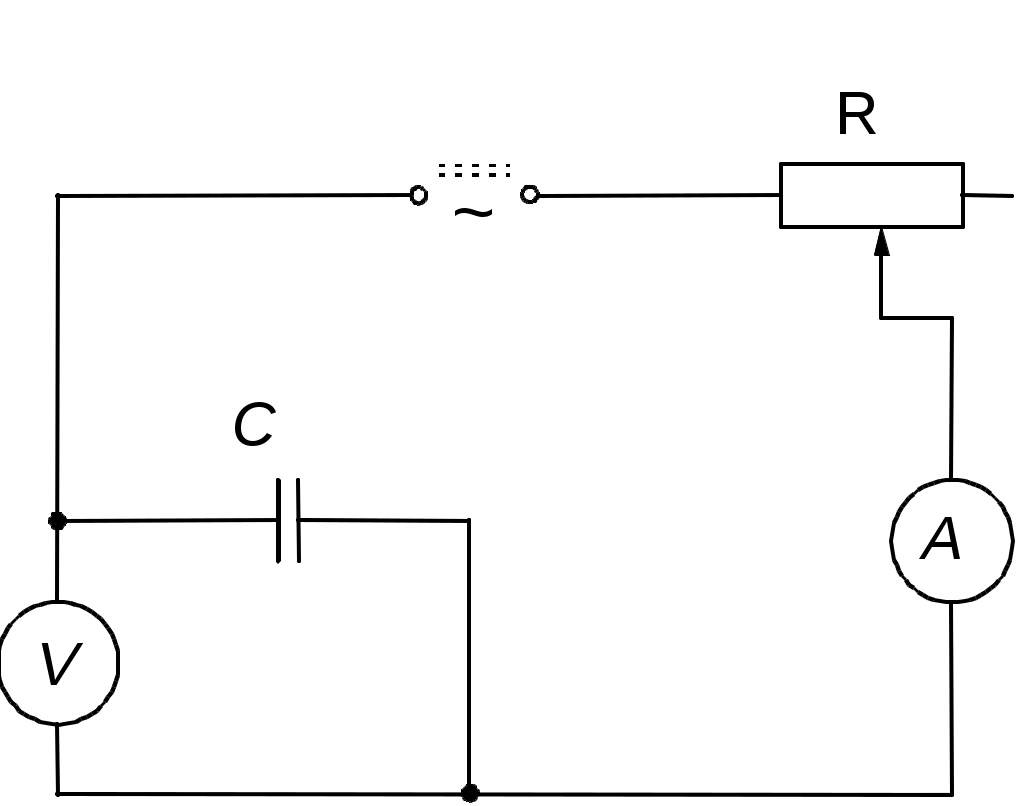
Рис.2.
Для определения Z₂ поступают следующим образом: соединяют последовательно измеряемый конденсатор C, амперметр А и реостат r и подключают их к средним клеммам ключа К (рис.2). Параллельно конденсатору присоединяют вольтметр. Реостат служит здесь лишь предохранителем на случай пробоя или короткого замыкания обкладок конденсатора и должен быть включен на максимальное сопротивление.
Порядок выполнения.

Замыкают ключ на переменный ток и отсчитывают по прибору силу тока I_эфф и напряжение U_эфф. Определив Z₂ по формуле



подставляют это значение Z₂ в формулу (15) и вычисляют С. Измерения производят сначала отдельно для каждого из двух конденсаторов, а затем при параллельном и последовательном их соединении, проверяя тем самым формулы соединений конденсаторов.

Упражнение 3. Проверка полного закона Ома для переменного тока.

Из формулы (11) для случая последовательно включенных сопротивления, индуктивности и ёмкости имеем:

, (16)

. (17)




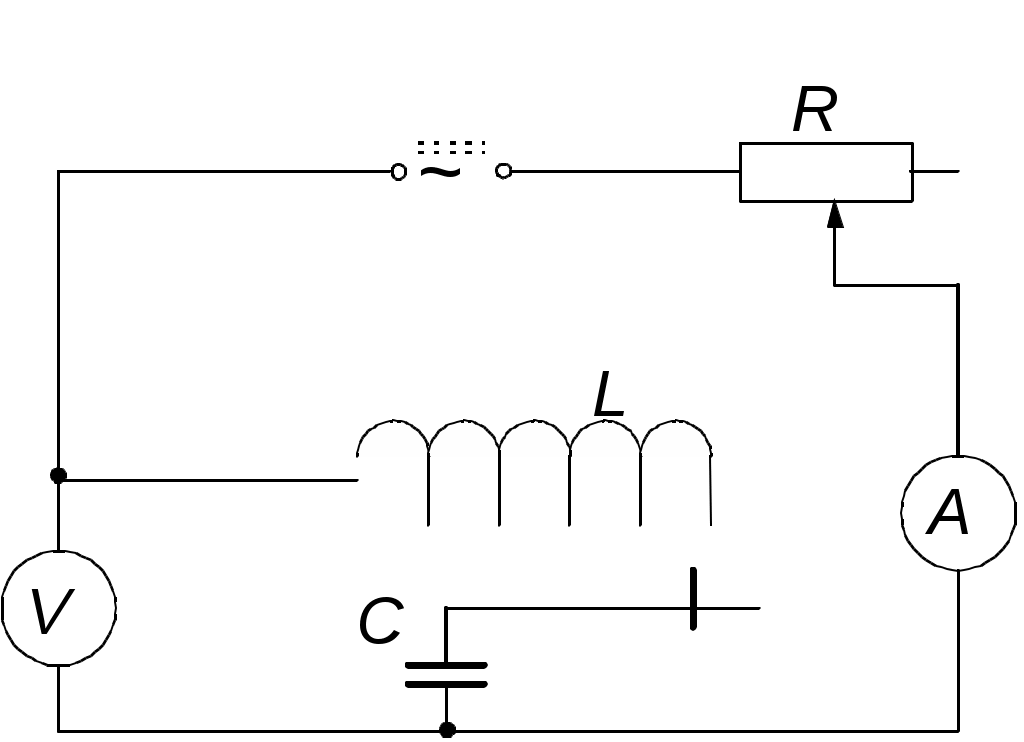
Рис.3.
Для проверки этой формулы в цепь переменного тока включают последовательно: катушку индуктивности с известным активным сопротивлением R и индуктивностью L, конденсатор с известной емкостью С, реостат r и амперметр А (рис.3). Параллельно части цепи, содержащей катушку и конденсатор, подключают вольтметр

---

V.

Порядок выполнения.

Установив реостат на максимум сопротивления, замыкают ключ К на переменный ток. Изменяя затем сопротивление реостата, добиваются достаточных показаний приборов и производят отсчет I_эфф и U_эфф. Полученные результаты подставляют в правую часть формулы (16) и вычисляют R. С другой стороны, значение R определяется из формулы (17) по известным величинам R, L, С.

Полученные результаты сравнивают для проверки справедливости формулы полного закона Ома для переменного тока. Отчет по задаче представляют в виде таблицы измеренных и вычисленных величин сопротивлений участков цепи для переменного тока.

1. 
   
   

---