Файл: Лабораторная работа 38.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 32

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Лабораторная работа № 38


Изучение обобщённого закона Ома
и измерение электродвижущей силы
методом компенсации
Цель работы:

  • изучение зависимости разности потенциалов на участке цепи, содержащем ЭДС, от силы тока;

  • расчёт ЭДС и полного сопротивления данного участка.


Теоретическое введение
Для того чтобы поддерживать движение электрических зарядов в течение некоторого длительного времени, необходимо, кроме электрического поля, наличие в цепи сторонних полей. Сторонние поля действуют на носители тока внутри источников электрической энергии (гальванических элементов, аккумуляторов, электрических генераторов и т.п.).

Для электрического и сторонних полей вводятся силовая и энергетическая характеристики. Силовыми характеристиками являются векторы напряжённости и электрического и сторонних полей соответственно.

Направление вектора напряжённости поля совпадает с направлением соответствующей силы, действующей на положительный заряд. Величина напряжённости численно равна отношению силы к величине заряда:

Энергетической характеристикой электростатического поля является разность потенциалов j1 - j2, стороннего поля – электродвижущая сила E. Величина разности потенциалов равна отношению работы силы электростатического поля Аэл при перемещении малого точечного заряда q из точки 1 участка цепи в точку 2 к величине перемещаемого заряда:

j1 - j2 = .

Величина ЭДС – аналогична отношению работы силы стороннего поля
Астор к величине q:

E = .

Между силовыми и энергетическими характеристиками электростатического и стороннего полей имеются сходные интегральные соотношения:

j1 - j2 = , E = .

Величина, численно равная суммарной работе, совершаемой электростатическими и сторонними силами при перемещении единичного положительного заряда по участку цепи, называется напряжением U на этом участке цепи и равна:


U1-2 = (j1 - j2) + S Ei ,


где знак i – х ЭДС принимается положительным, если направление обхода от точки 1 к точке 2 (рис. 1) соответствует перемещению внутри источника Ei от знака "-" (катод) к знаку "+" (анод). В противном случае – отрицательным. Таким образом, на рис. 1 E1 будет отрицательной, а E2 – положительной.

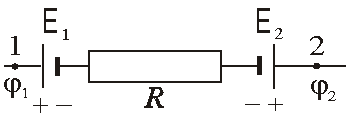Рис. 1
Если использовать определение напряжения U = IRп, где I– сила тока в цепи, Rп – полное сопротивление участка, включающее внутреннее сопротивление источника ЭДС на этом участке, то закон Ома принимает вид:



IRп = (j1 - j2) + S Ei .

(1)



Выражение (1) называют обобщённым законом Ома или законом Ома для неоднородного участка цепи.

Участок цепи, в пределах которого не действуют сторонние силы, называется однородным, напряжение на нём равно U1-2 = j1 - j2, т. е. напряжение совпадает с разностью потенциалов.

За направление электрического тока принимают направление перемещения положительных зарядов. Произведение IRп берётся положительным, если направление тока совпадает с направлением обхода контура.



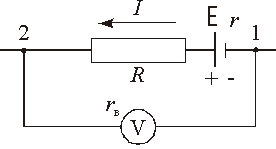Рис. 2
Применим обобщённый закон Ома к участку цепи, изображённому на рис. 2. При решении задач с использованием обобщённого закона Ома направление тока, а также направление обхода контура выбираются произвольно. Выберем условно положительное направление тока, как показано на рисунке, и направление обхода от точки 1 к точке 2. Тогда для участка цепи 1 – E – R – 2 получим:


I(R + r) = (j1 - j2) + E .
(2)


Обобщённый закон Ома, применённый к участку 1 – V – 2 (обход через вольтметр), имеет вид:


Iв rв = j1 - j2,

(3)


где Iв – ток, проходящий через вольтметр, rв – сопротивление вольтметра.

Но произведение Iв rв – это показание вольтметра, следовательно, показание вольтметра, подключенного к концам любого участка цепи, всегда равно разности потенциалов между точками подключения прибора.

Из выражения (2), обозначив полное сопротивление участка
R + r через Rп, получим:


j1 - j2 = IRп - E,

или

j2 - j1 = E - IRп .

(4)


Выражение (4) представляет собой уравнение прямой в координатах (j2 - j1, I), изображённой на рис. 3.

Рис. 3
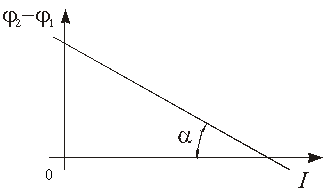Из (4) следует, что если сила тока в цепи равна нулю, то разность потенциалов источника ЭДС, включённого в рассматриваемый участок, j2 - j1 = E, а полное сопротивление участка цепи 1 – 2 равно тангенсу угла a наклона прямой (см. рис. 3):

R = tga .
Описание установки и методики измерений
Схема лабораторной установки приведена на рис. 4.

В состав установки входят:

    • лабораторный модуль;

    • два источника питания ИП1 и ИП2 типа «HY 1802ED», используемых в качестве источников ЭДС «Е1» и «Е2»;

    • два цифровых мультиметра типа «MAS 830B», используемых в качестве измерительных приборов: вольтметра «PV» и миллиамперметра «PA»;

    • два адаптера типа «AC DC», используемых в качестве источников питания измерительных приборов.

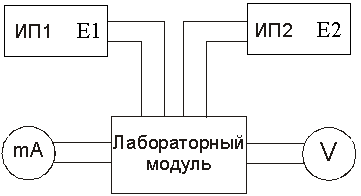Рис. 4






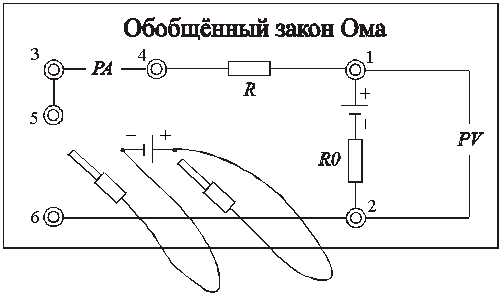Рис. 5


На лицевой панели лабораторного модуля изображена электрическая схема установки (рис. 5) и расположены гнёзда для подключения измерительных приборов. К панели также подведены два гибких вывода, с помощью которых можно подключать с различной полярностью источника питания
«Е1» с ЭДС E1 к исследуемому контуру.

Будем считать, что величина внешней регулируемой ЭДС E1 всегда известна, а постоянная величина E2, создаваемая источником питания «Е2», неизвестна, как и сопротивление участка 1-2. Определим их.

Выберем направление обхода контура от точки 1 к точке 2 (см. рис. 5), а за положительное направление тока примем направление от точки 2 к точке 1, тогда в соответствии с обобщённым законом Ома для участка цепи можно записать

(j1 - j2) – E2 = - IR0 или j1 - j2 = E2 - IR0 ,
(5)

а для замкнутой цепи

I(R + R0) = E2 ± E1.
(6)

Здесь знак "+" будет при согласном включении E2 и E1, а знак "-" при встречном.

Из (6) может быть найдено выражение для величины тока в цепи

.
(7)

Как видно из (7), изменяя величину E1, можно изменять и силу тока. При согласном включении E2 и E1 сила тока I растёт с ростом E1. Из (5) видно, что разность потенциалов j1 - j

Смотрите также файлы