Файл: 1. Аналитические аспекты эффекта Шпольского 3.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 144

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Особенности квазилинейчатых спектров

Квазилинейчатые спектры как метод анализа сложных органических смесей Несмотря на множества преимуществ, проблема происхождения квазилинейчатых спектров в привлекал внимание теоретиков. К.К. Ребане и В.В. Хижнякова, взялись дать теорию квазилинейчатых спектров, учитывая взаимодействие между примесной молекулой и остальным кристаллом[22]. Обычно в кристаллическом состоянии молекулы примеси фиксируются в одинаковых положениях на больших расстояниях друг от друга. Тем самым, отпадает возможность взаимодействия одинаковых близко расположенных молекул, которые могло бы дать размывание спектра за счет слабого снятия вырождений. А так же снимается влияние вращательных степеней свободы, уровни в случае больших молекул расположены настолько близко друг к друг, что они образуют квазиконтинуум.Факт исчезновения большого числа степеней свободы, в момент, когда молекулы сжимаются в кристалле. На самом деле возникает коллективные колебания решетки взамен, трансляционных и вращательных движений, они вовсе исчезают. Для макроскопического кристалла число данных колебаний огромно и, они должны образовывать квазинепрерывную последовательность, так же как в случае вращательных состояний в газе. Явно, что возбуждение примесной молекулы, включенной электронного перехода превратится в колебания решетки. Но в таком случае остается неясным, каким образом спектр кристалла освобождается от размывающего влияния этих колебаний решетки, которое должно бы создавать то же эффект, что квазиконтиннум вращательных состояний в газе. В этой связи Хижняков и Ребане обратили внимание на видимую связь между механизмом возникновения в твердом кристаллическом теле γ-линии с естественной шириной в эффекте Мессбауэра и узких линий в оптическом квазилинейчатом спектре[24]. При испускании γ-квантов часть энергии квантового перехода затрачивается на сообщение излучающему ядру кинетической энергии отдачи. В случае покоящегося свободного ядра энергия излучаемого фотона вследствие этого будет меньше энергии квантового перехода на величину где М - масса ядра. Благодаря этому излучаемая линия должна быть сдвинута относительно линии перехода без отдачи в сторону меньших частот на ту же величину R. Соответственно, при резонансном поглощении, опять-таки в силу закона сохранения импульса, энергии квантового перехода должна быть меньше на ту же величину R, чем энергия падающего фотона. В случае свободных ядер в газе, в след за, этим смещениям присоединяется еще доплеровские смещения вследствие теплового движения ядер источника и поглотителя. В результате кривые излучения и поглощения приобретают нормальный вид и максимумы их оказывается сдвинуты на величину 2R. Если излучающее ядро внедрено в кристаллическую решетку, то импульс отдачи ядра передается соседним атомам, в следствии чего передается часть энергии колебаниям решетки, т. е., иначе говоря, в следствие переходов в ядру рождаются фононы в решетке. Мёссбауэр, показал, что существует конечная вероятность таких переходов, которые не сопровождаются изменением внутреннего состояния кристалла. При этих переходах энергии излучаемого фотона в точности равна энергии квантового перехода в ядре и спектр состоит и невероятно узкой линии, практически с естественной шириной, не осложняемой никакими расширениями.Первоначально данное явление было объяснено просто тем, что в случае таких переходов отдача передается всему кристаллу в целом. И так как масса кристалла имеет огромную величину по сравнению с массой отдельного ядра, передача энергии при этих условиях должна быть пренебрежимо малой. Ввиду этого такие переходы называют обычно переходами без отдачи.Тщательный анализ ситуации показал, что это объяснение точно и существование переходов без изменения внутреннего состояния кристалла (без рождения фононов), когда импульс передается кристаллу целиком, не может быть понятно основе классической механики упругих соударений. На самом деле, безусловно, в момент испускания отдача получает прежде всего излучающее ядро. Эта отдача затем благодаря упругим связям излучающего атома с другими атомами решетки превращается в результате в коллективные колебания кристалла, увеличивая запас его тепловой энергии, т. е. за ней должны следовать фононными переходами. Подобным способом способен произойти, то что данные переходы не окажут влияния на ширину испускаемой γ-линии.Были даже такие предположения, что связи в кристалле настолько сильны, что атом, испытавший отдачу, должен увлечь за собой всю решетку. Но, это оказалось неверным. Элементарный подсчет, сделанный на основании классической динамики соударений, показа, что в среднем решетка получает вследствие отдачи ровно столько же энергии, сколько ее получает свободный атом, т.е.[24]. Это значит, что никакого влияния связей на γ-линию быть не должно так как решетка трактуется классически. На самом деле проблема, эксперимента обнаружившего существование γ-лини «без отдачи», разрешается тем, что проблема является квантовой, а не классической. Поэтому любой эффект связи обнаруживается, когда решетка описывается малыми квантовыми числами, т. е. при низких температурах. Анализ, проведенный Липкина, подводит к выводу, что включение излучающего ядра в кристаллическую решетку создает условия для «излучения без отдачи». Не потому, что ядро замораживается в решетке и не может испытывать отдачу, а главным образом потому, что благодаря связям в кристалле возникают не присутствующие в газ нулевые колебания, создающие предел для передачи энергии решетке[25]. Но так как вследствие правил сумм: Где R —импульс отдачи свободного атома при испускании γ-фотона, , — импульс атома перед испусканием γ-фотона. Скобки означают статистические «моменты»: —первый момент, т. е. математическое ожидание (среднее значение); — второй момент (дисперсия); ρ ( ) характеризует спектр конечного состояния решетки; -энергия начального состояния решетки. Формулы (1) и (2) совпадают с соответствующими формулами, выведенными на основе классической динамики соударений.Площади под кривой распределения энергии в конечном состоянии в случае «газа» и в случае кристалла должны быть одинаковы, это требование удовлетворяется лишь при условии, что в случае кристалла недостающая площадь осуществляется в вид дельта-функции при , которой и соответствует мёссбауэровская линия «без отдачи» (рис. 1). Рис.1. Теория эффекта Мессбауэра.а) Классический спектр газового источника; б) часть прошедшего спектра, соответствующая передаче положительной энергии; в) тот же спектр, что и (б), но с добавлением дельта-финкции[26].Существенно в окончательном выводе то, что испускание в виде широкого квазиконтинума и в виде линии Мёссбауэра суть два независимых процесса, осуществляемых альтернативно, каждый со своей вероятностью. В этом и заключается разгадка отсутствия влияния колебаний решетки на ширину линии без отдачи.Обратив внимание на механизм испускания оптического квазилинейчатого спектра, отчетливо сформулированный Ребане и Хижняков, возникает та же проблема, что и в случае эффекта Мёссбауэра: объяснение того, почему неизбежные коллективные колебания решетки не оказывают влияния на спектр. Речь идет о свойствах спектра, именно: 1) возникновение в твердом кристаллическом теле спектра с линиями, ширина которых порядка немногих обратных сантиметров, вместо наблюдаемых полос шириной в сотни и тысячи обратных сантиметров; 2) строго резонансный характер головной линии (переход 0'—0") спектра.В оптической части спектра импульс отдачи при испускании фотона невероятно мал по сравнению с отдачей при γ-излучении. В следствии возникновение резонанса в излучении и поглощении в оптической части спектра не встречает никаких препятствий в случае свободных молекул (в газе). Но когда молекула включена в кристаллическую решетку, условия изменяются и воздействие кристаллических колебаний должно сказываться на переходе 0'—0", так же как и на ширине линий.Не представляет труда заметить что данную роль, играющий импульс отдачи при испускании γ-фотона, в случае спектра флуоресценции в твердом теле должны играть неизбежные «тепловые» потери, обусловливающие стоксовский сдвиг. Даже в случае если бы эти потери не оказывали влияния на ширину линий, они должны были бы изменить резонанс между головными линиями в спектре поглощения и люминесценции совершенно так же, как импульс отдачи изменяет резонанс в случае γ-флуоресценции. В случае с квазилинейчатыми спектрами совпадение частот линий 0'—0" в поглощении и в эмиссии имеет место всегда и осуществляется в пределах ошибки измерения, т. е. или же, эв. Это свойство квазилинейчатых спектров имеет большое практическое значение, так как именно оно позволяет очень просто выполнять вибрационный анализ электронно-колебательного спектра. По существу, оно, конечно, неотделимо от механизма проявления узких линий, но его наличие с особенной точность показывает, что эффект возникновения квазилинейчатого спектра имеет мало общего с тривиальным эффектом сужения линий вследствие простого понижения температуры.Разберем этот вопрос подробнее и обратимся внимение прежде к случаю неорганических кристаллофосфоров. Выражение стоксовского сдвига в данном случае получило хорошее толкование вследствие применению  так именуемого способа конфигурационной координаты, примененного впервые Ф. Зейтцем. В тех моментах, когда в кристаллофосфоре имеется хорошо локализованный «центр» (простым примером служить щелочно-галоидный кристаллофосфор, активированный ионом таллия ТГ), можно построить модель потенциальных кривых, аналогичную той, какой пользуются в теории двухатомных молекул. Необходимо, однако, иметь в виду существенное различие между обоими случаями. В теории двухатомных молекул потенциальная кривая представляет зависимость потенциальной энергии молекулы от расстояния между ядрами. Вблизи минимума кривая является параболой в соответствии с моделью гармонического осциллятора, и минимум соответствует равновесному расстоянию ядер. В варианте кристаллофосфора кривая являет собой полную энергию решетки в зависимости от некой конфигурационной координаты, характеризующей расположение относительно «центра» соседних атомов (или ионов). Конечно, одной координатой такое расположение охарактеризовать полностью невозможно: необходима была бы самом деле многомерная поверхность. Однако для качественного результата можно пользоваться и одной координатой. Например, в случае превосходного локализованного центра и стремительного уменьшения взаимодействия между «центром» и атомами решетки важную роль играет только передвижение вдоль радиуса-вектора относительно «центра» и конфигурационной координатой может быть расстояние от «центра» до ближайших молекул решетки («дыхательная координата»). Очевидно, что электронное возбуждение «центра» меняет упругие силы взаимодействия между «центром» и решеткой, ввиду чего минимум кривой для возбужденного состояния смещен относительно минимума нижней кривой, как это и показано на рис.2. Рис.2. Схема к методу конфигурационной координаты.При возбуждении «центра» исходя из принципа Франка — Кондона происходит мгновенный переход с нижней кривой на верхнюю кривую по вертикали (АВ), т. е. расстояния между окружением и «центром» сохраняется. По этой причине система оказывается в состоянии с лишней потенциальной энергии, вследствие чего вокруг «центра» возникают колебания, быстро преобразующиеся в нормальные колебания решетки. Через промежуток времени порядка (сек) изображающая точка переходит в минимум верхней кривой, откуда через (сек) происходит переход в D нижней кривой. Здесь также система (центр — окружение) оказывается «нагретой» выше равновесной температуры, возникают колебания, вновь преобразующиеся в нормальные колебания решетки: оптическое поглощение и излучение «центра» сопровождается рождением фононов решетки. Что же касается стоксовского сдвига, то он определяется прямо по чертежу как разность АВ — CD.Число нормальных колебаний (осцилляторов) решетки огромно (оно равно 3N—6, где N — число молекул решетки). Благодаря этому энергия каждого осциллятора квантуется, если передаваемая энергия не слишком мала суперпозиция их будет иметь квазинепрерывную последовательность. Поскольку энергия квантового перехода распределяется между испускаемым фотоном и этим квазинепрерывным спектром колебаний решетки, в результате возникает размытый спектр.С необходимыми изменениями эти соображения могут быть перенесены на интересующий нас случай молекулярного кристалла с включениями в виде более или менее сложных молекул (а не простых ионов, как в неорганических кристаллофосфорах). Вследствие слабости взаимодействий между кристаллом-хозяином и молекулой примеси, молекула примеси находится в хорошо локализованной потенциальной яме. Этот локальный характер в данном случае выражен значительно более совершенным образом, нежели в случае постороннего иона в ионной решетке. Идеальный локальный центр, где внутренние связи во много больше связи с окружающей решеткой-хозяином. Поэтому можно рассматривать независимо друг от друга движение молекулы как целого, описываемое совокупностью координат Q ее центра тяжести, и движение электронов и ядер внутри молекулы, характерно совокупностью их координат q по отношению к центру тяжести. Рассматривая возбуждение молекулы в адиабатическом приближении (т. е. с помощью полуклассического принципа Франка-Кондона на основе обычных молекулярных потенциальных кривых), представление о локальных колебаниях (координаты q), какие есть внутримолекулярные колебания «центра». Они не входят в квазинепрерывный спектр кристалла, и кристалл играет для них роль термостата.Рассматривая движение молекулы, характеризуемое совокупностью координат центра тяжести Q, как целого относительно решетки. Можно повторить сказанное ранее о влиянии колебаний решетки на чисто электронный переход воспользоваться методом конфигурационной координаты. Результатом является размывание электронно-колебательного спектра, идентичный с обычным размыванием примесного электронного спектра в кристаллической среде. Источником этого размывания, является проявление фононов решетки, параллельно электронным переходом в примесной молекуле. И так, обычные электронные переходы в примесной молекуле, не в силах давать узкие и резонансные линия. Данные линии могут возникать только при определенных переходах, которые должны быть бесфононными, в полной аналогии с мёссбауэровскими переходами «без отдачи». Очевидно, в обоих случах мы имеем дело с явлением квантовым, и это именно обстоятельство является причиной необходимости применения низких температур.Возможность «бесфононных» переходов так же «бесфононных» линий была основана различными независимыми путями друг от друга Ребане К. К. и Хижняковым В. В. и Трифоновым Е. Д. Трифонов, проанализировал только математически выражения для вероятности колебательного состояния, которое проявляется в кристалле, когда в примесном центре происходит чисто электронный переход с энергией . В результате интеграл, выражающий плотность вероятности конечного колебательного состояния кристалла, расходится причем эта расходимость тесно связана с б-образной особенностью в точке . Это и доказывает возможность существования при этой частоте «бесфононного» перехода[27]. Хижняков и Ребане детально изучили условия возникновения оптического квазилинейчатого спектра. Вычитав в приближении Франка-Кондона вероятность перехода из исходного состояния кристалла в некоторое другое, когда в примесном центре происходит электронный переход, Хижняков и Ребане анализировали и изучали характер проявляющегося спектра с учетом воздействия осцилляторов решетки. Оказалось, что при всевозможных комбинациях состояний осцилляторов, при переходе между которыми внутреннее состояние кристалла не изменяется. Эти именно переходы между состояниями осцилляторов с идентичными колебательными квантовыми числами: 0—0, 1 — 1, 2—2 и т. д. Поскольку при таких переходах внутреннее состояние кристалла не изменяется, они ведут к возникновению узкой «бесфононной» линии. На самом деле из-за не идеальности кристалла различные примесные дентры находятся в разныхусловиях, что влечет за собой возникновение некоторой статистической ширины. Если между частотами осцилляторов нормального и возбужденного состояний имеется небольшая разница, это может повести к возникновению «сверхтонкой» структуры линии. Таким образом, наблюдаемые бесфононные линии должны быть на самом деле квазилиниями.Во все оставшихся переходах, когда квантовые числа осцилляторов начального и конечного состояний изменяются, должен проявиться размытый спектр. По теории Хижнякова и Ребане, в оптической области в указанных условиях возникает «аддитивный спектр», состоящий из линий и искаженного фона, абсолютно  таким образом же,  равно как это обладает роль в эффекте Мёссбауэра Основной результат своей теории авторы формулируют следующим образом: «Проведенное изучение показывает, что причина появления квазилинейчатых спектров Шпольского, что и возникновения эффекта Мёссбауэра: взаимодействие с колебаниями решетки не уширяет бесфононные линии, а сводится в основном к появлению фона». Хижняков и Ребане сориентировались, таким образом как и  с влиянием температуры в соответствие интенсивностей линий и фона. Оказалось, что с увеличением температуры происходит быстрое перераспределение интенсивности в пользу фона и, обратно, уменьшение температуры ведет к резкому повышению интенсивности линий за счет фона.Данные Ребане и Хижнякова: Проявление сплошного фона (размытой широкой полосы) одновременно с линиями и быстрое убывание интенсивности этого фона при падении температуры. Как правило, при 77° К фон и линии наблюдаются одновременно; при 20° К фон заметно ослабевает, а при 4° К - практически проподает. Возможность существования «сверхтонкой» структуры квазилиний. Обычная ширина линий даже при гелиевых температурах-порядка 1-5 см

2. Объекты и методика исследования2.1. Объекты исследованияВ качестве объектов исследования были выбраны замороженные н.-парафиновые растворы трифенилена и его производных при температуре 77 К. Они относятся к классу полициклических ароматических углеводородов. В таких растворах проявляются квазилинейчатые спектры, также они имеют метастабильный триплетный уровень, который эффективно заселяется при низких температурах [30]. Вследствие собственной геометрии трифенилен и его производные могут образовать микро и наноразмерные структуры. Например, трифенилены, измененные триазолами благодаря алкильным частям, формируют высокоупорядоченные колончатые структуры и высокопористые органогели в смеси циклогексана в твердом состоянии. Такие материалы проявляют высокую селективность к нитроароматическим соединениям в растворе и твердом состоянии [31].Трифенилен и его поли(гетеро)ароматические производные представляют собой интерес также в варианте химических потенциальных сенсоров для соединений полинитроароматических благодаря своим фотолюминесцентным свойствам и способности преобразовывать устойчивые не флуоресцентные π-комплексы с электрон-дефицитными субстратами. При таком взаимодействии производительность тушения фотолюминесценции зависит от скорости переноса электрона от полиароматического соединения (донора) к нитро- соединению акцептору.На основе трифенилена синтезированы соединения, имеющие сенсорные способности для бесконтактного выяснения присутствия нитроароматических соединений на поверхностях, воды в кислороде, в растворах неполярных растворителей, в сверхмалых концентрациях на основании изменения оптических свойств гашения фотолюминесценции. Микроволокна и нановолокна, приобретённые вакуум-возгонкой трифенилена при температуре 150-180 показали отличную селективность к парам нитробензола, что дает возможность для получение простых наноструктурированных материалов [32]. Трифенилен синтезируют из додекагидротрифенилена при обработке катализаторами переходными металлами или действием окислителей. В работе [40] трифенилен был получен при долгом нагревании в течение десяти часов тетрагидротрифенилена с селеном. Синтез трифенилена путем связи на первой стадии циклогексанона последовательно с NaOH, полифосфосфорной кислотой с получением додекагидротрифенилена, который на второй стадии обрабатывают катализатором. Отличающийся применением на первой стадии непрерывной экстракции при выделении додекагидротрифенилена, на второй стадии отличающийся использованием катализатора палладий на сибуните, атмосферы аргона, в ходе реакции с катализатором особо чистый трифенилен помещали на холодную поверхность.Принято считать, что полициклические ароматические углеводороды сравнительно стабильны при ультрафиолетовом облучении. Но за последнее время быстро возросло число работ, посвященных исследованию фотолитической деградации полициклических ароматических углеводородыв в растворах при температуре 77 К. К примеру, в работе M. Lamotte [33] оговаривается о формировании устойчивых люминесцирующих фотопродуктов трифенилена в метилциклогексане при 77 К. Показано, что процесс формирования фотопродукта является двухфотонным, а промежуточное состояние, поглощающее второй фотон, является нижним триплетным состоянием трифенилена. В настоящей работе исследованы фотопревращения молекул трифенилена в системах Шпольского. В качестве объекта был избран раствор трифенилена в различных парафинах при 77 К. Выбор пал на данное вещество потому, что трифенилен из круга соединений предоставляет фотопродукт с сильной флуоресценцией, отличающейся от флуоресценции родительского соединения. Концентрация трифенилена варьировалась в пределах от до М. На рис.3 приведена структурные формулы трифенилена, используемых в экспериментах [34]. Рис. 3. Структурная форма трифенилена (по системе IUPAC – 9,10-БЕНЗФЕНАНТРЕН). Молекулярная формула C18H18.Трифенилен – ангулярный орто-конденсированный углеводород, содержащий два линейно-аннелированных бензольных кольца.В работах [35-37] описаны квазилинейчатые спектры флуоресценции трифенилена. Спектр структурен в н.-гептане и н.-гексане, но в крайнем растворителе немного более резок. Линия 0-0 перехода в н.-гептане – 343,1 нм – ослаблена и объясняется запрещенным характером перехода [36], обусловленная высокой симметрией трифенилена (симметрия молекулы D3h – ось симметрии 3-го порядка).Трифенилен имеет ярко голубую фосфоресценцию большой длительности ( 16,0 с). В работе [38] был впервые получен квазилинейчатый спектр фосфоресценции раствора трифенилена в н.-гексане, затем эти же данные были упомянуты в работе [35]. Кинетика фосфоресценции трифенилена подробно изучена в работах [39, 40], произведены выводы, что при охлаждении до низких температур растворов ароматических углеводородов вследствие чего может проявляться образование микрокристаллов, искажающих спектр и кинетику люминесценции молекул. Наиболее коротковолновая линия спектра фосфоресценции 423,8 нм соответствует 0-0 переходу. Выход фосфоресценции много выше выхода флуоресценции, однако, идентификацию удобнее вести по спектрам фосфоресценции [41]. В работе [42] отмечены некоторые особенности кинетики затухания трифенилена. Двенадцать из них подчиняются строго экспоненциальному закону затухания с характерным временем затухания с. Исследованы двадцать три наиболее интенсивные линии трифенилена. Для пяти квазилиний в коротковолновой части характерно то, что в начале наблюдается более медленное и неэкспоненциальное затухание, которое после нескольких секунд становится экспоненциальным с тем же показателем, как и у остальных квазилиний. У шести квазилиний, находящихся в длинноволновой части спектра наблюдается отклонение от экспоненциального закона в первоначальном периоде затухания. Благодаря результатам авторы сделали вывод, что причиной нарушения экспоненциальности затухания фосфоресценции трифенилена является влияние триплет-триплетного поглощения.Основные люминесцентные характеристики трифенилена при 77 К, а именно время жизни триплетного уровня , частоты, соответствующие синглетным и триплетным переходам, а также полосы триплет-триплетного поглощения приведены в таблицах 1 и 2. Таблица 1.Основные характеристики в различных растворителях

3.2. Методы улучшения структуры спектров

Заключение

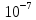с), когда триплетный уровень не заселен, интенсивность флуоресценции достигает максимального значения. Затем за время соизмеримое со временем жизни триплетных молекул она уменьшается и достигает стационарного значения. Этот процесс соответствует переходу части молекул в триплетное состояние.

Интенсивность флуоресценции по мере заселения триплетного уровня уменьшается со временем по экспоненциальному закону. Это уменьшение обусловлено заселением триплетного уровня и насколько эффективно заселяется триплетный уровень, настолько сильно уменьшается интенсивность флуоресценции. Вследствие этого, заселенность триплетного уровня можно рассчитать следующим образом:



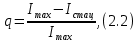
где 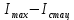характеризует число молекул перешедших в триплетное состояние, 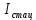– интенсивность флуоресценции в стационарном состоянии, 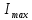– максимальная интенсивность флуоресценции пропорциональная общему числу молекул в растворе, участвующих в излучении.

В том случае, когда триплетный уровень не заселяется или заселяется очень слабо, интенсивность флуоресценции остается постоянной равной 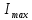и она зависит от интенсивности возбуждения линейно. Регистрацию спектров флуоресценции удобнее вести в стационарном режиме, однако это приводит к неправильному определению интенсивности флуоресценции, так как 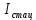зависит от мощности возбуждения. В процессе эксперимента, вследствие нестабильности работы лампы или эффекта внутреннего фильтра, может произойти изменение стационарной интенсивности флуоресценции, а вследствие этого изменение заселенности триплетного уровня молекул. При этом максимальная интенсивность флуоресценции 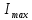будет оставаться постоянной.

Для определения заселенности триплетного уровня трифенилена вторая методика оказалась более удобной. Однако контроль осуществляли с использованием первой методики. Совпадение результатов обеих методик позволило сделать вывод о правомерности использования обеих методик.


При определении относительной заселенности триплетного и синглетного уровней молекул основной вклад в ошибку вносит случайная ошибка, возникающая при измерении времен разгорания и затухания фосфоресценции. Величина погрешности при определении времени разгорания и затухания фосфоресценции в секундном диапазоне обуславливалась флуктуациями фототока, нелинейностью усилителя, погрешностью блока временной развертки и механической постоянной графопостроителя. Три последних источника по данным многократных проверок могли дать в сумме систематическую ошибку не более 1%. Для уменьшения влияния фототока измерения повторялись 5-10 раз и случайная ошибка в каждом конкретном случае находилась с использованием коэффициентов Стьюдента при доверительной вероятности 0,90.

Определенная, с учетом сказанного, абсолютная ошибка при измерении относительной заселенности триплетного уровня молекул равнялась 0,02 единицы.

3. Влияние фотопревращений примесных центров на формирование квазилинейчатых спектров люминесценции

3.1. Фотопреврашения ПАУ в системах Шпольского

Бытует мнение, что полициклические ароматические углеводороды не испытывают фотопревращений при ультрафиолетовом облучении. Но обнаружение и исследование фотохимических превращений ПАУ представляет огромный интерес по нескольким причинам. Во-первых, они могут привести к уменьшению энергии возбуждения, что повлечет за собой переход части упорядоченной энергии электронного возбуждения в неупорядоченную энергию[57]. Во-вторых, реакции фотопревращения можно использоваться для «выжигания» в спектре поглощения замороженных растворов устойчивых провалов[58], распространенный метод для решения ряда задач спектроскопии [59,60]. Одними из первых фотохимические превращения для некоторых ПАУ были обнаружены в ряде работ [61], что говорит о необходимости исследования данного вопроса. Фотопревращения молекул ПАУ могут привести к ошибкам в спектрофлуориметрическом анализе органических соединений по квазилинейчатым спектрам, в том случае, если будет образовываться устойчивый люминесцирующий продукт.

Фотопревращение трифенилена в отвердевшем растворе метилциклогексана впервые было описано в работе. Спектры поглощения и флуоресценции были отнесены к виду дигидротррифенилена, возникающие при внедрении единичной молекулы растворителя к ароматическому углеводороду. Функция создания фотопродукта состоит из поочередного поглощения пары фотонов, однако, при этом нижнее триплетное состояние является промежуточным. Также в работе была определена суммарная эффективность реакции поглощения второго фотона, которая составила примерно
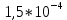на длине волны 265 нм, а в видимой области в 1000 раз меньше ( 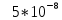), что обусловлено сильным триплетным поглощением в этой области. По словам авторов при ультрафиолетовом облучении ртутной лампой формируется флуоресцирующий фотопродукт. При длительном воздействии на образец возрастает интенсивность свечения фотопродукта. В работе так же указано, что данная реакция не происходит в температурном диапазоне от 19 до 26 (комнатная температура). Следовательно, свойства различны – при низких температурах возрастает время жизни триплетного состояния, возрастает квантовый выход фотореакции, происходящей в данном состоянии, в результате возрастания степени заселенности триплетного уровня молекул за счет увеличения времени жизни. Исходя из работы [62] более подходящими условиями для проявление двухквантовых реакций являются: возрастание интенсивности возбуждающего света и реакционное время жизни. Двухквантовые реакции проще всего производятся в замороженных растворах ароматических молекул в алифатических растворителях так же в полимерных средах, или же просто в жестких средах. Скорость двухквантовой реакции зависит от квадрата интенсивности возбуждающего света.

В настоящей работе было изучено фотопревращение трифенилена в матрицах Шпольского при температуре 77 K (в замороженных твердых растворах). Наиболее «удобным» растворителем считается н.-гептан для получения квазилинейчатых спектров, так же в нем получаются наиболее резкие спектры люминесценции трифенилена, чем в иных растворителях [62]. В противоположность н.-гептану н.-декан является «неудобным» растворителем [62], спектры в н.-декане получаются с широкими полосами. В момент записи спектров люминесценции трифенилена возбуждение осуществлялось азотным лазером ЛГИ-21, интенсивностью ослабленной нейтральным фильтром в 3 раза. На рис. 4 представлен без предварительного облучения спектр люминесценции трифенилена в растворителе н.-гептане при 77 K. Спектр люминесценции трифенилена нормирован по отношению к интенсивности линии 352,87 нм. Расположение линий в спектре и распределение интенсивности в спектре не противоречат литературным данным [63].




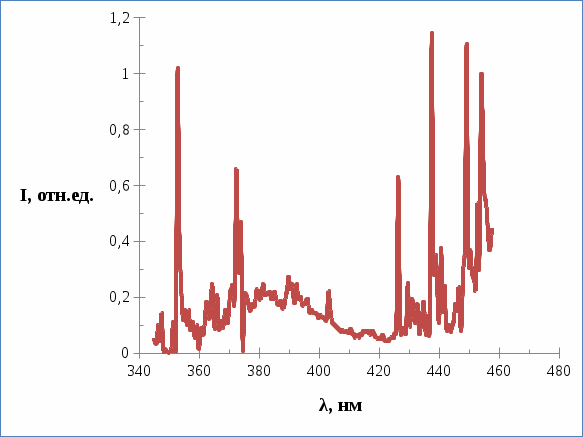
Рис. 4. Спектр люминесценции трифенилена в н.-гептане без предварительного облучения.

Далее исследуемый образец облучался азотным лазером ЛГИ-21 без уменьшения интенсивности в течение 10 минут и снова записывался спектр люминесценции трифенилена, который представлен на рис. 5.



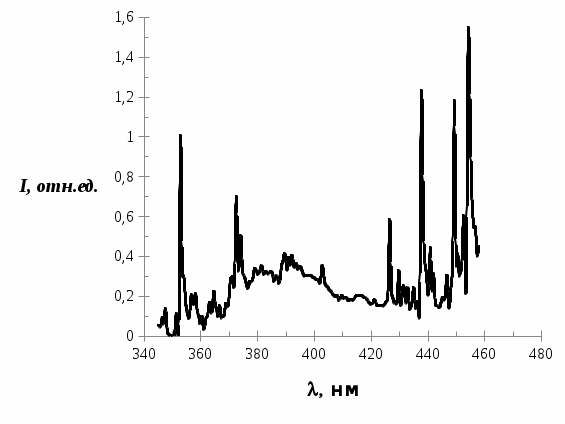
Рис. 5. Спектр люминесценции трифенилена в н.-гептане после облучения в течение 10 минут.

Как видно, в спектре люминесценции трифенилена в области от 360 нм до 420 нм проявляется дополнительное свечение, которое отсутствует в случае образца без облучения. Интенсивность дополнительного свечения возрастает со временем и достигает некого значения.

Дальнейшее облучение образца вплоть до 90 минут привело, к тому что в спектре трифенилена появилось очень сильное свечение, возрастающее со временем, которое можно увидеть на рисунках 6-8.



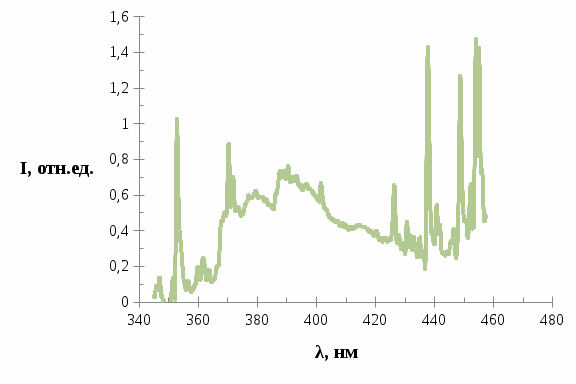
Рис. 6. Спектр люминесценции трифенилена в н.-гептане после облучения в течение 30 минут.



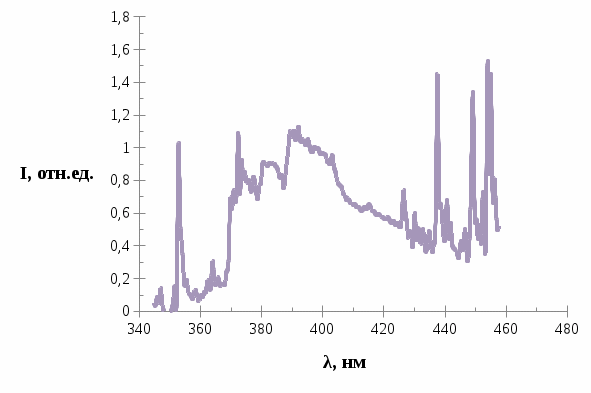
Рис. 7. Спектр люминесценции трифенилена в н.-гептане после облучения в течение 60 минут.

Спектры на рис.4, рис.5, рис.6, рис.7, рис.8 приведены для концентрации трифенилена в растворе 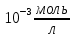. В спектре проявляются широкие полосы с максимумами в области 370, 380 и 390 нм.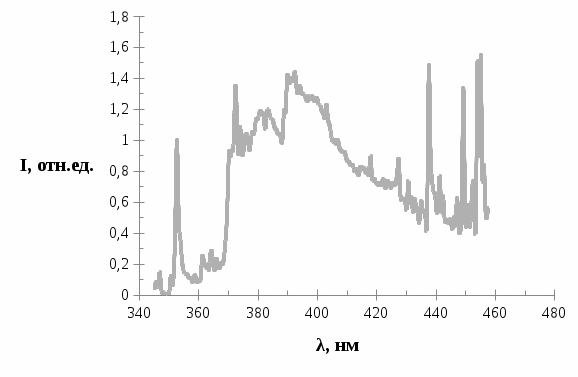



Рис. 8. Спектр люминесценции трифенилена в н.-гептане после облучения в течение 90 минут.

Полученный нами фотопродукт по свои параметрам (распределением интенсивности в спектре и положением полос) совпадает с параметрами спектра фотопродукта трифенилена в метилциклогексане при 77 K [33] При сравнении рис.4 (первоначальный спектр) и рис.8 (при облучении лазером на протяжении полутора часов) видно, что возрастает свечение фотопродукта в 5-6 раз, при этом происходит уменьшение интенсивности фосфоресценции трифенилена всего на 5-10%. Снижение интенсивности квазилинейчатого спектра фосфоресценции трифенилена говорит о том, что за фотопревращение в данном случае, ответственны внедренные молекулы в кристаллы н.-парафина, то есть молекулы трифенилена.

С целью проверки не является ли свечение фотопродукта итогом фотопревращения примесей трифенилена или растворителя (так же воды и кислорода) было выполнено фракционирование трифенилена с помощью хроматографической колонки. В результате фракционирования было выявлено семь фракций. В доказательство теории о вероятности проявления фотопродукта обусловлено фотопревращением трифенилена, а никак не присутствием в составе образца примесей, люминесценция фотопродукта прослеживается только лишь в тех фракциях, в каких присутствует трифенилен.


На рис.9 представлен график, демонстрирующий повышение фотопродукта трифенилена с увеличение времени при облучении лазером ЛГИ-21. Как видно, прослеживается существенное увеличение свечения фотопродукта, который с ходом времени ощущает истощение.

Рассмотрим кинетику изменения числа молекул фотопродукта со временим. Пусть 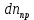– изменение числа молекул фотопродукта за время dt, тогда с течением времени это число изменяется по закону:

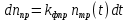(3.1)

где 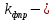константа фотопревращения, которая характеризует вероятность превращения молекул трифенилена поcле поглощения второго кванта, 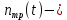число молекул трифенилена в растворе.

В начальный момент времени изменение числа молекул фотопродукта было равно 0:



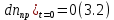
Из одной молекулы трифенилена может образоваться одна молекула фотопродукта, тогда:



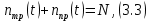
где N число молекул трифенилена до начала реакции.

Подставляя (3.3) в (3.1) получим дифференциальное уравнение, показывающие изменение числа молекул фотопродукта со временем:



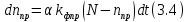
Здесь α коэффициент, который определяет долю молекул трифенилена, находящихся в триплетном состоянии. Решая это уравнение, получим: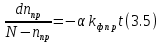



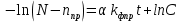(3.6)

С учетом начальных условий, С=N, тогда:



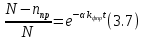
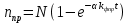(3.8)

Выражение (3.8) справедливо для части молекул трифенилена, которая учувствует в фотореакции. Поскольку интенсивность линий в квазилинейчатых спектрах пропорциональна числу молекул, тогда для интенсивности можно записать:

Смотрите также файлы