Добавлен: 23.11.2023
Просмотров: 145
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(3.9)
или
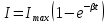 , (3.10)
, (3.10)
где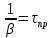 – время жизни молекул фотопродукта.
– время жизни молекул фотопродукта.
Рассмотрим кинетику изменения числа молекул трифенилена.
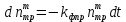 (3.11)
(3.11)
где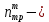 число молекул трифенилена в триплетном состоянии.
число молекул трифенилена в триплетном состоянии.
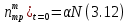
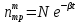 (3.13)
(3.13)
Тогда интенсивность фосфоресценции трифенилена будет определяться выражением:
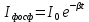 (3.14)
(3.14)
или
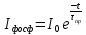 (3.15)
(3.15)
Для всех молекул трифенилена, получим:
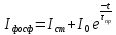 (3.16)
(3.16)
где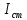 – стационарная интенсивность,
– стационарная интенсивность, 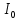 – начальная интенсивность, при этом
– начальная интенсивность, при этом 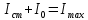 .
.
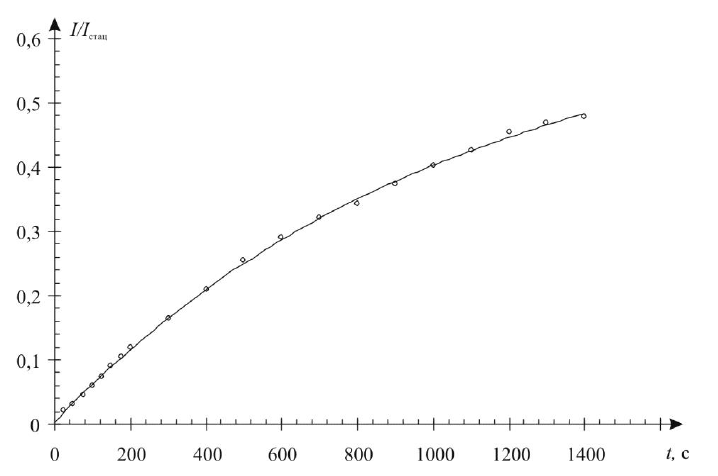
Рис. 9. Кинетика накопления фотопродукта трифенилена в н.-гептане при облучении лазером.
Оказалось, что скорость и интенсивность люминесценции образования фотопродукта существенно зависят от способа возбуждения. Наибольшая интенсивность свечения фотопродукта и скорость его накопления наблюдается при возбуждении лазером ЛГИ-21. При использовании дуговой ксеноновой шаровой лампы сверхвысокого давления ДКсШ-150 с фильтром 313 нм образование фотопродукта было существенно меньшим и нарастание его было не таким очевидным.
Насыщение фотореакции при лазерном возбуждении может быть вызвано двумя причинами. Первая – в силу каких-либо причин лишь часть молекул трифенилена, которая участвует в излучении, испытывает фотопревращение. Вторая – с наступлением динамического равновесия в случае, когда фотореакция обратима.
Если бы насыщение было обусловлено наступлением динамического равновесия между прямым и обратным процессами, то после прекращения возбуждения и выдержки образца в течение некоторого времени в темноте интенсивность люминесценции фотопродукта должна была бы уменьшиться. Однако выдерживание образца в темноте в течение времени, равного времени, после которого наступает насыщение интенсивность флуоресценции фотопродукта не изменяется. Это говорит о том, что обратная реакция отсутствует, из этого следует вывод о том, что наступление насыщения фотореакции не связано с наступлением динамического равновесия.
Больше всего подходит к результатам эксперимента предположения о том, что в случае насыщения фотореакции не все молекулы трифенилена участвуют в нем. Причины такой избирательности по отношению к превращению могут быть следующими. Нижнее триплетное состояние является, поглощающим вторым фотоном в промежуточном состоянии, то в фотопревращении будут участвовать только те молекулы, для которых разности энергий первого и второго триплетных состояний равна энергия квантов падающего излучения. Данное условие выполняется не для всех молекул, исключение служит монохроматическая подставка в триплетную полосу. Если в ширину полос триплет-триплетного поглощения существенный вклад вносит неоднородное уширение, то в фотореакции будут участвовать только часть молекул трифенилена, для которых монохроматическое излучение резонансно с триплет-триплетным поглощением[64]. Следовательно, с течением времени накопление фотопродукта прекращается, если лазерное возбуждение попадает в резонанс с триплет-триплетным поглощением для небольшого числа молекул. В момент ослабление интенсивности возбуждения в 3 раза интенсивность излучения фотопродукта стремительно спадает, что приводит к снижению его выхода. Затухание люминесценции получаемого фотопродукта происходит за время, меньшего 1 мкс, что указывает на флуоресцентный характер свечения.
Исследование показало, что при облучении лазером ЛГИ-21 в н.-парафиновых растворах трифенилена при 77 K в спектральной области 360-420 нм появляется излучение, приписываемое нами излучению фотопродукта. Таким образом, результаты исследований показали, что фотопревращение с образованием люминесцирующего фотопродукта могут испытывать центры, ответственные за квазилинейчатые спектры в системах Шпольского. Этот факт необходимо учитывать при анализе сложных органических смесей по квазилинейчатым спектрам люминесценции по следующим причинам. Во-первых, люминесценция фотопродукта усложняет анализ спектра, во-вторых, в результате фотопревращения происходит уменьшение концентрации исходного вещества и в-третьих, фотопродукт может интенсивно поглощать возбуждающий свет, в результате чего возбуждение отдельных компонент сложной смеси ослабляется, что способно послужить причиной к перераспределению интенсивности в спектре многокомпонентных смесей ПАУ.
Bибрационный анализ спектра фосфоресценции трифенилена в предположении, что частота наиболее коротковолновой линии соответствует 0-0 переходу, был выполнен в работе Д.М. Гребенщикова и В.А. Бутлара [36]. Однако, точно установить 0-0 переход им не удалось. Это вызвано следующими причинами: во-первых, в области 0-0 перехода спектра наблюдаются линии, относящиеся к спектру фосфоресценции примеси, которую было трудно отделить от основного вещества, во-вторых, в результате высокой симметрии молекулы трифенилена (см. рис. 3) линия в спектре фосфоресценции соответствующая 0-0 переходу очень слабая.
Соответствие размера и формы молекулы трифенилена и примеси, не позволяют методу жидкостной хроматографии полностью избавиться от примеси.
Если предположить, что наблюдаемая линия в спектре соответствует 0-0 переходу, тогда следует, увеличение интенсивности примеси относительно других линий обусловлено более низкой симметрией молекулы примеси, а первый триплетный уровень примеси несколько смещен относительно соответствующего уровня трифенилена.
Согласно предположению о соответствии размеров молекулы трифенилена и молекулы примеси, примесью является какая-то производная трифенилена. Были изучены имеющиеся в литературе спектры фосфоресценции следующих производных трифенилена: 1-азатрифенилена [65, 66, 67], 1,4-диазатрифенилена [65, 67], 1,3,5- трифенилбензола [68].
При очистке трифенилена было выделено 7 фракций. Наиболее интенсивные линии в спектре фосфоресценции раствора примеси в н.-гексане приведены в таблице 3. В этой же таблице приведены результаты измерений длин волн квазилиний спектра фосфоресценции примеси и длины волн 1-азатрифенилена, взятые из работы[66]. Есть хорошее соответствие длин волн, и распределение интенсивностей в квазилинейчатых спектрах примеси и 1-азатрифенилена.
Симметрия молекулы 1-азатрифенилена ниже, чем молекулы трифенилена, что согласуется с усилением линии, соответствующей линии 0-0 перехода для 1-азатрифенилена в сравнении с линией 0-0 перехода трифенилена.
В отсутствие реабсорбции излучения и дополнительных каналов дезактивации энергии триплетного возбуждения затухание фосфоресценции происходит по экспоненциальному закону. На рис. 10 представлена кривая затухания фосфоресценции фотопродукта по линии, соответствующей длине волны λ=
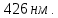
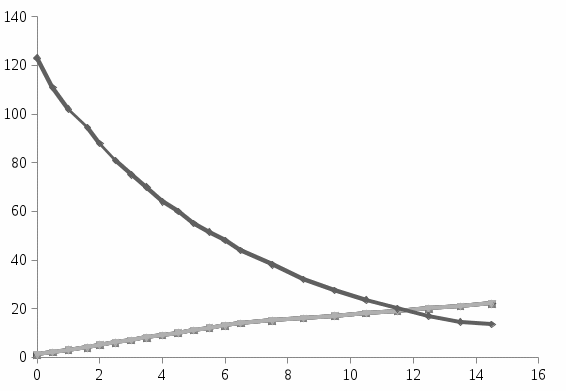
Рис. 10. Затухание фосфоресценции фотопродукта.
Для определения времени жизни триплетного состояния был построен этот график в полулогарифмическом масштабе (рис.11), из анализа полученного графика было определено время жизни триплетного состояния, которое составило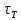 =6,5±0,2 с исходя из уравнения y = -0,154x - 0,023, что в пределах ошибки измерения совпадает с временем жизни триплетного состояния 1-азатрифенилена в том же растворителе
=6,5±0,2 с исходя из уравнения y = -0,154x - 0,023, что в пределах ошибки измерения совпадает с временем жизни триплетного состояния 1-азатрифенилена в том же растворителе 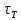 =6,5 с [65].
=6,5 с [65].
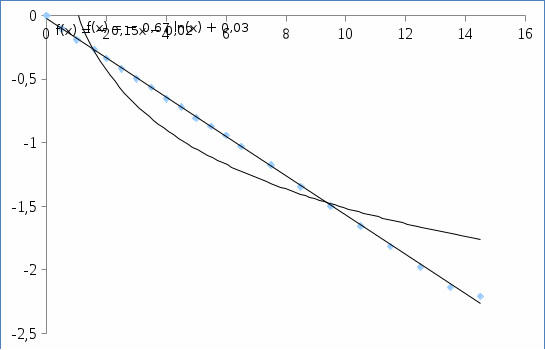
Рис. 11. К определению времени жизни триплетного состояния примеси трифенилена.
Сравнение спектров фосфоресценции примеси трифенилена и
1-азатрифенилена.
Примечание: о. и. – очень интенсивная, и. – интенсивная, ср. – средняя, сл. слабая.
Спектр фосфоресценции примеси, соответственно и кинетика совпадают с кинетикой и спектром 1-азатрифенилена в тех же условиях, что позволяет сделать вывод о том, что примесью в трифенилене является 1-азатрифенилен. Поскольку внедренные молекулы могут испытывать фотопревращение, была исследована возможность фотопревращения 1-азатрифенилена. Для этого образец 1-азатрифенилена облучался излучением азотного лазера в течение определенного отрезка времени. Следующим шагом фиксировались линия в спектре фосфоресценции 1-азатрифенилена, соответствующая 0-0 переходу. По изменению пиковой интенсивности указанной линии судили об изменении концентрации 1-азатрифенилена в раствора. Характерное время процесса фотопревращения примеси составляло 66 минут. С целью контроля считается ли реакция обратимой или нет, образец уже после облучения выдерживался в темноте в течение часа. Отсутствие изменений в интенсивности фосфоресценции указывают на необратимость фотореакции.
Таким образом, при взаимодействии лазерного излучения происходит необратимое фотопревращение 1-азатрифенилена. Продукты фотореакции не люминесцируют в видимой области. При этом хотя трифенилен так же подвергается фоторазложению, доля его молекул, участвующих в реакции столь незначительна, что изменение в интенсивности фосфоресценции за время неоратимого фотохимического превращения вещества, следовательно и уменьшение концентрации вещества и уменьшение интенсивности излучение вещества, примеси практически не наблюдается.
Молекулы трифенилена, ответственные за квазилинейчатые спектры фосфоресценции так же испытывают фотопревращение. Люминесцирующий фотопродукт образуется в результате такого фотопревращения, спектр которого не зависит от природы растворителя и совпадает со спектром фотопродукта, который наблюдали авторы [33] в метилциклогексане. Как и в метилциклогексане в н.-парафиновых растворах фотореакция является двухквантовой. Промежуточным состоянием, с участием которого происходит поглощение второго кванта, является нижнее триплетное состояние. Поэтому эффективность протекания такой фотореакции существенным образом зависит от заселенности триплетного уровня молекул, ответственных за квазилинейчатый спектр люминесценции.
или
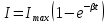 , (3.10)
, (3.10)где
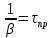 – время жизни молекул фотопродукта.
– время жизни молекул фотопродукта.Рассмотрим кинетику изменения числа молекул трифенилена.
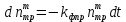 (3.11)
(3.11)где
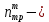 число молекул трифенилена в триплетном состоянии.
число молекул трифенилена в триплетном состоянии. 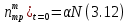
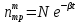 (3.13)
(3.13)Тогда интенсивность фосфоресценции трифенилена будет определяться выражением:
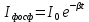 (3.14)
(3.14)или
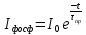 (3.15)
(3.15)Для всех молекул трифенилена, получим:
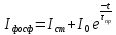 (3.16)
(3.16)где
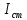 – стационарная интенсивность,
– стационарная интенсивность, 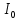 – начальная интенсивность, при этом
– начальная интенсивность, при этом 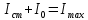 .
.
Рис. 9. Кинетика накопления фотопродукта трифенилена в н.-гептане при облучении лазером.
Оказалось, что скорость и интенсивность люминесценции образования фотопродукта существенно зависят от способа возбуждения. Наибольшая интенсивность свечения фотопродукта и скорость его накопления наблюдается при возбуждении лазером ЛГИ-21. При использовании дуговой ксеноновой шаровой лампы сверхвысокого давления ДКсШ-150 с фильтром 313 нм образование фотопродукта было существенно меньшим и нарастание его было не таким очевидным.
Насыщение фотореакции при лазерном возбуждении может быть вызвано двумя причинами. Первая – в силу каких-либо причин лишь часть молекул трифенилена, которая участвует в излучении, испытывает фотопревращение. Вторая – с наступлением динамического равновесия в случае, когда фотореакция обратима.
Если бы насыщение было обусловлено наступлением динамического равновесия между прямым и обратным процессами, то после прекращения возбуждения и выдержки образца в течение некоторого времени в темноте интенсивность люминесценции фотопродукта должна была бы уменьшиться. Однако выдерживание образца в темноте в течение времени, равного времени, после которого наступает насыщение интенсивность флуоресценции фотопродукта не изменяется. Это говорит о том, что обратная реакция отсутствует, из этого следует вывод о том, что наступление насыщения фотореакции не связано с наступлением динамического равновесия.
Больше всего подходит к результатам эксперимента предположения о том, что в случае насыщения фотореакции не все молекулы трифенилена участвуют в нем. Причины такой избирательности по отношению к превращению могут быть следующими. Нижнее триплетное состояние является, поглощающим вторым фотоном в промежуточном состоянии, то в фотопревращении будут участвовать только те молекулы, для которых разности энергий первого и второго триплетных состояний равна энергия квантов падающего излучения. Данное условие выполняется не для всех молекул, исключение служит монохроматическая подставка в триплетную полосу. Если в ширину полос триплет-триплетного поглощения существенный вклад вносит неоднородное уширение, то в фотореакции будут участвовать только часть молекул трифенилена, для которых монохроматическое излучение резонансно с триплет-триплетным поглощением[64]. Следовательно, с течением времени накопление фотопродукта прекращается, если лазерное возбуждение попадает в резонанс с триплет-триплетным поглощением для небольшого числа молекул. В момент ослабление интенсивности возбуждения в 3 раза интенсивность излучения фотопродукта стремительно спадает, что приводит к снижению его выхода. Затухание люминесценции получаемого фотопродукта происходит за время, меньшего 1 мкс, что указывает на флуоресцентный характер свечения.
Исследование показало, что при облучении лазером ЛГИ-21 в н.-парафиновых растворах трифенилена при 77 K в спектральной области 360-420 нм появляется излучение, приписываемое нами излучению фотопродукта. Таким образом, результаты исследований показали, что фотопревращение с образованием люминесцирующего фотопродукта могут испытывать центры, ответственные за квазилинейчатые спектры в системах Шпольского. Этот факт необходимо учитывать при анализе сложных органических смесей по квазилинейчатым спектрам люминесценции по следующим причинам. Во-первых, люминесценция фотопродукта усложняет анализ спектра, во-вторых, в результате фотопревращения происходит уменьшение концентрации исходного вещества и в-третьих, фотопродукт может интенсивно поглощать возбуждающий свет, в результате чего возбуждение отдельных компонент сложной смеси ослабляется, что способно послужить причиной к перераспределению интенсивности в спектре многокомпонентных смесей ПАУ.
3.2. Методы улучшения структуры спектров
Bибрационный анализ спектра фосфоресценции трифенилена в предположении, что частота наиболее коротковолновой линии соответствует 0-0 переходу, был выполнен в работе Д.М. Гребенщикова и В.А. Бутлара [36]. Однако, точно установить 0-0 переход им не удалось. Это вызвано следующими причинами: во-первых, в области 0-0 перехода спектра наблюдаются линии, относящиеся к спектру фосфоресценции примеси, которую было трудно отделить от основного вещества, во-вторых, в результате высокой симметрии молекулы трифенилена (см. рис. 3) линия в спектре фосфоресценции соответствующая 0-0 переходу очень слабая.
Соответствие размера и формы молекулы трифенилена и примеси, не позволяют методу жидкостной хроматографии полностью избавиться от примеси.
Если предположить, что наблюдаемая линия в спектре соответствует 0-0 переходу, тогда следует, увеличение интенсивности примеси относительно других линий обусловлено более низкой симметрией молекулы примеси, а первый триплетный уровень примеси несколько смещен относительно соответствующего уровня трифенилена.
Согласно предположению о соответствии размеров молекулы трифенилена и молекулы примеси, примесью является какая-то производная трифенилена. Были изучены имеющиеся в литературе спектры фосфоресценции следующих производных трифенилена: 1-азатрифенилена [65, 66, 67], 1,4-диазатрифенилена [65, 67], 1,3,5- трифенилбензола [68].
При очистке трифенилена было выделено 7 фракций. Наиболее интенсивные линии в спектре фосфоресценции раствора примеси в н.-гексане приведены в таблице 3. В этой же таблице приведены результаты измерений длин волн квазилиний спектра фосфоресценции примеси и длины волн 1-азатрифенилена, взятые из работы[66]. Есть хорошее соответствие длин волн, и распределение интенсивностей в квазилинейчатых спектрах примеси и 1-азатрифенилена.
Симметрия молекулы 1-азатрифенилена ниже, чем молекулы трифенилена, что согласуется с усилением линии, соответствующей линии 0-0 перехода для 1-азатрифенилена в сравнении с линией 0-0 перехода трифенилена.
В отсутствие реабсорбции излучения и дополнительных каналов дезактивации энергии триплетного возбуждения затухание фосфоресценции происходит по экспоненциальному закону. На рис. 10 представлена кривая затухания фосфоресценции фотопродукта по линии, соответствующей длине волны λ=
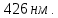

Рис. 10. Затухание фосфоресценции фотопродукта.
Для определения времени жизни триплетного состояния был построен этот график в полулогарифмическом масштабе (рис.11), из анализа полученного графика было определено время жизни триплетного состояния, которое составило
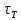 =6,5±0,2 с исходя из уравнения y = -0,154x - 0,023, что в пределах ошибки измерения совпадает с временем жизни триплетного состояния 1-азатрифенилена в том же растворителе
=6,5±0,2 с исходя из уравнения y = -0,154x - 0,023, что в пределах ошибки измерения совпадает с временем жизни триплетного состояния 1-азатрифенилена в том же растворителе 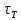 =6,5 с [65].
=6,5 с [65]. 
Рис. 11. К определению времени жизни триплетного состояния примеси трифенилена.
Сравнение спектров фосфоресценции примеси трифенилена и
| | Линии спектра фосфоресценции примеси | Линии спектра фосфоресценции 1-азатрифенилена [66] |
1-азатрифенилена.
| № | λ, нм | Интенсивность | λ, нм | Интенсивность |
| 1 | 426,6 | о. о. и. | 426,4 | о. О. и. |
| 2 | 434,4 | и. | 434,2 | И. |
| 3 | 437,3 | ср.и. | 437,1 | ср.и. |
| 4 | 439,6 | сл.и. | 439,4 | сл.и. |
| 5 | 441,4 | ср.сл.и. | 441,2 | ср.сл.и. |
| 6 | 445,6 | ср.сл.и. | 445,4 | ср.сл.и. |
| 7 | 451,3 | ср.и. | 451,1 | ср.и. |
| 8 | 452,5 | и. | 452,3 | И. |
| 9 | 454,7 | ср.и. | 454,5 | ср.сл.и. |
| 10 | 458,1 | о.и. | 457,9 | о.и. |
Примечание: о. и. – очень интенсивная, и. – интенсивная, ср. – средняя, сл. слабая.
Спектр фосфоресценции примеси, соответственно и кинетика совпадают с кинетикой и спектром 1-азатрифенилена в тех же условиях, что позволяет сделать вывод о том, что примесью в трифенилене является 1-азатрифенилен. Поскольку внедренные молекулы могут испытывать фотопревращение, была исследована возможность фотопревращения 1-азатрифенилена. Для этого образец 1-азатрифенилена облучался излучением азотного лазера в течение определенного отрезка времени. Следующим шагом фиксировались линия в спектре фосфоресценции 1-азатрифенилена, соответствующая 0-0 переходу. По изменению пиковой интенсивности указанной линии судили об изменении концентрации 1-азатрифенилена в раствора. Характерное время процесса фотопревращения примеси составляло 66 минут. С целью контроля считается ли реакция обратимой или нет, образец уже после облучения выдерживался в темноте в течение часа. Отсутствие изменений в интенсивности фосфоресценции указывают на необратимость фотореакции.
Таким образом, при взаимодействии лазерного излучения происходит необратимое фотопревращение 1-азатрифенилена. Продукты фотореакции не люминесцируют в видимой области. При этом хотя трифенилен так же подвергается фоторазложению, доля его молекул, участвующих в реакции столь незначительна, что изменение в интенсивности фосфоресценции за время неоратимого фотохимического превращения вещества, следовательно и уменьшение концентрации вещества и уменьшение интенсивности излучение вещества, примеси практически не наблюдается.
Молекулы трифенилена, ответственные за квазилинейчатые спектры фосфоресценции так же испытывают фотопревращение. Люминесцирующий фотопродукт образуется в результате такого фотопревращения, спектр которого не зависит от природы растворителя и совпадает со спектром фотопродукта, который наблюдали авторы [33] в метилциклогексане. Как и в метилциклогексане в н.-парафиновых растворах фотореакция является двухквантовой. Промежуточным состоянием, с участием которого происходит поглощение второго кванта, является нижнее триплетное состояние. Поэтому эффективность протекания такой фотореакции существенным образом зависит от заселенности триплетного уровня молекул, ответственных за квазилинейчатый спектр люминесценции.