Файл: 1. Аналитические аспекты эффекта Шпольского 3.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Реферат

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 148

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

Особенности квазилинейчатых спектров

Квазилинейчатые спектры как метод анализа сложных органических смесей Несмотря на множества преимуществ, проблема происхождения квазилинейчатых спектров в привлекал внимание теоретиков. К.К. Ребане и В.В. Хижнякова, взялись дать теорию квазилинейчатых спектров, учитывая взаимодействие между примесной молекулой и остальным кристаллом[22]. Обычно в кристаллическом состоянии молекулы примеси фиксируются в одинаковых положениях на больших расстояниях друг от друга. Тем самым, отпадает возможность взаимодействия одинаковых близко расположенных молекул, которые могло бы дать размывание спектра за счет слабого снятия вырождений. А так же снимается влияние вращательных степеней свободы, уровни в случае больших молекул расположены настолько близко друг к друг, что они образуют квазиконтинуум.Факт исчезновения большого числа степеней свободы, в момент, когда молекулы сжимаются в кристалле. На самом деле возникает коллективные колебания решетки взамен, трансляционных и вращательных движений, они вовсе исчезают. Для макроскопического кристалла число данных колебаний огромно и, они должны образовывать квазинепрерывную последовательность, так же как в случае вращательных состояний в газе. Явно, что возбуждение примесной молекулы, включенной электронного перехода превратится в колебания решетки. Но в таком случае остается неясным, каким образом спектр кристалла освобождается от размывающего влияния этих колебаний решетки, которое должно бы создавать то же эффект, что квазиконтиннум вращательных состояний в газе. В этой связи Хижняков и Ребане обратили внимание на видимую связь между механизмом возникновения в твердом кристаллическом теле γ-линии с естественной шириной в эффекте Мессбауэра и узких линий в оптическом квазилинейчатом спектре[24]. При испускании γ-квантов часть энергии квантового перехода затрачивается на сообщение излучающему ядру кинетической энергии отдачи. В случае покоящегося свободного ядра энергия излучаемого фотона вследствие этого будет меньше энергии квантового перехода на величину где М - масса ядра. Благодаря этому излучаемая линия должна быть сдвинута относительно линии перехода без отдачи в сторону меньших частот на ту же величину R. Соответственно, при резонансном поглощении, опять-таки в силу закона сохранения импульса, энергии квантового перехода должна быть меньше на ту же величину R, чем энергия падающего фотона. В случае свободных ядер в газе, в след за, этим смещениям присоединяется еще доплеровские смещения вследствие теплового движения ядер источника и поглотителя. В результате кривые излучения и поглощения приобретают нормальный вид и максимумы их оказывается сдвинуты на величину 2R. Если излучающее ядро внедрено в кристаллическую решетку, то импульс отдачи ядра передается соседним атомам, в следствии чего передается часть энергии колебаниям решетки, т. е., иначе говоря, в следствие переходов в ядру рождаются фононы в решетке. Мёссбауэр, показал, что существует конечная вероятность таких переходов, которые не сопровождаются изменением внутреннего состояния кристалла. При этих переходах энергии излучаемого фотона в точности равна энергии квантового перехода в ядре и спектр состоит и невероятно узкой линии, практически с естественной шириной, не осложняемой никакими расширениями.Первоначально данное явление было объяснено просто тем, что в случае таких переходов отдача передается всему кристаллу в целом. И так как масса кристалла имеет огромную величину по сравнению с массой отдельного ядра, передача энергии при этих условиях должна быть пренебрежимо малой. Ввиду этого такие переходы называют обычно переходами без отдачи.Тщательный анализ ситуации показал, что это объяснение точно и существование переходов без изменения внутреннего состояния кристалла (без рождения фононов), когда импульс передается кристаллу целиком, не может быть понятно основе классической механики упругих соударений. На самом деле, безусловно, в момент испускания отдача получает прежде всего излучающее ядро. Эта отдача затем благодаря упругим связям излучающего атома с другими атомами решетки превращается в результате в коллективные колебания кристалла, увеличивая запас его тепловой энергии, т. е. за ней должны следовать фононными переходами. Подобным способом способен произойти, то что данные переходы не окажут влияния на ширину испускаемой γ-линии.Были даже такие предположения, что связи в кристалле настолько сильны, что атом, испытавший отдачу, должен увлечь за собой всю решетку. Но, это оказалось неверным. Элементарный подсчет, сделанный на основании классической динамики соударений, показа, что в среднем решетка получает вследствие отдачи ровно столько же энергии, сколько ее получает свободный атом, т.е.[24]. Это значит, что никакого влияния связей на γ-линию быть не должно так как решетка трактуется классически. На самом деле проблема, эксперимента обнаружившего существование γ-лини «без отдачи», разрешается тем, что проблема является квантовой, а не классической. Поэтому любой эффект связи обнаруживается, когда решетка описывается малыми квантовыми числами, т. е. при низких температурах. Анализ, проведенный Липкина, подводит к выводу, что включение излучающего ядра в кристаллическую решетку создает условия для «излучения без отдачи». Не потому, что ядро замораживается в решетке и не может испытывать отдачу, а главным образом потому, что благодаря связям в кристалле возникают не присутствующие в газ нулевые колебания, создающие предел для передачи энергии решетке[25]. Но так как вследствие правил сумм: Где R —импульс отдачи свободного атома при испускании γ-фотона, , — импульс атома перед испусканием γ-фотона. Скобки означают статистические «моменты»: —первый момент, т. е. математическое ожидание (среднее значение); — второй момент (дисперсия); ρ ( ) характеризует спектр конечного состояния решетки; -энергия начального состояния решетки. Формулы (1) и (2) совпадают с соответствующими формулами, выведенными на основе классической динамики соударений.Площади под кривой распределения энергии в конечном состоянии в случае «газа» и в случае кристалла должны быть одинаковы, это требование удовлетворяется лишь при условии, что в случае кристалла недостающая площадь осуществляется в вид дельта-функции при , которой и соответствует мёссбауэровская линия «без отдачи» (рис. 1). Рис.1. Теория эффекта Мессбауэра.а) Классический спектр газового источника; б) часть прошедшего спектра, соответствующая передаче положительной энергии; в) тот же спектр, что и (б), но с добавлением дельта-финкции[26].Существенно в окончательном выводе то, что испускание в виде широкого квазиконтинума и в виде линии Мёссбауэра суть два независимых процесса, осуществляемых альтернативно, каждый со своей вероятностью. В этом и заключается разгадка отсутствия влияния колебаний решетки на ширину линии без отдачи.Обратив внимание на механизм испускания оптического квазилинейчатого спектра, отчетливо сформулированный Ребане и Хижняков, возникает та же проблема, что и в случае эффекта Мёссбауэра: объяснение того, почему неизбежные коллективные колебания решетки не оказывают влияния на спектр. Речь идет о свойствах спектра, именно: 1) возникновение в твердом кристаллическом теле спектра с линиями, ширина которых порядка немногих обратных сантиметров, вместо наблюдаемых полос шириной в сотни и тысячи обратных сантиметров; 2) строго резонансный характер головной линии (переход 0'—0") спектра.В оптической части спектра импульс отдачи при испускании фотона невероятно мал по сравнению с отдачей при γ-излучении. В следствии возникновение резонанса в излучении и поглощении в оптической части спектра не встречает никаких препятствий в случае свободных молекул (в газе). Но когда молекула включена в кристаллическую решетку, условия изменяются и воздействие кристаллических колебаний должно сказываться на переходе 0'—0", так же как и на ширине линий.Не представляет труда заметить что данную роль, играющий импульс отдачи при испускании γ-фотона, в случае спектра флуоресценции в твердом теле должны играть неизбежные «тепловые» потери, обусловливающие стоксовский сдвиг. Даже в случае если бы эти потери не оказывали влияния на ширину линий, они должны были бы изменить резонанс между головными линиями в спектре поглощения и люминесценции совершенно так же, как импульс отдачи изменяет резонанс в случае γ-флуоресценции. В случае с квазилинейчатыми спектрами совпадение частот линий 0'—0" в поглощении и в эмиссии имеет место всегда и осуществляется в пределах ошибки измерения, т. е. или же, эв. Это свойство квазилинейчатых спектров имеет большое практическое значение, так как именно оно позволяет очень просто выполнять вибрационный анализ электронно-колебательного спектра. По существу, оно, конечно, неотделимо от механизма проявления узких линий, но его наличие с особенной точность показывает, что эффект возникновения квазилинейчатого спектра имеет мало общего с тривиальным эффектом сужения линий вследствие простого понижения температуры.Разберем этот вопрос подробнее и обратимся внимение прежде к случаю неорганических кристаллофосфоров. Выражение стоксовского сдвига в данном случае получило хорошее толкование вследствие применению  так именуемого способа конфигурационной координаты, примененного впервые Ф. Зейтцем. В тех моментах, когда в кристаллофосфоре имеется хорошо локализованный «центр» (простым примером служить щелочно-галоидный кристаллофосфор, активированный ионом таллия ТГ), можно построить модель потенциальных кривых, аналогичную той, какой пользуются в теории двухатомных молекул. Необходимо, однако, иметь в виду существенное различие между обоими случаями. В теории двухатомных молекул потенциальная кривая представляет зависимость потенциальной энергии молекулы от расстояния между ядрами. Вблизи минимума кривая является параболой в соответствии с моделью гармонического осциллятора, и минимум соответствует равновесному расстоянию ядер. В варианте кристаллофосфора кривая являет собой полную энергию решетки в зависимости от некой конфигурационной координаты, характеризующей расположение относительно «центра» соседних атомов (или ионов). Конечно, одной координатой такое расположение охарактеризовать полностью невозможно: необходима была бы самом деле многомерная поверхность. Однако для качественного результата можно пользоваться и одной координатой. Например, в случае превосходного локализованного центра и стремительного уменьшения взаимодействия между «центром» и атомами решетки важную роль играет только передвижение вдоль радиуса-вектора относительно «центра» и конфигурационной координатой может быть расстояние от «центра» до ближайших молекул решетки («дыхательная координата»). Очевидно, что электронное возбуждение «центра» меняет упругие силы взаимодействия между «центром» и решеткой, ввиду чего минимум кривой для возбужденного состояния смещен относительно минимума нижней кривой, как это и показано на рис.2. Рис.2. Схема к методу конфигурационной координаты.При возбуждении «центра» исходя из принципа Франка — Кондона происходит мгновенный переход с нижней кривой на верхнюю кривую по вертикали (АВ), т. е. расстояния между окружением и «центром» сохраняется. По этой причине система оказывается в состоянии с лишней потенциальной энергии, вследствие чего вокруг «центра» возникают колебания, быстро преобразующиеся в нормальные колебания решетки. Через промежуток времени порядка (сек) изображающая точка переходит в минимум верхней кривой, откуда через (сек) происходит переход в D нижней кривой. Здесь также система (центр — окружение) оказывается «нагретой» выше равновесной температуры, возникают колебания, вновь преобразующиеся в нормальные колебания решетки: оптическое поглощение и излучение «центра» сопровождается рождением фононов решетки. Что же касается стоксовского сдвига, то он определяется прямо по чертежу как разность АВ — CD.Число нормальных колебаний (осцилляторов) решетки огромно (оно равно 3N—6, где N — число молекул решетки). Благодаря этому энергия каждого осциллятора квантуется, если передаваемая энергия не слишком мала суперпозиция их будет иметь квазинепрерывную последовательность. Поскольку энергия квантового перехода распределяется между испускаемым фотоном и этим квазинепрерывным спектром колебаний решетки, в результате возникает размытый спектр.С необходимыми изменениями эти соображения могут быть перенесены на интересующий нас случай молекулярного кристалла с включениями в виде более или менее сложных молекул (а не простых ионов, как в неорганических кристаллофосфорах). Вследствие слабости взаимодействий между кристаллом-хозяином и молекулой примеси, молекула примеси находится в хорошо локализованной потенциальной яме. Этот локальный характер в данном случае выражен значительно более совершенным образом, нежели в случае постороннего иона в ионной решетке. Идеальный локальный центр, где внутренние связи во много больше связи с окружающей решеткой-хозяином. Поэтому можно рассматривать независимо друг от друга движение молекулы как целого, описываемое совокупностью координат Q ее центра тяжести, и движение электронов и ядер внутри молекулы, характерно совокупностью их координат q по отношению к центру тяжести. Рассматривая возбуждение молекулы в адиабатическом приближении (т. е. с помощью полуклассического принципа Франка-Кондона на основе обычных молекулярных потенциальных кривых), представление о локальных колебаниях (координаты q), какие есть внутримолекулярные колебания «центра». Они не входят в квазинепрерывный спектр кристалла, и кристалл играет для них роль термостата.Рассматривая движение молекулы, характеризуемое совокупностью координат центра тяжести Q, как целого относительно решетки. Можно повторить сказанное ранее о влиянии колебаний решетки на чисто электронный переход воспользоваться методом конфигурационной координаты. Результатом является размывание электронно-колебательного спектра, идентичный с обычным размыванием примесного электронного спектра в кристаллической среде. Источником этого размывания, является проявление фононов решетки, параллельно электронным переходом в примесной молекуле. И так, обычные электронные переходы в примесной молекуле, не в силах давать узкие и резонансные линия. Данные линии могут возникать только при определенных переходах, которые должны быть бесфононными, в полной аналогии с мёссбауэровскими переходами «без отдачи». Очевидно, в обоих случах мы имеем дело с явлением квантовым, и это именно обстоятельство является причиной необходимости применения низких температур.Возможность «бесфононных» переходов так же «бесфононных» линий была основана различными независимыми путями друг от друга Ребане К. К. и Хижняковым В. В. и Трифоновым Е. Д. Трифонов, проанализировал только математически выражения для вероятности колебательного состояния, которое проявляется в кристалле, когда в примесном центре происходит чисто электронный переход с энергией . В результате интеграл, выражающий плотность вероятности конечного колебательного состояния кристалла, расходится причем эта расходимость тесно связана с б-образной особенностью в точке . Это и доказывает возможность существования при этой частоте «бесфононного» перехода[27]. Хижняков и Ребане детально изучили условия возникновения оптического квазилинейчатого спектра. Вычитав в приближении Франка-Кондона вероятность перехода из исходного состояния кристалла в некоторое другое, когда в примесном центре происходит электронный переход, Хижняков и Ребане анализировали и изучали характер проявляющегося спектра с учетом воздействия осцилляторов решетки. Оказалось, что при всевозможных комбинациях состояний осцилляторов, при переходе между которыми внутреннее состояние кристалла не изменяется. Эти именно переходы между состояниями осцилляторов с идентичными колебательными квантовыми числами: 0—0, 1 — 1, 2—2 и т. д. Поскольку при таких переходах внутреннее состояние кристалла не изменяется, они ведут к возникновению узкой «бесфононной» линии. На самом деле из-за не идеальности кристалла различные примесные дентры находятся в разныхусловиях, что влечет за собой возникновение некоторой статистической ширины. Если между частотами осцилляторов нормального и возбужденного состояний имеется небольшая разница, это может повести к возникновению «сверхтонкой» структуры линии. Таким образом, наблюдаемые бесфононные линии должны быть на самом деле квазилиниями.Во все оставшихся переходах, когда квантовые числа осцилляторов начального и конечного состояний изменяются, должен проявиться размытый спектр. По теории Хижнякова и Ребане, в оптической области в указанных условиях возникает «аддитивный спектр», состоящий из линий и искаженного фона, абсолютно  таким образом же,  равно как это обладает роль в эффекте Мёссбауэра Основной результат своей теории авторы формулируют следующим образом: «Проведенное изучение показывает, что причина появления квазилинейчатых спектров Шпольского, что и возникновения эффекта Мёссбауэра: взаимодействие с колебаниями решетки не уширяет бесфононные линии, а сводится в основном к появлению фона». Хижняков и Ребане сориентировались, таким образом как и  с влиянием температуры в соответствие интенсивностей линий и фона. Оказалось, что с увеличением температуры происходит быстрое перераспределение интенсивности в пользу фона и, обратно, уменьшение температуры ведет к резкому повышению интенсивности линий за счет фона.Данные Ребане и Хижнякова: Проявление сплошного фона (размытой широкой полосы) одновременно с линиями и быстрое убывание интенсивности этого фона при падении температуры. Как правило, при 77° К фон и линии наблюдаются одновременно; при 20° К фон заметно ослабевает, а при 4° К - практически проподает. Возможность существования «сверхтонкой» структуры квазилиний. Обычная ширина линий даже при гелиевых температурах-порядка 1-5 см

2. Объекты и методика исследования2.1. Объекты исследованияВ качестве объектов исследования были выбраны замороженные н.-парафиновые растворы трифенилена и его производных при температуре 77 К. Они относятся к классу полициклических ароматических углеводородов. В таких растворах проявляются квазилинейчатые спектры, также они имеют метастабильный триплетный уровень, который эффективно заселяется при низких температурах [30]. Вследствие собственной геометрии трифенилен и его производные могут образовать микро и наноразмерные структуры. Например, трифенилены, измененные триазолами благодаря алкильным частям, формируют высокоупорядоченные колончатые структуры и высокопористые органогели в смеси циклогексана в твердом состоянии. Такие материалы проявляют высокую селективность к нитроароматическим соединениям в растворе и твердом состоянии [31].Трифенилен и его поли(гетеро)ароматические производные представляют собой интерес также в варианте химических потенциальных сенсоров для соединений полинитроароматических благодаря своим фотолюминесцентным свойствам и способности преобразовывать устойчивые не флуоресцентные π-комплексы с электрон-дефицитными субстратами. При таком взаимодействии производительность тушения фотолюминесценции зависит от скорости переноса электрона от полиароматического соединения (донора) к нитро- соединению акцептору.На основе трифенилена синтезированы соединения, имеющие сенсорные способности для бесконтактного выяснения присутствия нитроароматических соединений на поверхностях, воды в кислороде, в растворах неполярных растворителей, в сверхмалых концентрациях на основании изменения оптических свойств гашения фотолюминесценции. Микроволокна и нановолокна, приобретённые вакуум-возгонкой трифенилена при температуре 150-180 показали отличную селективность к парам нитробензола, что дает возможность для получение простых наноструктурированных материалов [32]. Трифенилен синтезируют из додекагидротрифенилена при обработке катализаторами переходными металлами или действием окислителей. В работе [40] трифенилен был получен при долгом нагревании в течение десяти часов тетрагидротрифенилена с селеном. Синтез трифенилена путем связи на первой стадии циклогексанона последовательно с NaOH, полифосфосфорной кислотой с получением додекагидротрифенилена, который на второй стадии обрабатывают катализатором. Отличающийся применением на первой стадии непрерывной экстракции при выделении додекагидротрифенилена, на второй стадии отличающийся использованием катализатора палладий на сибуните, атмосферы аргона, в ходе реакции с катализатором особо чистый трифенилен помещали на холодную поверхность.Принято считать, что полициклические ароматические углеводороды сравнительно стабильны при ультрафиолетовом облучении. Но за последнее время быстро возросло число работ, посвященных исследованию фотолитической деградации полициклических ароматических углеводородыв в растворах при температуре 77 К. К примеру, в работе M. Lamotte [33] оговаривается о формировании устойчивых люминесцирующих фотопродуктов трифенилена в метилциклогексане при 77 К. Показано, что процесс формирования фотопродукта является двухфотонным, а промежуточное состояние, поглощающее второй фотон, является нижним триплетным состоянием трифенилена. В настоящей работе исследованы фотопревращения молекул трифенилена в системах Шпольского. В качестве объекта был избран раствор трифенилена в различных парафинах при 77 К. Выбор пал на данное вещество потому, что трифенилен из круга соединений предоставляет фотопродукт с сильной флуоресценцией, отличающейся от флуоресценции родительского соединения. Концентрация трифенилена варьировалась в пределах от до М. На рис.3 приведена структурные формулы трифенилена, используемых в экспериментах [34]. Рис. 3. Структурная форма трифенилена (по системе IUPAC – 9,10-БЕНЗФЕНАНТРЕН). Молекулярная формула C18H18.Трифенилен – ангулярный орто-конденсированный углеводород, содержащий два линейно-аннелированных бензольных кольца.В работах [35-37] описаны квазилинейчатые спектры флуоресценции трифенилена. Спектр структурен в н.-гептане и н.-гексане, но в крайнем растворителе немного более резок. Линия 0-0 перехода в н.-гептане – 343,1 нм – ослаблена и объясняется запрещенным характером перехода [36], обусловленная высокой симметрией трифенилена (симметрия молекулы D3h – ось симметрии 3-го порядка).Трифенилен имеет ярко голубую фосфоресценцию большой длительности ( 16,0 с). В работе [38] был впервые получен квазилинейчатый спектр фосфоресценции раствора трифенилена в н.-гексане, затем эти же данные были упомянуты в работе [35]. Кинетика фосфоресценции трифенилена подробно изучена в работах [39, 40], произведены выводы, что при охлаждении до низких температур растворов ароматических углеводородов вследствие чего может проявляться образование микрокристаллов, искажающих спектр и кинетику люминесценции молекул. Наиболее коротковолновая линия спектра фосфоресценции 423,8 нм соответствует 0-0 переходу. Выход фосфоресценции много выше выхода флуоресценции, однако, идентификацию удобнее вести по спектрам фосфоресценции [41]. В работе [42] отмечены некоторые особенности кинетики затухания трифенилена. Двенадцать из них подчиняются строго экспоненциальному закону затухания с характерным временем затухания с. Исследованы двадцать три наиболее интенсивные линии трифенилена. Для пяти квазилиний в коротковолновой части характерно то, что в начале наблюдается более медленное и неэкспоненциальное затухание, которое после нескольких секунд становится экспоненциальным с тем же показателем, как и у остальных квазилиний. У шести квазилиний, находящихся в длинноволновой части спектра наблюдается отклонение от экспоненциального закона в первоначальном периоде затухания. Благодаря результатам авторы сделали вывод, что причиной нарушения экспоненциальности затухания фосфоресценции трифенилена является влияние триплет-триплетного поглощения.Основные люминесцентные характеристики трифенилена при 77 К, а именно время жизни триплетного уровня , частоты, соответствующие синглетным и триплетным переходам, а также полосы триплет-триплетного поглощения приведены в таблицах 1 и 2. Таблица 1.Основные характеристики в различных растворителях

3.2. Методы улучшения структуры спектров

Заключение

Особенности квазилинейчатых спектров


В работах Прихотько А.Ф. и Шпака М.Т. в показано, когда мощное электронно-фононные взаимодействия ведут к разрушению энергетических уровней, так одинокие полосы притягиваются в широкую линию, она сохраняет целостность вплоть до низких температур при заморозке. В случае нормальных ароматических углеводородов толона а так же и стильбена, при изучении в виде чистых кристаллов они сохраняют целостность вдоль до 20 К.

Необычные спектры постоянно проявляются в сложных веществах в кристаллическом состоянии. Данные спектры характерны тем, что решены схожести со спектром поглощения и много перемещается в красную часть спектра, кристаллическом состоянии спектр флуоресценции целиком теряет структуру, так как в растворах при небольших концентрациях спектры поглощения и люминесценции обладают некой структурой и вероятно выполняют правило зеркальной симметрии. Отметим что данные спектры относят к «резонансным димерам», появившимся в момент возбужденного состояния, в то время как схожие переходы зависят от переноса электрона.

Сокращение расстояния меж излучающими молекулами обязано привести к большому сокращению размывания спектра или же уменьшить вероятность появления аномального спектра. Если же, останется тоже самое положение молекул во всей кристаллической решетки или, первоначальное количество избранных положений (перпендикулярных), то вероятней всего проявится неискаженный либо слабо искаженный спектр. Подобную ситуацию можно воспроизвести, внедрив поглощающие либо же излучающие молекулы в чужеродную кристаллическую решетку, которая должна подходить по требованиям. Перечислим требования, к которым должна удовлетворять кристаллическая решетка. Во-первых, должно иметь слабую связь с молекулами излучения. Во-вторых, матрица должна быть жесткой, так как молекулы должны внедряться без деформации, и молекула должна быть ограничена в свободе, для фиксации в строгом положении. В-третьих, кристаллическая решетка должна иметь прозрачные свойства в точках внедренных молекул. Конечно, найти подходящие матрицы индивидуально для каждой молекулы трудно, но в случае удачи, вероятнее всего, молекулы образуют систему, для которой применима модель «ориентированного газа».

Легче всего воспроизвести данные условия ориентированного газа способом изоморфного обмена между определенными молекулами кристалла-растворителя и молекулами исследуемого нами вещества. По причини условий изоморфизма, матрица и активатор должны иметь схожесть по составу, по структуре и химическими свойствам соответствовать требованиям представлению о изоморфизме. Cидманом и Мак-Клюром было установлено экспериментальное удовлетворение требованием изоморфизма, а так же условия ориентированного газа в смешанных кристаллах ароматических углеводородов, для двух-трех пар вещества, в том числе дурол (симметричный тетраметилбензол) с внедренным в него нафталином. Во предыдущих случаях было установлено, что в подходящей обстановке внедренные молекулы действительно ведут себя как ориентированный газ и, выдают близкие к линейчатым спектрам. Явно видно, что в случаях, когда установлена задача изучения спектра молекул в состояниях, а механизм молекулярного поглощения света кристаллом (представляет большой интерес), данный метод смешанных кристаллов имеет огромное преобладание перед изучением чистых кристаллов. Большие ограничения несет за собой
использование в роли кристалла-хозяина вещества, вещество принадлежащие к одному и тому же классу соединений, что и исследуемое вещество. И так, выше перечисленные условия и требования сводят число вероятно подходящих пар веществ к единичным случаям. И все единичные пары веществ должны подчиняться двум жестким условиям: во-первых, кристаллическая решетка растворителя должны быть прозрачна во всей области, во-вторых, требования изоморфизма.

Более точна экспериментальная сводка фактов, данных и теоретических соображений об изоморфизме в связи со строении атомов и молекул, принадлежит Гримму и Вольфу[14]. Данная сводка, основыноым образом основана на данных на материале неорганических соединений; сводка прекрасно раскрывает преобладающую часть сложности явлений даже в сфере неорганических веществ, где условия порядком проще чем в случае органических веществ. Для простоты восприятия сформулированы два условия изоморфизма в «узком» и «широком» смысле.

В случае «изоморфизма в узком смысле слова», по Гримму, «Способность образования смешанных кристаллов определяется следующими тремя условиями:

  1. химическое строение должно быть одинаково;

  2. кристаллическая решетка должна быть одинакова;

  3. атомные или ионные расстояния в кристалле должны быть близкими; требуемая степень близости зависит от температуры и типа связи».

В работах Мак-Клюра и Сидмана, а также Прихотько и Шпака удовлетворялись все три условия «изоморфизма в узком смысле» по Гримму. При органических соединениях, вероятность формирование примесных кристаллов вероятнее, гораздо более широких, нежели сформулированные Гриммом условия «изоморфизма в широком смысле».

Метод парафиновых растворов при низких температурах отличается простотой и эффективностью. Способы использования методы получения линейчатых спектров, весьма огромны, так как кристаллические парафины предоставляют матрицы с весьма большим набором размеров молекул. В таком случае «структурные спектры», но и аномальные спектры, проявляющиеся исключительно в кристаллическом состоянии континуум, разлагающиеся на спектры, в составе которых сотни линий «атомной» ширины[15].

Когда вероятность получения методом линейчатых спектров широкого спектра веществ была доказана, необходимо было подтвердить, что данные спектры точно относятся к молекулам активаторов. Определение из состава спектра колебательных частот для определенного числа молекул, таких как бензол, нафталин, и т.д., для них колебательные частоты, даны из анализа колебательных спектров (инфракрасных и рамановских). Данная работа была проведена в лабораториях профессоров Пастейля и профессоров Руссе и Бордо а так же Болотниковой Т.Н. Все профессора обнаружили невероятное совпадение частот, обоими направлениями. Это предоставляет не возможность применение спектров произведенных данным способом для определения колебательных частот нормального состояния, так же подтверждает что в системах присутствует «замороженный газ».


Таким образом производился анализ колебательных частот круга сложных органических соединений, относящихся к различным классам: полициклические конденсированные ароматические углеводороды, полиеновые и полифенильные цепочки, некоторые красители, ароматические альдегиды и кетоны и некие другие классы. Невероятными преобладанием этого метода над другими является, простота, малое количества вещества, нужное для проявления спектра (примерно 1 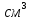, а в случае необходимой концентрации кюветы вероятно меньше), большая точность, способность определения одновременно высоких частот, и малых частот.

Теперь о происхождении квазилинейчатых спектров. Назревает вопрос: почему данные нормальные парафины имеют столь невероятными свойствами с точки зрения спектроскопии. Одну из главный ролей имеет полная оптическая прозрачность вплоть до далекого ультрафиолетового диапазона, важную роль играет еще и химическая инертностью парафинов. Из рассмотренных выше работ видно, получаемые спектры порядком сильней размыты, нежели спектры в парафиновых матрицах при той же температуре, и в условиях изучения спектров веществ (а так жебензола) в матрицах замороженных благородных газов (А, Kr, Хе) при 4,2 K[16].

В матрицах благородных газов спектры бензола проявляют большй сдвиг (до 500 ) в различных матрицах. Абсолютно никакого схожего эффекта не присутствует в случае парафиновых матриц. Это и объясняет, что сечения низких температур с инертностью и прозрачностью нормальных парафинов мало для разъяснения великолепной резкости квазилинейчатых спектров так и сложных органических веществ.

Для подробного разбора механизма происхождения квазилинейчатых спектров, нужно знать присутствуют, ли внедренные молекулы вещества при низкой температуре в парафиновой матрице в молекулярно-дисперсном состоянии и не проявляет ли себе оно (случае плохой растворимости) при замораживании в виде каких-либо агрегатов или даже микрокристалликов? Ответ на данный вопрос дается самим характером спектра люминесценции: буквально все рассматриваемые вещества дают спектр флуоресценции в кристаллическом состоянии практически до самых низких температур в виде указанного прежде континуума, на много сдвинутого длинноволновую сторону в отличие от дискретных линейчатых спектров, видимых парафиновых растворах при низкой температуре. Следовательно, что вещество (активатор) находится в парафиновой матрице в виде молекулярно-дисперсного твердого раствора. В данной ситуации нужно рассмотреть, какие характеристики молекулярной структуры нормальных парафинов которые дают возможность образование твердого раствора ароматического углеводорода, несмотря на отсутствие условий изоморфизма между растворителем и растворенным веществом.


Состоянии активаторов парафиновой матрице наиболее простые в том случае, когда активатором является молекула ароматического углеводорода с конденсированным «линейным» расположением бензольных ядер (нафталин, антрацен, нафтацен). Одно из требований «изоморфизма в широком смысле» (по Гримму), а именно схожесть размеров молекул активатора и матрицы - для этих систем приветствуется. В случае проявления линейчатого спектра с более узкими линиями, присутствует отличное согласие с одной стороны, от парафина, который дает превосходные условия для возникновения линейчатого спектра, с другой стороны, между размерами длинных осей молекул ароматики.

Спектр пентана улучшается по отношению к спектрам нафталина в гексане и в гептане из-за меньшей свободы геометрического расположения молекул. Если же размеры молекул матрицы меньше размеров молекулы активатора, то улучшение спектра, явно, связано с искажением молекулы активатора. Например, имеется идентичное совпадение размеров молекул спектра гексана, со спектром антрацена в пентане, полосы которого размыты.

Несмотря на немалую разницу в кристаллической решетке, в структуре молекул и в их химических составах между молекулами ароматики и парафина имеются более глубокие черты соответствия. Структурный анализ линейной ароматики (нафталин, антрацен) обнаружил Робертсон, что и в этом случае размеры осей a и b остаются одинаковыми, а ось с увеличивается так же, как и у парафинов, на 2,5 А с прибавлением каждого нового бензольного кольца ароматики. И так, между молекулами активатора и матрицы в тех случаях, когда квазилинейчатые спектры имеют наивысшее разрешение, является не только приближенное равенство длин, но и геометрическое подобие зигзагов «синморфизм».

Подобные формы могут сыграть ощутимую роль в формировании твердых растворов замещения, во-первых, синморфиз играет важную роль в формировании смешанного кристалла, так как он полезен при осуществлении основного принципа органической кристаллохимии - принципа «плотнейшей упаковки» о А. И. Китайгородский[17]. Во-вторых, это подтверждают работы Джузеппе Бруни, так же [18]. Джузеппе Бруни, лично, пользовался обратными соображениями. Бруни использовал постулат изготовления смешенного кристалла, для произведения выводов о структуре одного из числа совместных кристаллизирующихся соединений, в то время как структура другого была известна, основано все на том, что для внедрения в решетку инородной молекулы нужно подобие формы молекул синоморфизм. Бруни имел мужество отстаивать правильность своих выводов даже в тех случаях, когда они находились в противоречии с химическими данными.


Разбираясь, в особенностях спектров органических соединяй в парафиновых матрицах при низких температурах. Во многих случаях связь внедряемой молекулы с решеткой растворителя невероятна, мала, что активатор можно рассматривать как ориентированный газ, в спектре кристаллическая матрица не производит изменений, так же проявляется небольшого смещения электронного перехода. В преобладающем числе событий, появляются сложности, состоящие из того, что в спектре появляются группы с близко расположенным линиями с разностями частот от 3-5 до нескольких десятков обратных сантиметров. Данные группы проявляются по всему спектру, расстояние остаётся неизменно, а условное название «мультиплеты». В элементарных вариациях таких как, у коронена, в состав групп входят пары линий-дублетов, в других случаях число компонент может быть значительно большим.

В тех случаях, когда резкий спектр является плодом нескольких растворителей, изображение спектра зависит от растворителя. В связи с интерпретацией дублетного спектра коронена Боуэн [19] высказал гипотезу, согласно которой сдвиг компонент мультиплета друг относительно друга обусловлено тем, что молекулы активатора могут фиксироваться в матрице в двух взаимно-перпендикулярных положениях. Эта гипотеза, однако, не в силахобъяснить происхождение мультиплетов, состоящих из большого числа компонент (до 7—8 мм).

Проблема, связанная с дискретный вариации представляет огромный интерес, с одной стороны от спектроскопии, с другой стороны если можно так выразиться тонкой структуры твердого тела.

В момент присутствие полиморфизма стремительное охлаждение до низких температур, вероятно, приведет к отвороченному существованию разных полиморфных форм в замершем растворителе и, зависит в какую форму попадет молекула активатора, где будет сдвиг ее энергии электронного перехода.

Нормальные парафины (и возможно длинноцепочечные органические молекулы) на самом деле являются полиморфными, как класс, это было подтверждено в работах Робертсана[20]. Полиморфизм, подтвержден как термическими данными, как и рентгеноструктурными, так и микроскопическими исследованиями, проявляется своеобразным путем. Имеется некая нормальная форма, в которой молекулы расположены таким образом, что длинные оси расположены перпендикулярно к прямоугольной ячейке, а период

Смотрите также файлы