Решить системы дифференциальных уравнений. Отрезок интегрирования выбрать произвольно. Интерполировать полученные решения. Найти точные решения. Построить графики.a) 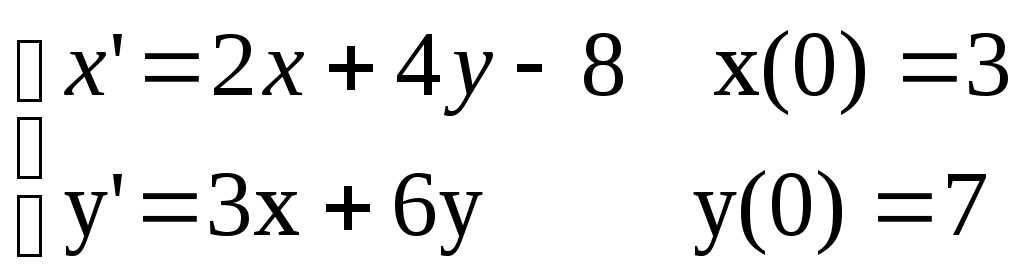b) 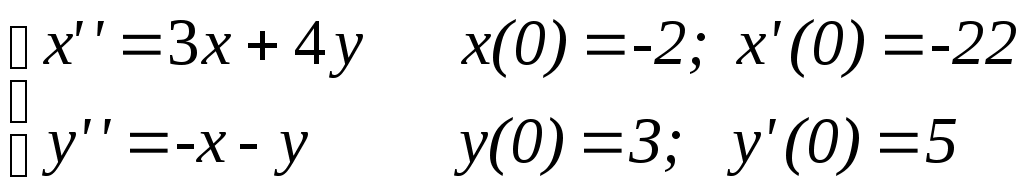Решение в Excel1 Задание № 1

Запишем систему уравнений в конечных разностях. Найдём значения x(t), y(t) в точках сетки. Запишем регрессионный многочлен третьей степени, найдём точное решение. Сравним полученные результаты графически.

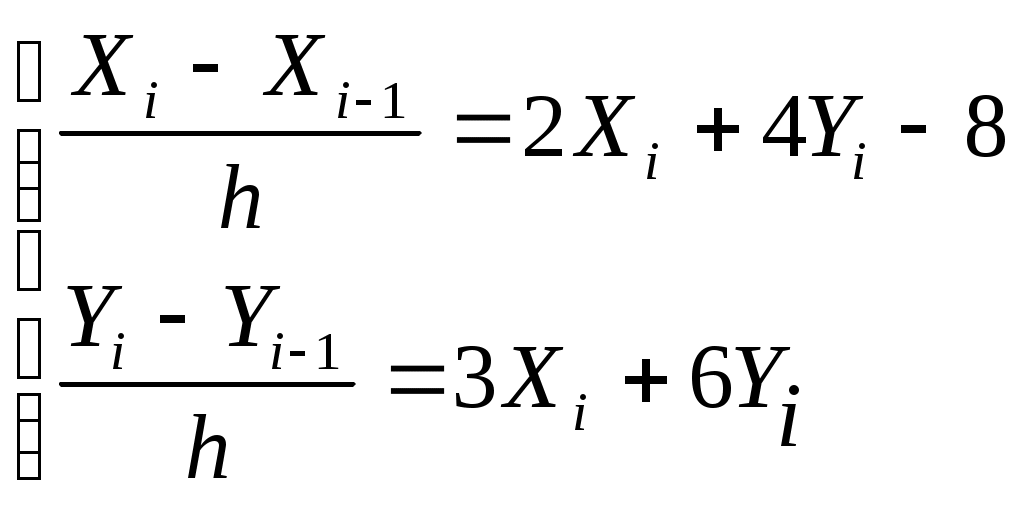
Разобьем отрезок [0; 1] на части с шагом h=0.1, получим узлы сетки X₀=0; x₁=0,2; x₂=0.4; …; t₁₀=1. Данную систему уравнений заменим конечно-разностными уравнениями. 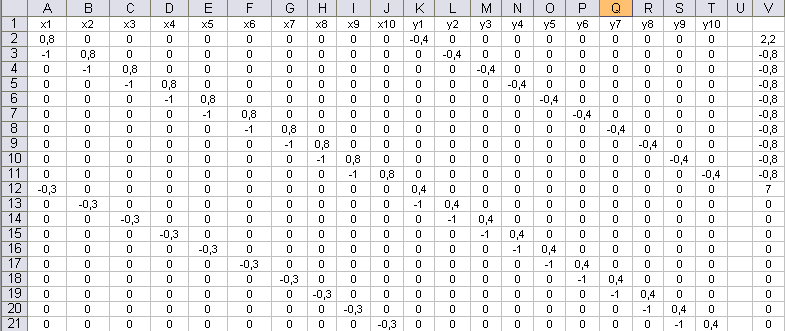Выполнив преобразования и записав уравнения для i=1…10, получим систему уравнений.Решим систему, найдем значения x₀ ,x₁… x₁₀, y₀ ,y₁… y₁₀ составим уравнение полиноминальной регрессии третьего порядка.Составленная система-таблица уравнений:Решение системы-таблицы

x	y
18,4	31,3
97,8	151,6
497,2	751,9
2496,6	3752,2
12496	18752
62495	93753
312495	468753
2E+06	2E+06
8E+06	1E+07
4E+07	6E+07
18,4	31,3

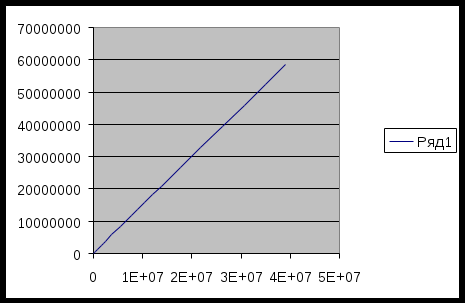
Построим графикРешение в MathCadЗадание №1Обозначим y₀

---

=x(t), y₁=y(t), y₂=x^/(t), y₃=y^/(t). Тогда система

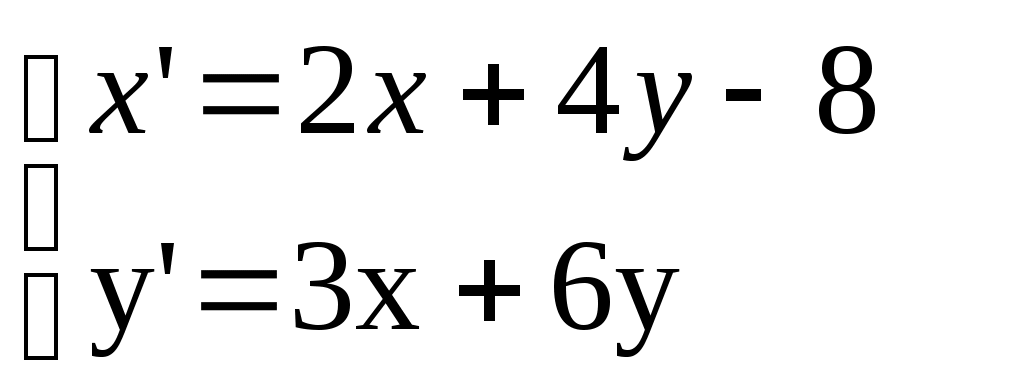
примет вид
,

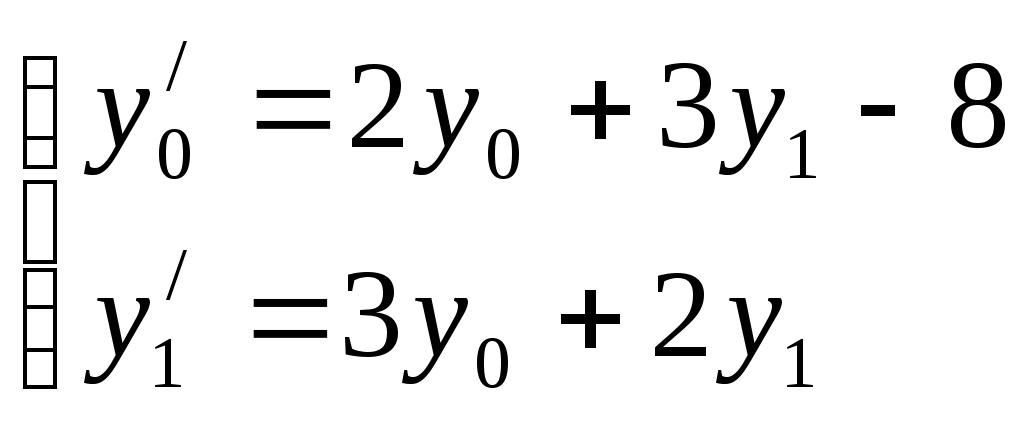вектор начальных условий

.
Решим полученную задачу методом Рунге-Кутта:

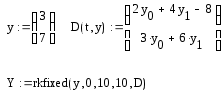
Построим графики x(t), y(t):



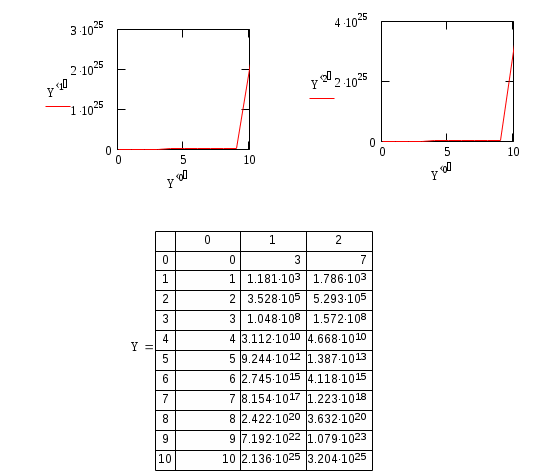
Составим регрессионные многочлены третьей степени для функций x(t), y(t):

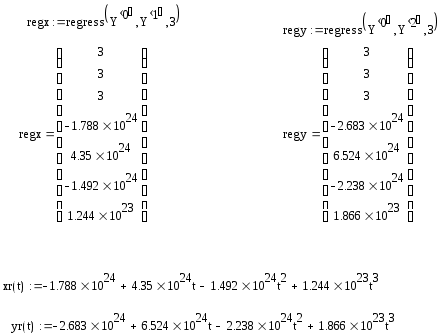
Построим графики приближенных значений и регрессионных значений этих функций. Очевидно, что погрешность регрессии невелика.



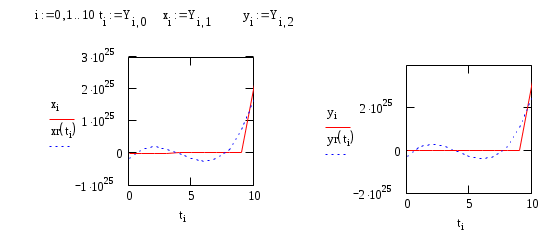
Задание №2
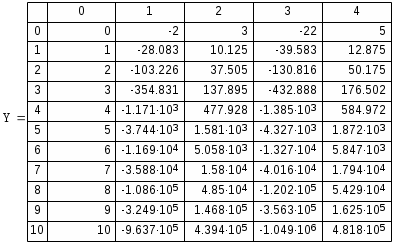
Обозначим y₀=x(t), y₁=y(t), y₂=x^/(t), y₃=y^/(t). Тогда система

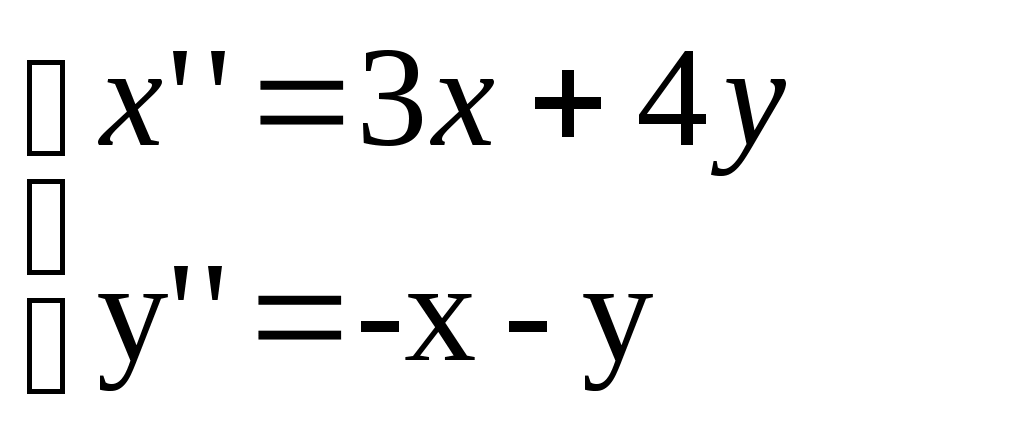
примет вид
,

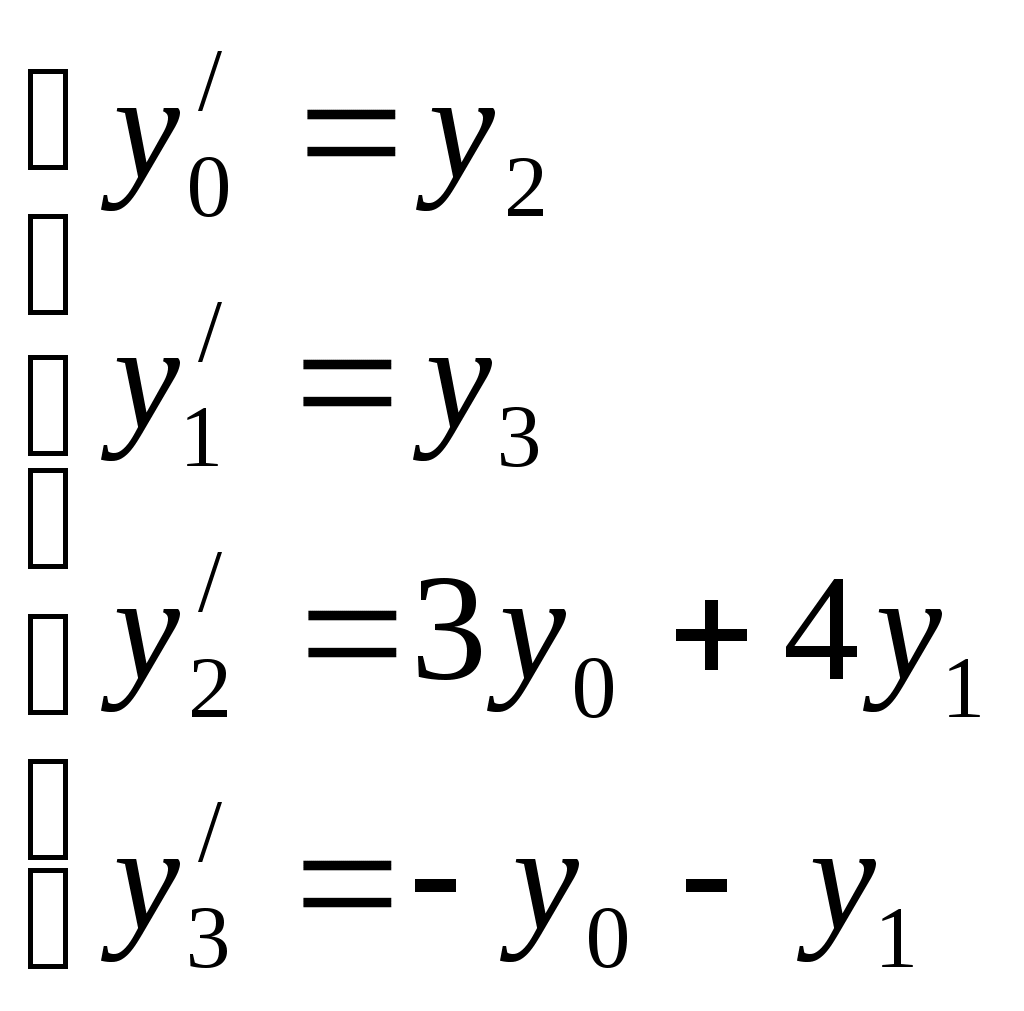вектор начальных условий .
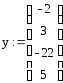Решим полученную задачу методом Рунге-Кутта:

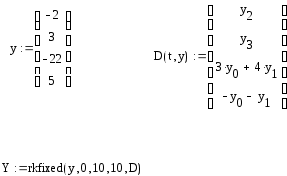
Построим графики x(t), y(t):




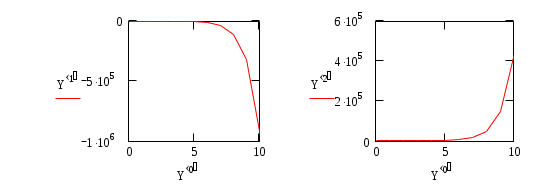
Составим регрессионные многочлены третьей степени для функций x(t), y(t):


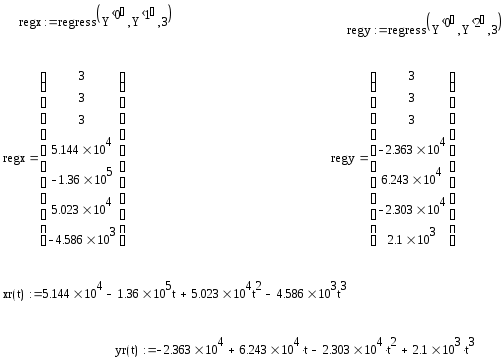
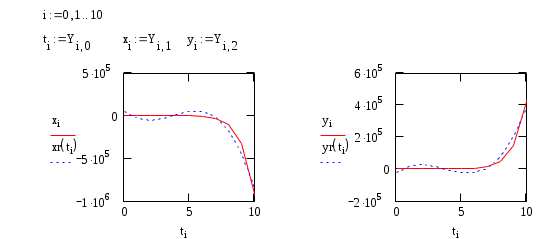
Построим графики приближенных значений и регрессионных значений этих функций. Очевидно, что погрешность регрессии невелика.




Министерство образования и науки РФ

Уфимский государственный нефтяной технический университет

Филиал УГНТУ в г. Салавате

Математика


РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Отчет по лабораторной работе № 7

ОПНН-170500-2.07.13 ЛР

---

Исполнитель:студент гр. МХ-03-21 М.М. ПаньшинРуководитель:ст. преподаватель       С. А. СаввинаСалават 2004Министерство образования и науки РФУфимский государственный нефтяной технический университетФилиал УГНТУ в г. СалаватеМатематикаРЕШЕНИЕ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙОтчет по лабораторной работе № 8ОПНН-170500-2.08.13 ЛРИсполнитель:студент гр. МХ-03-21 М.М. ПаньшинРуководитель:ст. преподаватель       С. А. СаввинаСалават 2004

---

Смотрите также файлы

• Программа по учебному предмету Русская литература призвана открыть перед учащимися новые возможности самовыражения. Она отвечает задачам современного школьного интегрированного образования учить учиться, учить думать, учить действовать, учить жить.docx

• Практическая работа 2 Чеклист анализа фрагмента учебного занятия химия 9 класс Предмет, класс.docx

• Институт нефтепереработки и нефтехимии фгбоу во угнту в г. Салавате.docx

• 1. Чистая прибыль.docx

• Методические рекомендации по организации и выполнению курсовой работы обучающимися колледжа qd 501. 10 Разработчик служба качества.pdf