ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 49
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования Российской Федерации
Тульский государственный университет
Кафедра "ТЕХНОЛОГИЯ МАШИНОСТРОЕНИЯ"
ИНФОРМАТИКА
Лабораторная работа №1
Системы счисления.
Методические указания
для подготовки бакалавров по направлению 552900 - "Технология, оборудование и автоматизация машиностроительных производств" дневного обучения
Тула 2001.
1. Перевод чисел из одной системы счисления в другую
Системой счисления называется совокупность символов, используемых для изображения чисел, т.е. кодирования числовой информации.
Системы счисления делятся на позиционные и непозиционные.
В непозиционной системе счисления местоположение символа определяющего цифру (число) не оказывает влияние на размер числа.
Примером такой системы является Римская система счисления.
Символы используемые в Римской системе счисления отображения чисел:
I - 1 , V - 5 , X - 10 , L - 50 , C - 100
Правило записи чисел: значение числа определяется суммой всех значений символов, расположенных правее максимального числа за вычетом значений символов, расположенных левее данного символа.
Примеры:
III (3), IV (4), XXII (22), XLI (41), LXXXIII (83)
Количество цифр применяемых в позиционной системе счисления называется основанием системы счисления p . Местоположение символа в числе называется разрядом, каждый разряд имеет свой вес.
В любой системе счисления число можно представить
Аn An-1 … A2 A1 A0, A--1 A-2 … A—m= An *pn + An-1 *pn-1 +…+ A2 *p2 + A1 *p1 + A0 *p0 + A-1 *p-1 + A-2 *p-2 +…+ A-m *p-m
Например:
345,16(10) = 3 * 102 + 4 * 101 + 5 * 100 + 1 * 10-1 * 6 * 10-2,
где (10) - основание десятичной системы счисления.
В вычислительной технике при кодировании информации широко используются двоичная, восьмеричная и шестнадцатиричная системы счисления, которые представлены в таблице 1.
Таблица 1
| Система счисления | |||
| двоичная | восмиричная | десятичная | шестнадцатиричная |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
| 10000 | 20 | 16 | 10 |
Чтобы перевести число из одной системы счисления в другую необходимо разделить его на основание той системы в которую оно переводится, полученный остаток будет младшим разрядом числа в новой системе счисления, частное от деления делится на основание, остаток - следующий разряд и так далее, деление продолжается до тех пор пока не получится частное меньше основания системы в которую мы переводим - это будет старший разряд число в новой системе счисления.
Например, перевести число 351 из десятичной системы счисления в шестнадцатиричную и двоичную:
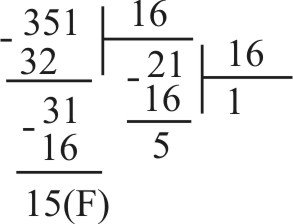
351(10) = 15F(16)
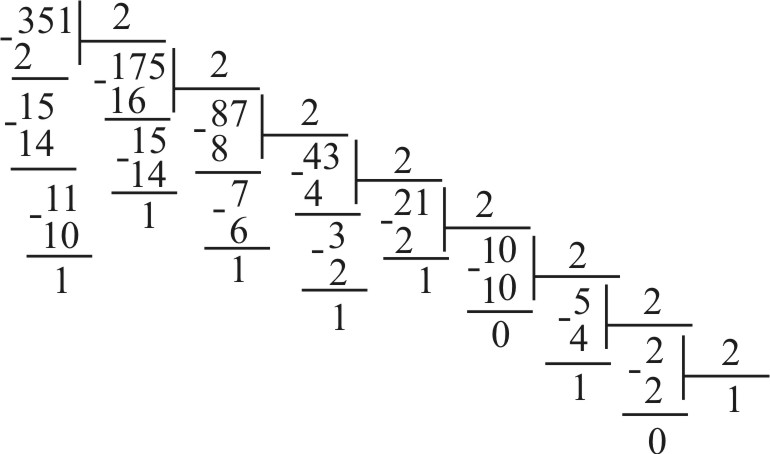
351(10) = 101011111(2)
Для перевода чисел из двоичной системы счисления в восьмеричную, шестнадцатиричную и наоборот можно воспользоваться следующим правилом: группа цифр из 3-х, 4-х двоичной системы заменяется на соответствующую цифру для восьмеричной, шестнадцатиричной системы и наоборот в соответствии с таблицей 2.
Например:
110 111 100 001(2) = 6741(8)
2305(8) = 010 011 000 101(2)
1111 0000 1011(2) = F0B(16)
577(16) = 0101 0111 0111(2)
Таблица 2
| Система счисления | |||
| двоичная | восьмиричная | двоичная | шестнадцатиричная |
| 000 | 0 | 0000 | 0 |
| 001 | 1 | 0001 | 1 |
| 010 | 2 | 0010 | 2 |
| 011 | 3 | 0011 | 3 |
| 100 | 4 | 0100 | 4 |
| 101 | 5 | 0101 | 5 |
| 110 | 6 | 0110 | 6 |
| 111 | 7 | 0111 | 7 |
| - | - | 1000 | 8 |
| - | - | 1001 | 9 |
| - | - | 1010 | А |
| - | - | 1011 | В |
| - | - | 1100 | С |
| - | - | 1101 | D |
| - | - | 1110 | E |
| - | - | 1111 | F |
2. Описание практической части работы:
2.1. Цели лабораторной работы: Ознакомиться с взаимным переводом чисел в двоичную, восьмиричную, десятичную и шестнадцатиричную системы счисления.
2.2. Постановка задачи: В соответствии с заданием осуществить взаимный перевод числа из двоичной, восьмиричной, десятичной и шестнадцатиричной систем счисления.
2.3. Порядок выполнения работы:
2.3.1. Ознакомиться с теоретической частью.
2.3.2. Получить задание у преподавателя.
2.3.3. Выполнить работу.
2.3.4. Оформить отчет:
2.3.4.1. Содержание отчета:
1. Цель работы - краткая формулировка поставленной цели.
2. Порядок выполнения - определяются действия, необходимые для выполнения данной работы.
3. Постановка задачи - формулирование задачи в соответствии с индивидуальным заданием.
4. Решение поставленной задачи:
4.1. Математическое описание решения поставленной задачи содержит описание связей между параметрами с использованием принятых в математике обозначений.
4.2. Описание логической структуры программы (алгоритм решения) содержит:
- краткое описание схемы программы,
- алгоритм решения (по ГОСТ ) - рисунок,
- краткое описание используемых операторов языка программирования (при необходимости).
4.3. Описание программы содержит:
- название файла, его размер,
- текст программы (или фрагмент для решения конкретной, наиболее важной части задания).
4.4. Результат работы программы:
- значения, полученные в результате выполнения программы
- анализ полученных результатов.
Выводы - отвечают на поставленную цель.
2.4. Контрольные вопросы:
1. Дайте определение системы счисления ?
2. Какие бывают системы счисления ?
3. Как записываются числа в позиционной системе счисления ?
4. Что называется основанием системы счисления ?
5. Как переводится заданное число из одной системы счисления в другую ?
6. Какое число больше 100(4) или 4(100) ?
7. Какое число больше 20(7) или 30(5) ?
8. Перевести в десятичную систему число 38(5) ?
9. Перевести число 222(8) в шестнадцатиричную систему счисления ?
10. Какое число больше 100(8) или XCLII
?
Таблица
задания:
| | Система счисления | |||
| nn | Двоичная | Восьмиричная | Десятичная | 16-иричная |
| 1 | 1111000111001010 | 131532 | 17523 | 6953 |
| 2 | 1110100000101011 | 165624 | 14915 | A4C2 |
| 3 | 1011011111011110 | 153645 | 32133 | 4334 |
| 4 | 1000000011011000 | 114424 | 10251 | A136 |
| 5 | 1001011110101110 | 177141 | 58516 | 9CA9 |
| 6 | 1000011001101111 | 133474 | 44736 | 5BA8 |
| 7 | 1101000000000100 | 153522 | 48255 | 6F89 |
| 8 | 1000101100111110 | 166367 | 25414 | 6663 |
| 9 | 1001110010000101 | 167265 | 14521 | 371A |
| 10 | 1011010100000110 | 121020 | 19816 | A625 |
| 11 | 1010110000001010 | 105150 | 45554 | 0499 |
| 12 | 1011000100111000 | 117621 | 27846 | 9D56 |
| 13 | 1000000010001110 | 152340 | 33457 | 2824 |
| 14 | 1011001010101111 | 157612 | 18633 | 1935 |
| 15 | 1101000000110011 | 164442 | 61627 | 2A71 |
| 16 | 1110011000001001 | 113341 | 48017 | CADA |
| 17 | 1000111110101010 | 155565 | 19827 | CCD9 |
| 18 | 1110110101001000 | 147545 | 29673 | 4EEA |
| 19 | 1011011000101101 | 133364 | 29544 | AB65 |
| 20 | 1000001100001010 | 102162 | 40274 | 1541 |
| 21 | 1000001101010100 | 112643 | 30299 | AAA1 |
| 22 | 1011101010110101 | 111136 | 32455 | 19D2 |
| 23 | 1011110111100100 | 126342 | 43673 | CF1F |
| 24 | 1101001111111111 | 136722 | 35186 | D098 |
| 25 | 1111000000011110 | 110504 | 15165 | D5B3 |
| 26 | 1010001101110110 | 123311 | 33907 | AE66 |
| 27 | 1010110110100001 | 156125 | 37856 | 786B |
| 28 | 1001000000110001 | 131642 | 20644 | B4FA |
| 29 | 1001000110101110 | 115264 | 61033 | BEBD |
| 30 | 1011101111001000 | 130275 | 60055 | 112D |