Файл: Примеры на составление программ для машины Тьюринга.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 105
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
необходимо освободить ячейку для нового символа  . Для этого на одну позицию влево нужно перенести первый символ (но на старом месте его можно пока не удалять), а далее, вернувшись на прежнее место, записать символ
. Для этого на одну позицию влево нужно перенести первый символ (но на старом месте его можно пока не удалять), а далее, вернувшись на прежнее место, записать символ  :
:

Рисунок 11.
Перенос символа на одну позицию влево схож с переносом символа вправо. Так же необходимо отметить, чтов состояниях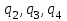 автомат может видеть только пустую клетку, а в состоянии
автомат может видеть только пустую клетку, а в состоянии 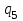 он видит первый символ входного слова, но никак не пустую клетку.
он видит первый символ входного слова, но никак не пустую клетку.
В виде программы для машины Тьюринга данную задачу можно записать следующим образом:
Таблица 4. Программа для примера 4.
Пример 5:
Пусть алфавит состоит из следующего набора символов: . Необходимо удалить из слова
. Необходимо удалить из слова  все вхождения символа
все вхождения символа  , если такие имеются.
, если такие имеются.
Решение:
В машине Тьюринга довольно сложно реализуются удаления символов из слов и вставки символов в слова. Поэтому иногда проще не сжимать или раздвигать входное слово, а формировать выходное слово в другом, свободном месте ленты.
Конкретно необходимо выполнить следующий ряд действий:

Рисунок 12.
Для этого необходимо проанализировать первый символ входного слова. Если это символ , то стираем его и переходим к следующему символу. Если же первый символ ˗это символ
, то стираем его и переходим к следующему символу. Если же первый символ ˗это символ  или
или  , тогда нужно стереть его и «пройти» вправо до первой пустой клетки , куда и записать данный символ.
, тогда нужно стереть его и «пройти» вправо до первой пустой клетки , куда и записать данный символ.
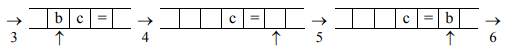
Рисунок 13.
Далее необходимо вернуться налево к тому символу, который стал первым во входном слове, и повторить те же самые действия, но уже по отношению к этому символу.
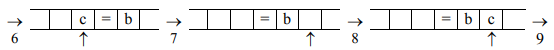
Рисунок 14.
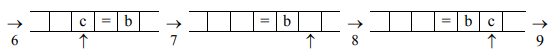
Рисунок 15.
С учётом всего сказанного и строится программу для машины Тьюринга. При этом необходимо отметить, что помимо символов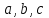 в процессе решения задачи на ленте появляется знак равенства, поэтому в таблице должен быть предусмотрен столбец и для этого знака.
в процессе решения задачи на ленте появляется знак равенства, поэтому в таблице должен быть предусмотрен столбец и для этого знака.
Таблица 5. Программа для примера 5.
Пример 1:
Заменить в двоичной записи числа все нули на единицы и все единицы на нули. Указатель стоит слева от числа.
Решение:
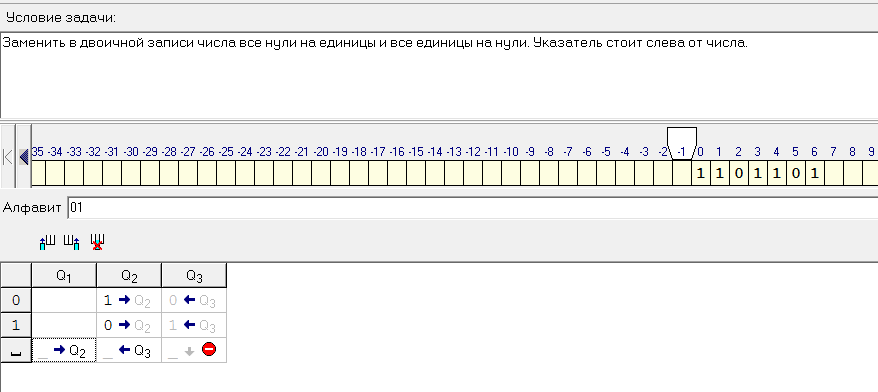
Рисунок 16.
Пример 2:
Дано три числа, разделенные пробелами. Необходимо пробелы, разделяющие данные числа заменить на запятые. Указатель стоит на первом левом непустом символе.
Решение:
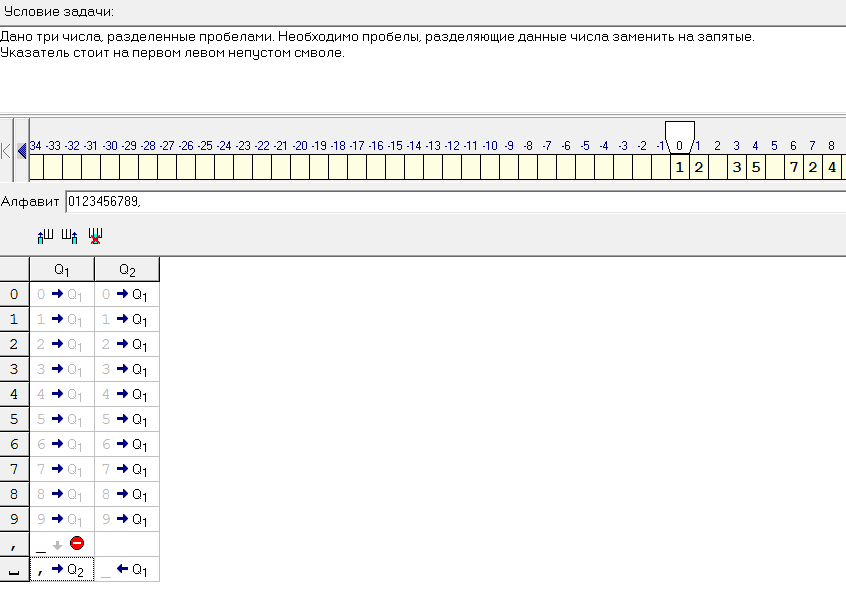
Рисунок 17.
Пример 3:
Дано число n в десятичной системе счисления. Разработайте машину Тьюринга, которая увеличивала бы заданное число на 7. Указатель находится на первом левом непустом символе.
Решение:
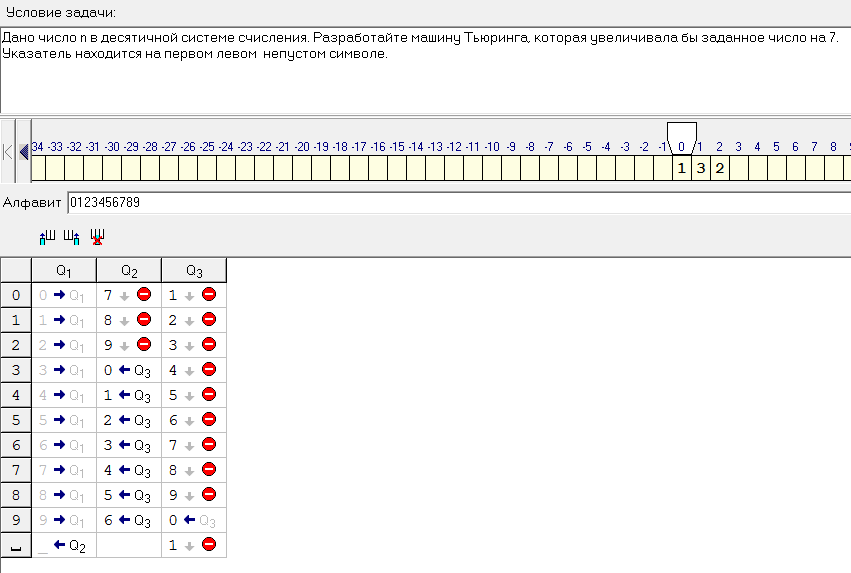
Рисунок 18.
Пример 4:
Пусть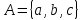 . Если первый и последний символы слова
. Если первый и последний символы слова  совпадают, то данное слово не менять, а иначе заменить то слово пустым символом.
совпадают, то данное слово не менять, а иначе заменить то слово пустым символом.
Решение:
Рисунок 19.
Пример 5:
Пусть . Необходимо удалить из слова
. Необходимо удалить из слова  его второй символ, если такой есть.
его второй символ, если такой есть.
Решение:
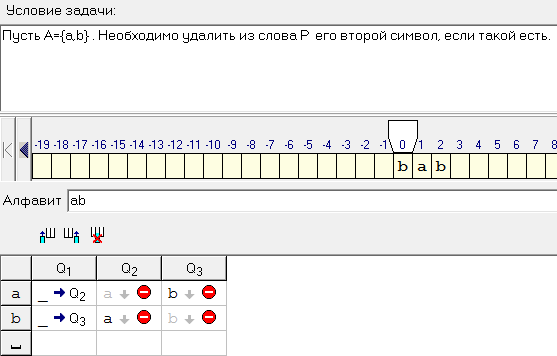
Рисунок 20.
Пример 6:
Пусть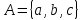 . Если
. Если  ˗ непустое слово, то необходимо за его первым символом вставить символ
˗ непустое слово, то необходимо за его первым символом вставить символ 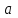 .
.
Решение:
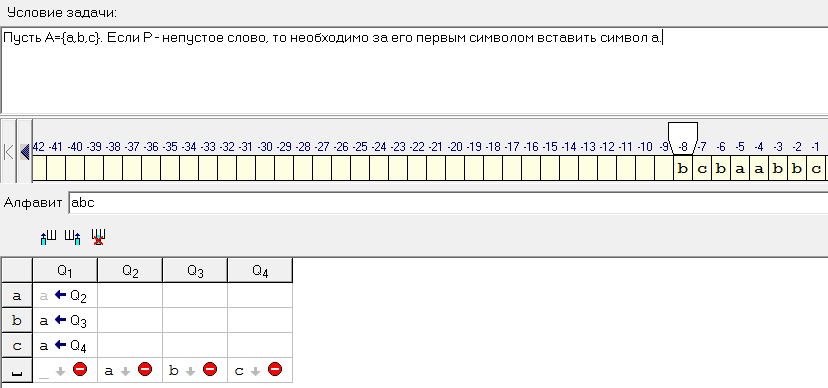
Рисунок 21.
Пример 7:
Пусть . Необходимо вставить в слово
. Необходимо вставить в слово  символ
символ  за первым символом
за первым символом  , если такой есть.
, если такой есть.
Решение:
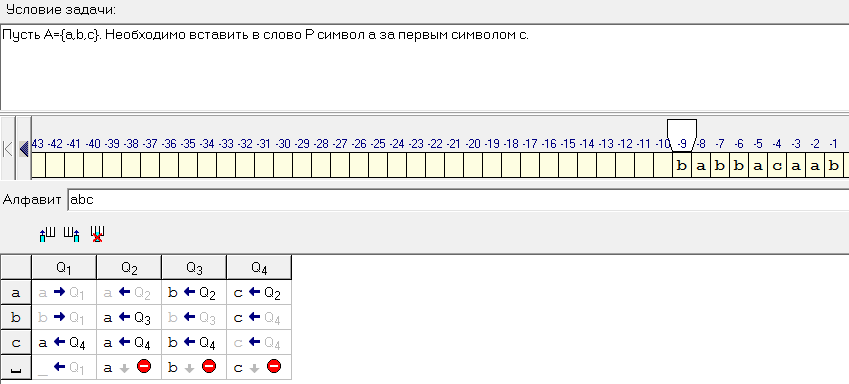
Рисунок 22.
Пример 8:
Пусть . Необходимо перенести первый символ непустого слова
. Необходимо перенести первый символ непустого слова  в его конец.
в его конец.
Решение:

Рисунок 23.
 . Для этого на одну позицию влево нужно перенести первый символ (но на старом месте его можно пока не удалять), а далее, вернувшись на прежнее место, записать символ
. Для этого на одну позицию влево нужно перенести первый символ (но на старом месте его можно пока не удалять), а далее, вернувшись на прежнее место, записать символ  :
:
Рисунок 11.
Перенос символа на одну позицию влево схож с переносом символа вправо. Так же необходимо отметить, чтов состояниях
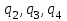 автомат может видеть только пустую клетку, а в состоянии
автомат может видеть только пустую клетку, а в состоянии 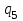 он видит первый символ входного слова, но никак не пустую клетку.
он видит первый символ входного слова, но никак не пустую клетку.В виде программы для машины Тьюринга данную задачу можно записать следующим образом:
Таблица 4. Программа для примера 4.
| |  |  | 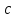 |  | комментарий |
 | 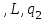 | 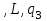 | 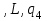 |  | Анализ первого символа для переноса его влево |
 | 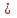 | 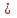 | 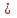 | 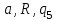 | Приписать  слева слева |
 | 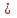 | 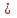 | 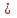 | 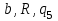 | Приписать  слева слева |
 | 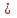 | 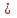 | 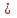 | 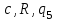 | Приписать 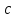 слева слева |
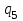 |  |  |  | 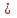 | Заменить бывший первый символ на  |
Пример 5:
Пусть алфавит состоит из следующего набора символов:
 . Необходимо удалить из слова
. Необходимо удалить из слова  все вхождения символа
все вхождения символа  , если такие имеются.
, если такие имеются.Решение:
В машине Тьюринга довольно сложно реализуются удаления символов из слов и вставки символов в слова. Поэтому иногда проще не сжимать или раздвигать входное слово, а формировать выходное слово в другом, свободном месте ленты.
Конкретно необходимо выполнить следующий ряд действий:
-
Выходное слово строится справа от входного. Чтобы разграничить эти слова, необходимо отделить их некоторым вспомогательным символом, например знаком =, который отличен от всех символов алфавита . На ленте могут быть записаны не только символы из алфавита входного слова.
. На ленте могут быть записаны не только символы из алфавита входного слова. -
После этого необходимо вернуться к началу входного слова:

Рисунок 12.
-
На данном этапе нужно перенести в цикле все символы входного слова, кроме символа , вправо за знак равенства в формируемое выходное слово.
, вправо за знак равенства в формируемое выходное слово.
Для этого необходимо проанализировать первый символ входного слова. Если это символ
 , то стираем его и переходим к следующему символу. Если же первый символ ˗это символ
, то стираем его и переходим к следующему символу. Если же первый символ ˗это символ  или
или  , тогда нужно стереть его и «пройти» вправо до первой пустой клетки , куда и записать данный символ.
, тогда нужно стереть его и «пройти» вправо до первой пустой клетки , куда и записать данный символ.Рисунок 13.
Далее необходимо вернуться налево к тому символу, который стал первым во входном слове, и повторить те же самые действия, но уже по отношению к этому символу.
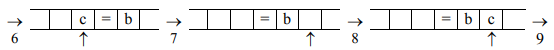
Рисунок 14.
-
Данный цикл завершается, когда при возврате налево в качестве первого символа появляется знак равенства. Это признак того, что полностью просмотрено входное слово и перенесены все его символы, которые отличны от , в формируемое справа выходное слово. Этот знак необходимо стереть, сдвинуться вправо под выходное слово и остановиться.
, в формируемое справа выходное слово. Этот знак необходимо стереть, сдвинуться вправо под выходное слово и остановиться.
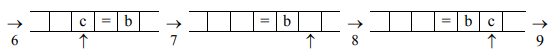
Рисунок 15.
С учётом всего сказанного и строится программу для машины Тьюринга. При этом необходимо отметить, что помимо символов
 в процессе решения задачи на ленте появляется знак равенства, поэтому в таблице должен быть предусмотрен столбец и для этого знака.
в процессе решения задачи на ленте появляется знак равенства, поэтому в таблице должен быть предусмотрен столбец и для этого знака.Таблица 5. Программа для примера 5.
| |  |  |  | = |  | комментарий |
 |  |  |  |  | 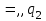 | Записать справа знак = |
 | 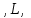 | 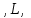 | 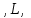 | 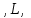 | 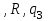 | Влево к первому символу слова |
 | 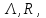 |  | 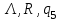 | 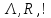 |  | Анализ и удаление его, разветвление |
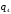 |  |  |  |  | 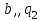 | Запись  справа, возврат налево справа, возврат налево |
 |  |  |  |  | 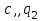 | Запись  справа, возврат налево справа, возврат налево |
§5. Примеры решения задач
Пример 1:
Заменить в двоичной записи числа все нули на единицы и все единицы на нули. Указатель стоит слева от числа.
Решение:

Рисунок 16.
Пример 2:
Дано три числа, разделенные пробелами. Необходимо пробелы, разделяющие данные числа заменить на запятые. Указатель стоит на первом левом непустом символе.
Решение:

Рисунок 17.
Пример 3:
Дано число n в десятичной системе счисления. Разработайте машину Тьюринга, которая увеличивала бы заданное число на 7. Указатель находится на первом левом непустом символе.
Решение:

Рисунок 18.
Пример 4:
Пусть
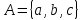 . Если первый и последний символы слова
. Если первый и последний символы слова  совпадают, то данное слово не менять, а иначе заменить то слово пустым символом.
совпадают, то данное слово не менять, а иначе заменить то слово пустым символом.Решение:

Рисунок 19.
Пример 5:
Пусть
 . Необходимо удалить из слова
. Необходимо удалить из слова  его второй символ, если такой есть.
его второй символ, если такой есть.Решение:

Рисунок 20.
Пример 6:
Пусть
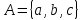 . Если
. Если  ˗ непустое слово, то необходимо за его первым символом вставить символ
˗ непустое слово, то необходимо за его первым символом вставить символ 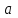 .
.Решение:

Рисунок 21.
Пример 7:
Пусть
 . Необходимо вставить в слово
. Необходимо вставить в слово  символ
символ  за первым символом
за первым символом  , если такой есть.
, если такой есть.Решение:

Рисунок 22.
Пример 8:
Пусть
 . Необходимо перенести первый символ непустого слова
. Необходимо перенести первый символ непустого слова  в его конец.
в его конец.Решение:

Рисунок 23.