Файл: Примеры на составление программ для машины Тьюринга.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 106
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Примеры на составление программ для машины Тьюринга
Для сокращения формулировки задач введем следующие обозначения:
-
Буквой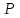 будем обозначать входное слово;
будем обозначать входное слово; -
Буквой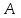 будем обозначать алфавит входного слова, то есть набор тех символов, из которых может состоять
будем обозначать алфавит входного слова, то есть набор тех символов, из которых может состоять 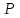 . Однако, необходимо отметить, что в выходных и промежуточных словах могут появляться и другие символы.
. Однако, необходимо отметить, что в выходных и промежуточных словах могут появляться и другие символы.
Пример 1:
Перемещение автомата. Замена символов.
Пусть
 , а
, а 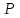 ˗ это непустое слово. Значит
˗ это непустое слово. Значит 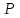 ˗ это последовательность из десятичных цифр, то есть запись целого неотрицательного числа в десятичной системе. Необходимо получить на ленте запись числа, которое на 1 больше числа
˗ это последовательность из десятичных цифр, то есть запись целого неотрицательного числа в десятичной системе. Необходимо получить на ленте запись числа, которое на 1 больше числа 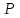 .
.Решение:
Для решения данной задачи необходимо выполнить ряд действий:
-
Перегнать автомат под последнюю цифру числа; -
Если это цифра от 0 до 8, то заменить ее цифрой на 1 больше и остановиться;
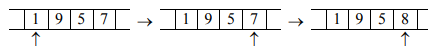
Рисунок 3.
-
Если же это цифра 9, то заменить ее на 0 и сдвинуть автомат к предыдущей цифре, после чего таким же способом увеличить на 1 эту предпоследнюю цифру;
Рисунок 4.
-
Особый случай составляет тот, когда в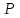 имеются только девятки (например, 99). В данном случае автомат будет сдвигаться влево, заменяя девятки на нули, и в конце концов окажется под пустой клеткой. Тогда именно в эту пустую клетку необходимо записать 1 и остановиться (ответом будет 100):
имеются только девятки (например, 99). В данном случае автомат будет сдвигаться влево, заменяя девятки на нули, и в конце концов окажется под пустой клеткой. Тогда именно в эту пустую клетку необходимо записать 1 и остановиться (ответом будет 100):

Рисунок 5.
В виде программы для МТ эти действия описываются следующим образом:

Рисунок 6.
Пояснения:
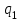 ˗ это состояние, в котором автомат переходит под последнюю цифру числа. Для этого он постоянно движется вправо, не меняя видимые цифры и оставаясь в том же состоянии. Однако, определить последнюю цифру автомат может, только попав на соседнюю пустую клетку. Поэтому, дойдя до пустой клетки, он возвращается под последнюю цифру и переходит в состояние
˗ это состояние, в котором автомат переходит под последнюю цифру числа. Для этого он постоянно движется вправо, не меняя видимые цифры и оставаясь в том же состоянии. Однако, определить последнюю цифру автомат может, только попав на соседнюю пустую клетку. Поэтому, дойдя до пустой клетки, он возвращается под последнюю цифру и переходит в состояние 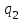 .
. 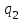 ˗ это состояние, в котором автомат прибавляет 1 к той цифре, которую в данный момент видит. Сначала это последняя цифра, если она находится в диапазоне от 0 до 8, то он прибавляет к ней 1 и останавливается, если нет, то возвращается и проверяет предпоследнюю цифру и т.д.
˗ это состояние, в котором автомат прибавляет 1 к той цифре, которую в данный момент видит. Сначала это последняя цифра, если она находится в диапазоне от 0 до 8, то он прибавляет к ней 1 и останавливается, если нет, то возвращается и проверяет предпоследнюю цифру и т.д.Пример 2:
Пусть
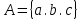 . Необходимо перенести первый символ непустого слова
. Необходимо перенести первый символ непустого слова  в его конец.
в его конец. Например,
Рисунок 7.
Решение:
Для решения данной задачи необходимо выполнить ряд следующих действий:
1. На первом шаге необходимо запомнить первый символ слова
 , а затем стереть данный символ.
, а затем стереть данный символ. 2. На втором шаге необходимо перегнать автомат вправо под первую пустую клетку за
 и записать в неё символ, который был запомнен на первом шаге.
и записать в неё символ, который был запомнен на первом шаге. Для того, чтобы запомнить первый символ необходимо использовать различные состояния автомата. Если первым символом оказался символ
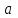 , то необходимо перейти в состояние
, то необходимо перейти в состояние 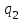 , в котором автомат бежит вправо и записывает в конце
, в котором автомат бежит вправо и записывает в конце 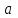 . Если же первым символом оказался символ
. Если же первым символом оказался символ
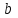 , тогда необходимо перейти в состояние
, тогда необходимо перейти в состояние  , где происходят все те же действия, только в конце записывается символ
, где происходят все те же действия, только в конце записывается символ 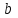 . Если же, в свою очередь, первый символ был
. Если же, в свою очередь, первый символ был  , тогда необходимо перейти в состояние
, тогда необходимо перейти в состояние  , в котором автомат дописывает в конце слова символ
, в котором автомат дописывает в конце слова символ  . Следовательно, фиксируется переводом автомата в разные состояния именно то, каким был первый символ. Это один из типичных приёмов при программировании на машине Тьюринга.
. Следовательно, фиксируется переводом автомата в разные состояния именно то, каким был первый символ. Это один из типичных приёмов при программировании на машине Тьюринга.С учетом всего вышеприведенного программа будет выглядеть следующим образом:
Таблица 2. Программа для задачи 2.
| |  | 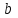 |  | 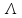 | комментарий |
 |  | 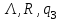 | 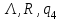 |  | Анализ 1-го символа, удаление его, разветвление |
 |  |  |  | 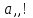 | Запись  справа справа |
 |  |  |  | 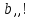 | Запись 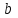 справа справа |
 |  |  |  | 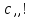 | Запись  справа справа |
Так же можно рассмотреть поведение данной программы на входных словах, которые содержат не более одного символа.
Если входное слово пусто (такое слово называется «плохим» для задачи), то в данном случае программа зациклится, то есть автомат, находясь в состоянии
 и все время попадая на пустые клетки, будет двигаться бесконечно вправо.
и все время попадая на пустые клетки, будет двигаться бесконечно вправо.Если же входное слово оказывается равным только одному символу, то в таком случае автомат сотрет данный символ, сдвинется на одну клетку вправо и запишет в нее этот символ:

Рисунок 8.
Таким образом, можно сказать, что в том случае, если слово состоит из одного символа, то оно просто сдвинется на одну клетку вправо. Это допустимо, так как клетки не нумерованы. Именно поэтому местоположение слова в ленте никак не фиксируется и перемещение слова вправо или влево относительно исходного положения заметить невозможно. В связи с данной особенностью совсем необязательно, чтобы выходное слово находилось там же, где и находилось входное. Результат может оказаться правее или левее этого места.
Пример 3:
Пусть
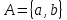 . Необходимо удалить из слова
. Необходимо удалить из слова  его второй символ, если такой есть.
его второй символ, если такой есть.Решение:
С первого взгляда на данную задачу, кажется, что решить ее довольно просто: для этого нужно сдвинуть автомат под клетку со вторым символом и затем, после проделанного, очистить данную клетку:

Рисунок 9.
Однако, необходимо сказать, что внутри входного слова не должны находиться пустые клетки. Именно поэтому, после удаления второго символа необходимо «сжать» слово, тем самым перенеся первый символ на одну клетку вправо. Для этого автомат должен вернуться к первому символу, запомнить его и стереть, а затем, опять сдвинувшись вправо записать его в ячейку, где находился второй символ. Однако заметим то, что начальный шаг вправо ко второму символу, чтобы его стереть, и последующий возврат к первому символу являются лишними действиями, так как нет разницы между переносом первого символа в пустую клетку и клетку с каким-то символом. Именно поэтому необходимо зразу запомнить первый символ, стереть его и записать вместо второго символа:

Рисунок 10.
В виде программы для машины Тьюринга это можно записать следующим образом:
Таблица 3. Программа для задачи 3.
| |  |  |  | комментарий |
 |  |  |  | Анализ и удаление первого символа |
 |  |  |  | Замена второго символа на  |
 |  |  |  | Замена второго символа на  . . |
Пример 4.
Пусть
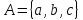 . Если
. Если  является непустым словом, то необходимо за его первым символом вставить символ
является непустым словом, то необходимо за его первым символом вставить символ  .
.Решение:
Понятно, что между вторым и первым символами слова
