ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 29
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Общие решение для периодических сигналов:
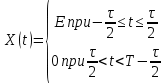
Тогда получим:
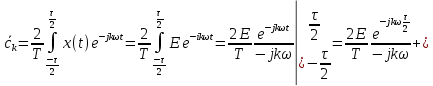
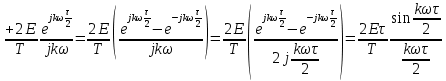
Выражение для амплитудного частотного спектра:
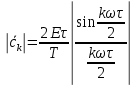
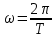, тогда выражение для амплитудного спектра примет вид: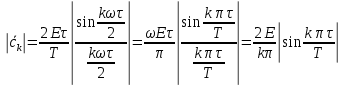
1. Построить временные диаграммы, рассчитать и построить в масштабе амплитудные спектры следующих сигналов:
Для выполнения пунктов 1-3 первого задания использовалась следующая
1. Построим временные диаграммы, рассчитаем и построить в масштабе амплитудные
спектры :
1. Листинг программы на языке Matlab:
>> t = 1:3:10; U0=15; T=3; phi=0;
>> s=U0*sin(2*pi*T*t+phi);
>> plot(t, square(t,20))
Временная диаграмма имеет вид:
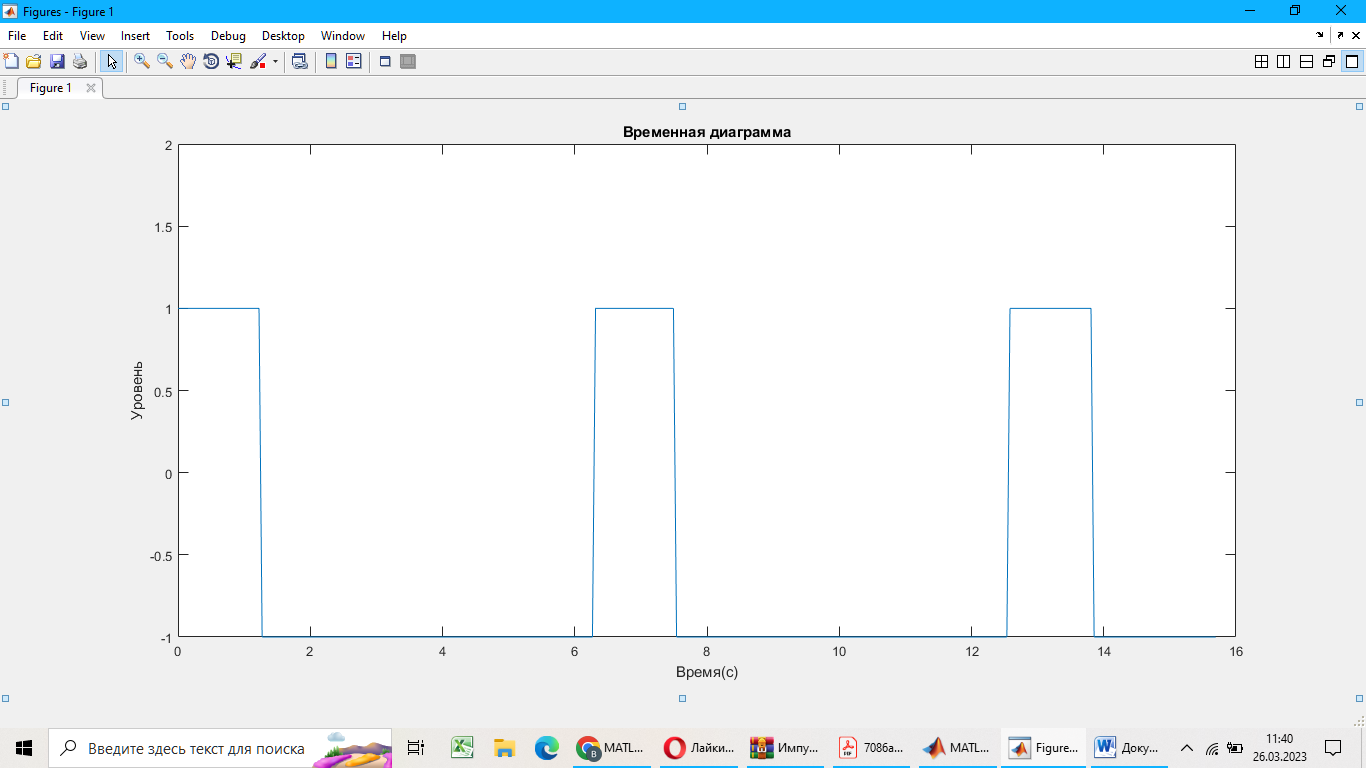
Рисунок 1
Рассчитаем и построим амплитудные спектры сигнала:
% Файл - сценарий для построения графиков спектров
T = 3; % период сигнала
w0 = 2*pi/T; % основная частота
hold on, grid on
y = (2./(pi.*x)).*abs(sin(pi.*x.*tay./T)); % амплитудный спектр
y_dot = (2./(pi.*x_dot)).*abs(sin(pi.*x_dot.*tay./T)); % значение амплитудного спектра в кратных точках
plot(x, y, '--')
plot(x_dot, y_dot, 'r*')
n1=1:10; % положительные номера гармоник
cn=-4*j./n1/pi.*sin(pi*n1/6).*sin(n1*pi/2).*exp(-j*n1*pi/3);
n2=-15:-1;1 % отрицательные номера гармоник
c_n=-4*j./n2/pi.*sin(pi*n2/6).*sin(n2*pi/2).*exp(-j*n2*pi/3);
Xn=[c_n 0 cn]; % вектор коэффициентов Фурье для n>0, n=0, n<0
n=-10:10; % вектор номеров гармоник
figure(1), subplot(121),stem(n*w0,abs(Xn))
Амплитудный спектр имеет вид:
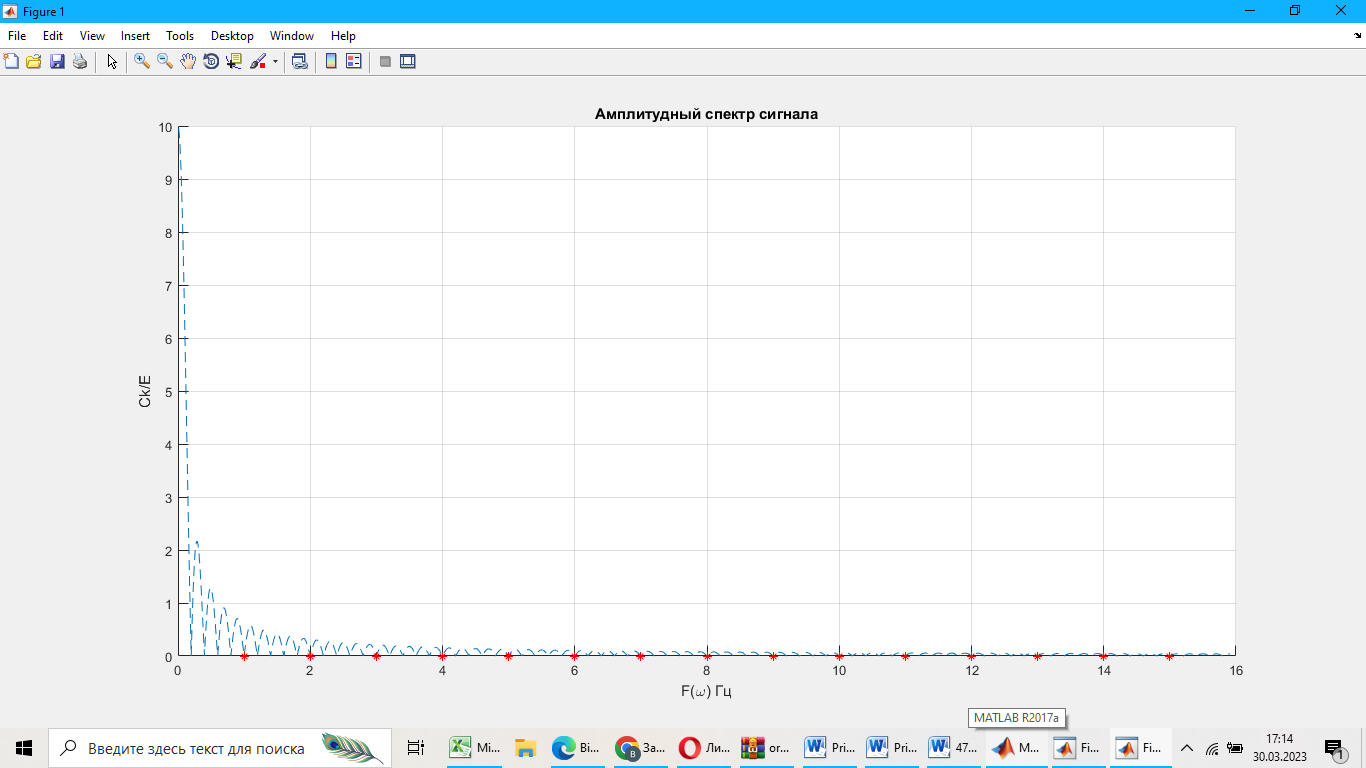
Рисунок 2
2. Листинг программы на языке Matlab:
>> t = 1:1.5:10; U0=15; T=3; phi=0;
>> s=U0*sin(2*pi*T*t+phi);
>> plot(t, square(t,20))
Временная диаграмма имеет вид:
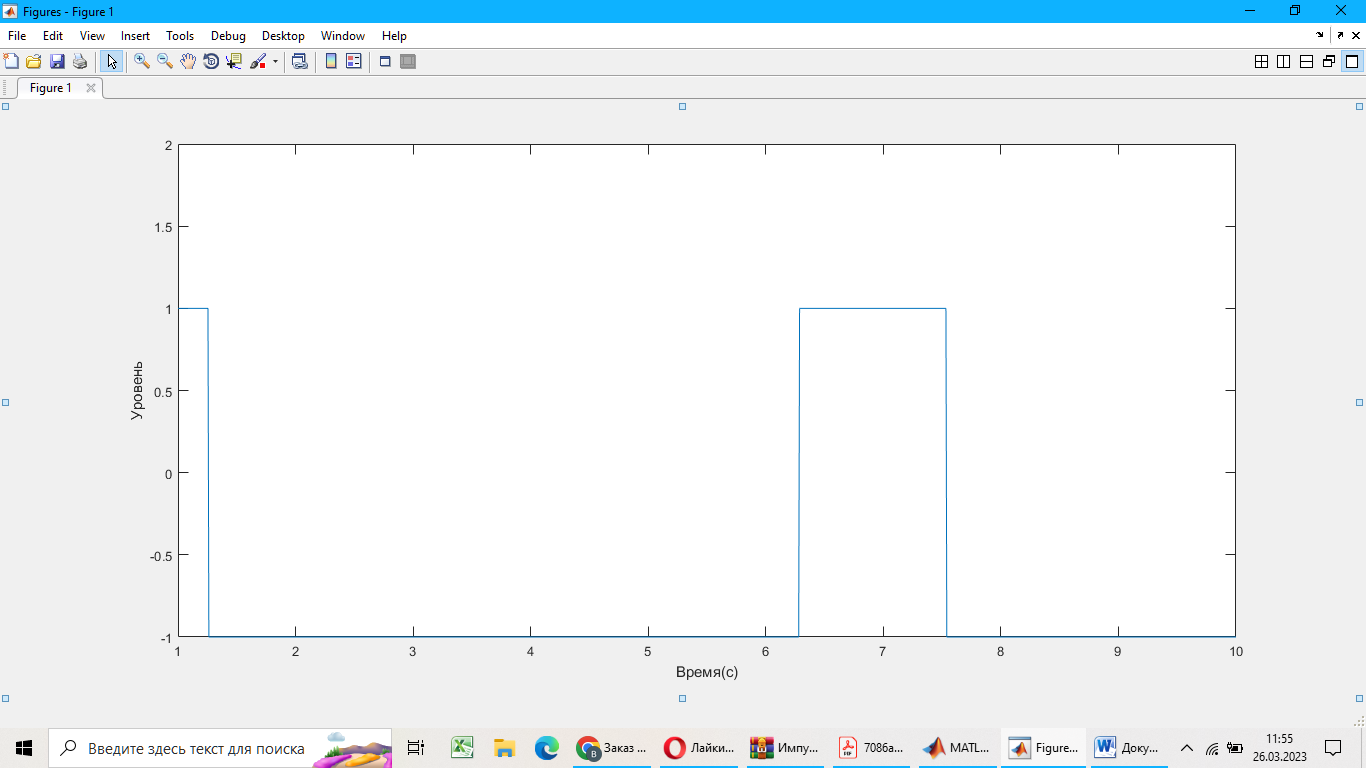
Рисунок 3
Рассчитаем и построим амплитудные спектры сигнала:
% Файл - сценарий для построения графиков спектров
T = 3; % период сигнала
w0 = 2*pi/T; % основная частота
hold on, grid on
y = (2./(pi.*x)).*abs(sin(pi.*x.*tay./T)); % амплитудный спектр
y_dot = (2./(pi.*x_dot)).*abs(sin(pi.*x_dot.*tay./T)); % значение амплитудного спектра в кратных точках
plot(x, y, '--')
plot(x_dot, y_dot, 'r*')
n1=1:10; % положительные номера гармоник
cn=-4*j./n1/pi.*sin(pi*n1/6).*sin(n1*pi/2).*exp(-j*n1*pi/3);
n2=-15:-1;1 % отрицательные номера гармоник
c_n=-4*j./n2/pi.*sin(pi*n2/6).*sin(n2*pi/2).*exp(-j*n2*pi/3);
Xn=[c_n 0 cn]; % вектор коэффициентов Фурье для n>0, n=0, n<0
n=-10:10; % вектор номеров гармоник
figure(1), subplot(121),stem(n*w0,abs(Xn))
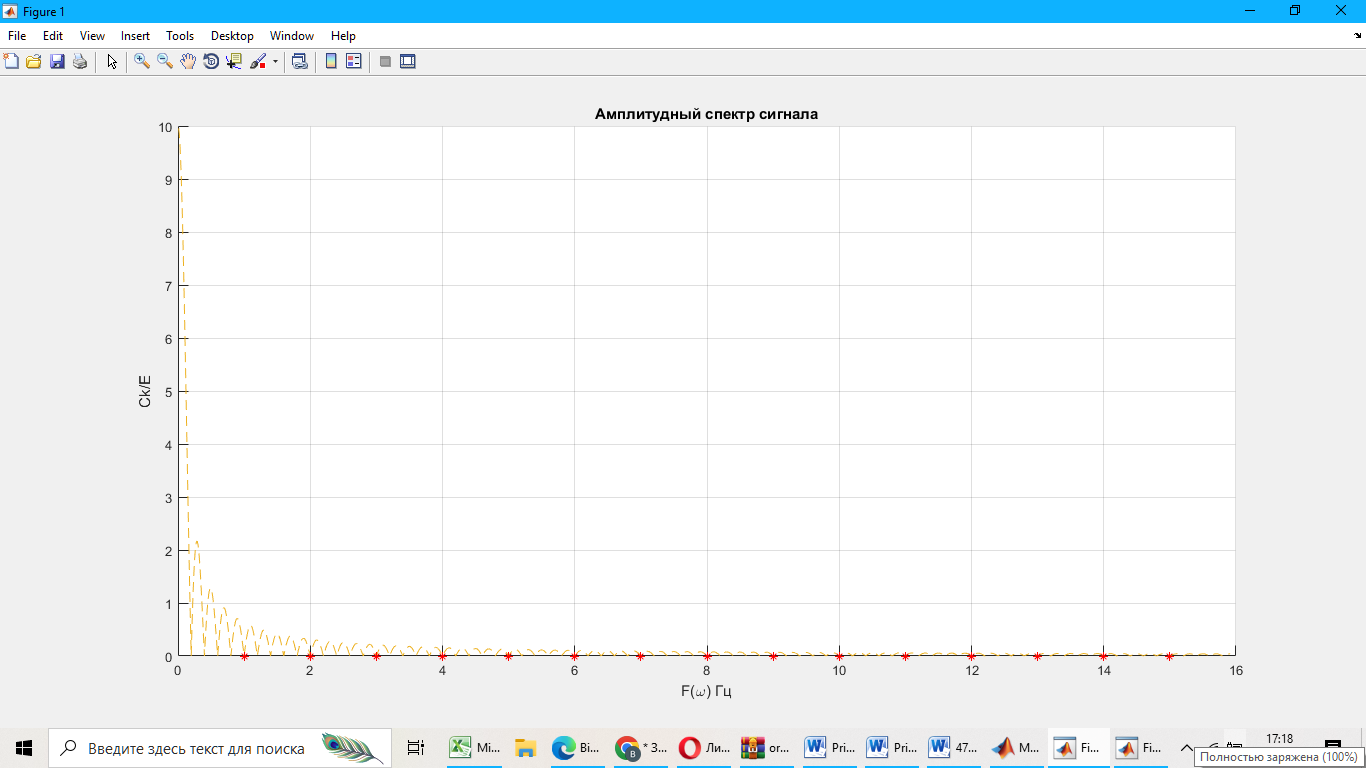
Рисунок 4
3. Листинг программы на языке Matlab:
>> t = 1:6:10; U0=15; T=6; phi=0;
>> s=U0*sin(2*pi*T*t+phi);
>> plot(t, square(t,20))
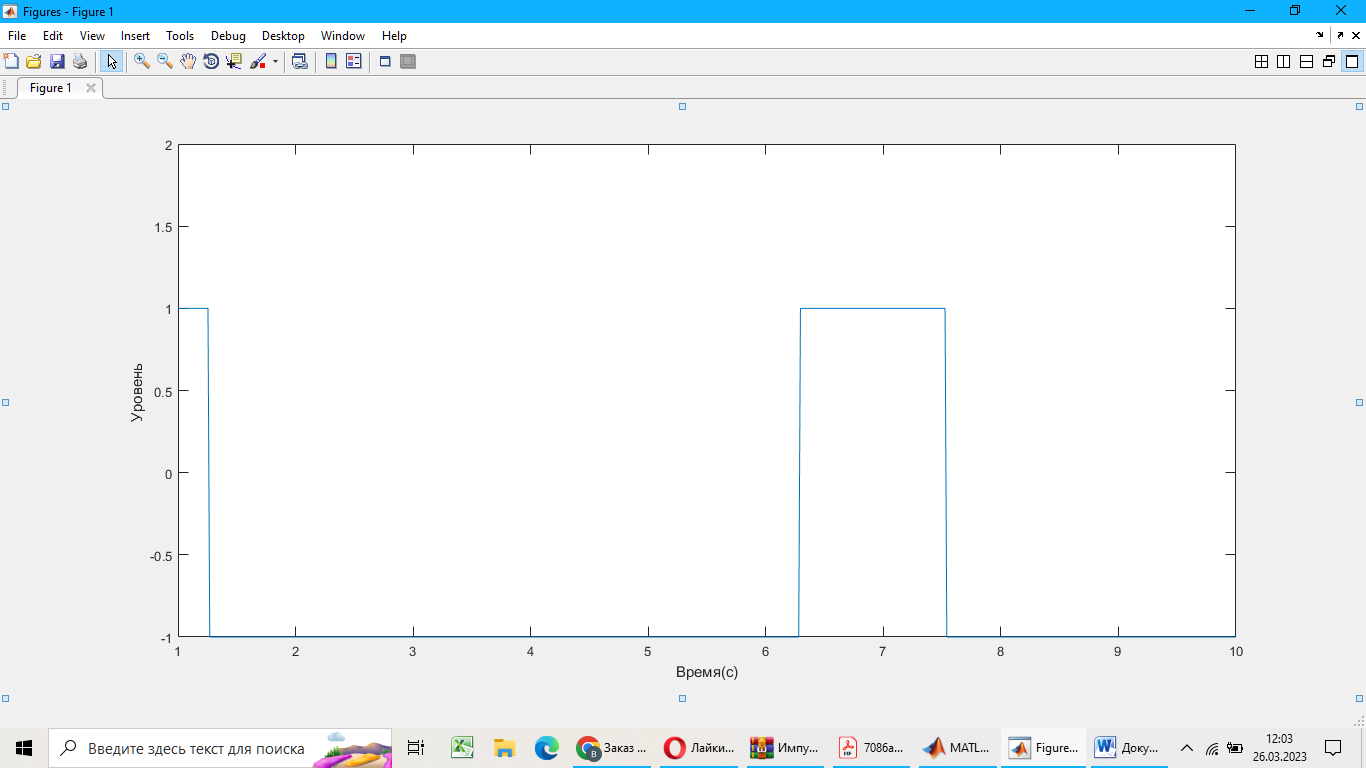
Рисунок 5
Рассчитаем и построим амплитудные спектры сигнала:
% Файл - сценарий для построения графиков спектров
T = 6; % период сигнала
w0 = 2*pi/T; % основная частота
hold on, grid on
y = (2./(pi.*x)).*abs(sin(pi.*x.*tay./T)); % амплитудный спектр
y_dot = (2./(pi.*x_dot)).*abs(sin(pi.*x_dot.*tay./T)); % значение амплитудного спектра в кратных точках
plot(x, y, '--')
plot(x_dot, y_dot, 'r*')
n1=1:10; % положительные номера гармоник
cn=-4*j./n1/pi.*sin(pi*n1/6).*sin(n1*pi/2).*exp(-j*n1*pi/3);
n2=-15:-1;1 % отрицательные номера гармоник
c_n=-4*j./n2/pi.*sin(pi*n2/6).*sin(n2*pi/2).*exp(-j*n2*pi/3);
Xn=[c_n 0 cn]; % вектор коэффициентов Фурье для n>0, n=0, n<0
n=-10:10; % вектор номеров гармоник
figure(1), subplot(121),stem(n*w0,abs(Xn))
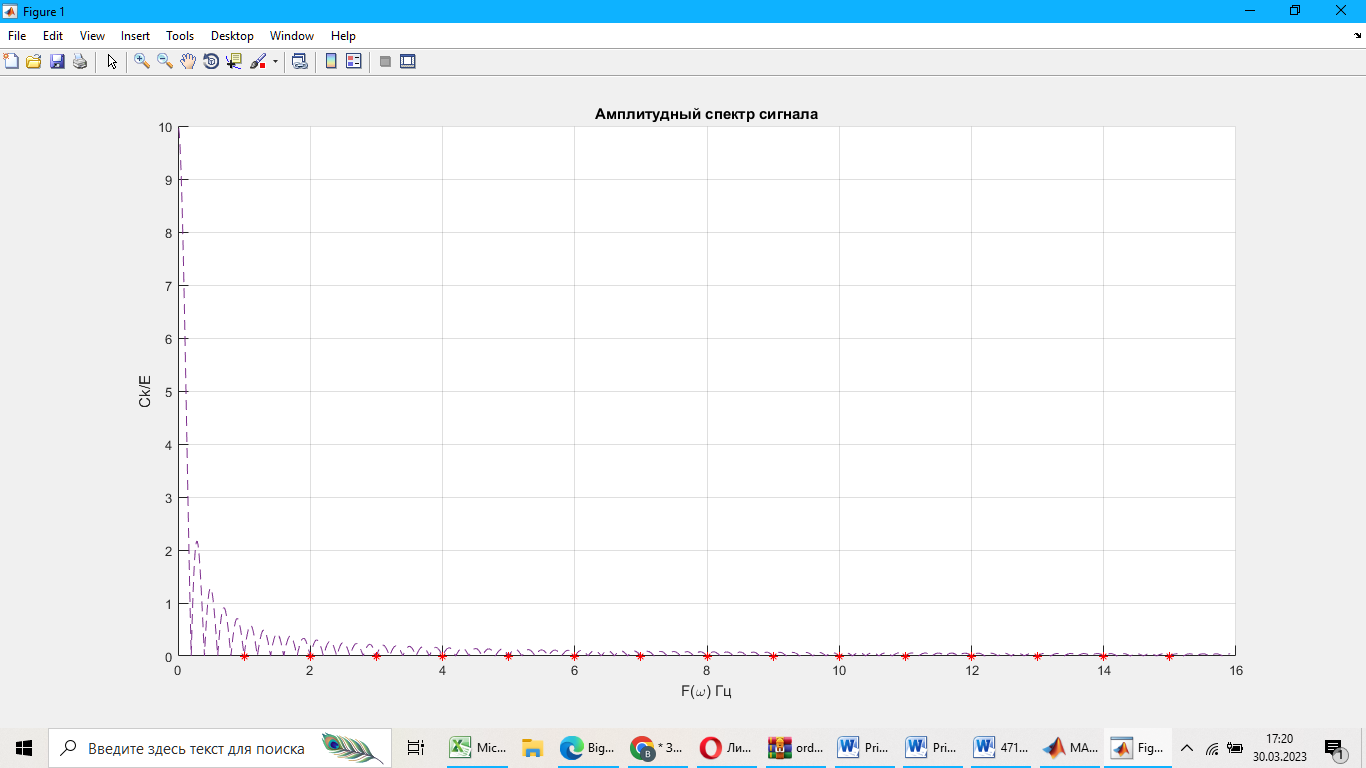
Рисунок 6
4. Листинг программы на языке Matlab:
>> t = 1:0.015:10; U0=15; T=1; phi=0;
>> s=U0*sin(2*pi*T*t+phi);
>> plot(t, square(t,20))
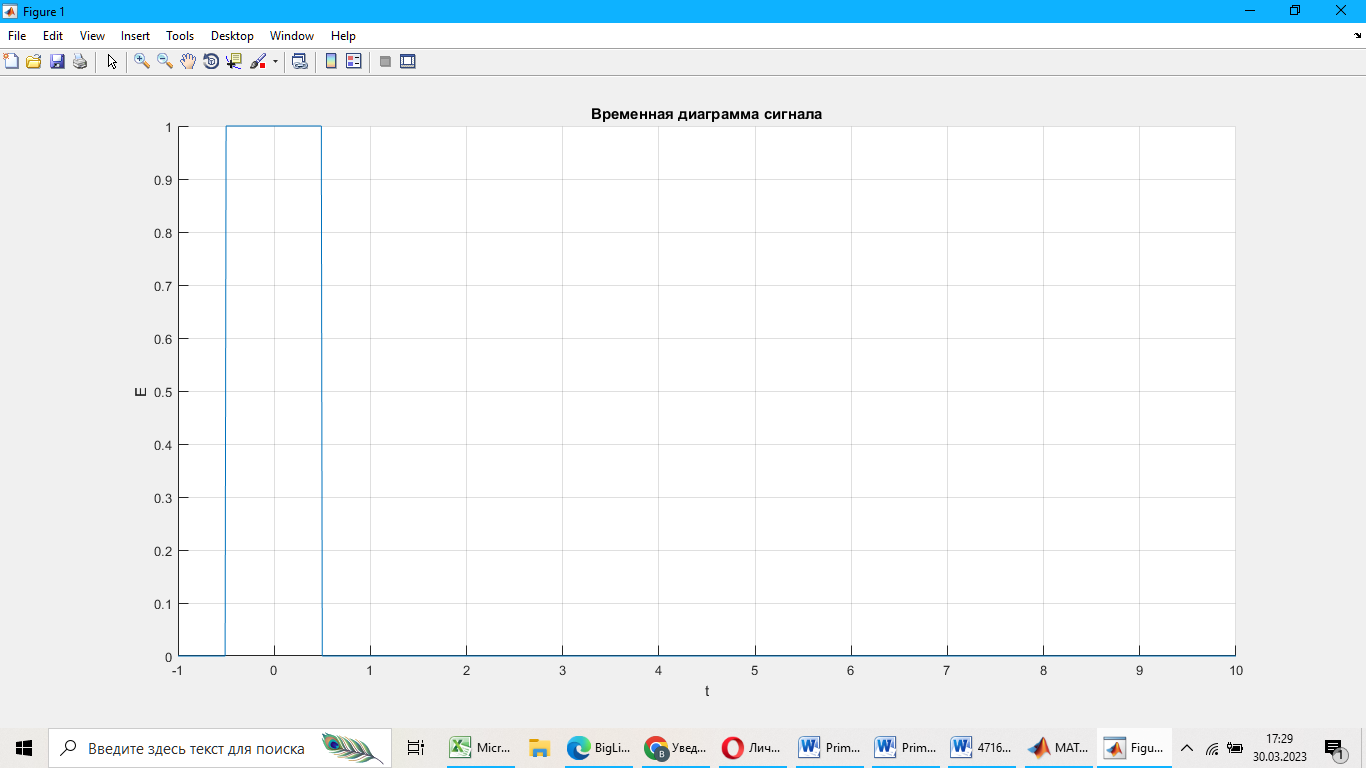
Рисунок 7
Рассчитаем и построим амплитудные спектры сигнала:
% Файл - сценарий для построения графиков спектров
T = 1; % период сигнала
w0 = 2*pi/T; % основная частота
hold on, grid on
y = (2./(pi.*x)).*abs(sin(pi.*x.*tay./T)); % амплитудный спектр
y_dot = (2./(pi.*x_dot)).*abs(sin(pi.*x_dot.*tay./T)); % значение амплитудного спектра в кратных точках
plot(x, y, '--')
plot(x_dot, y_dot, 'r*')
n1=1:10; % положительные номера гармоник
cn=-4*j./n1/pi.*sin(pi*n1/6).*sin(n1*pi/2).*exp(-j*n1*pi/3);
n2=-15:-1;1 % отрицательные номера гармоник
c_n=-4*j./n2/pi.*sin(pi*n2/6).*sin(n2*pi/2).*exp(-j*n2*pi/3);
Xn=[c_n 0 cn]; % вектор коэффициентов Фурье для n>0, n=0, n<0
n=-15:15; % вектор номеров гармоник
figure(1), subplot(121),stem(n*w0,abs(Xn))
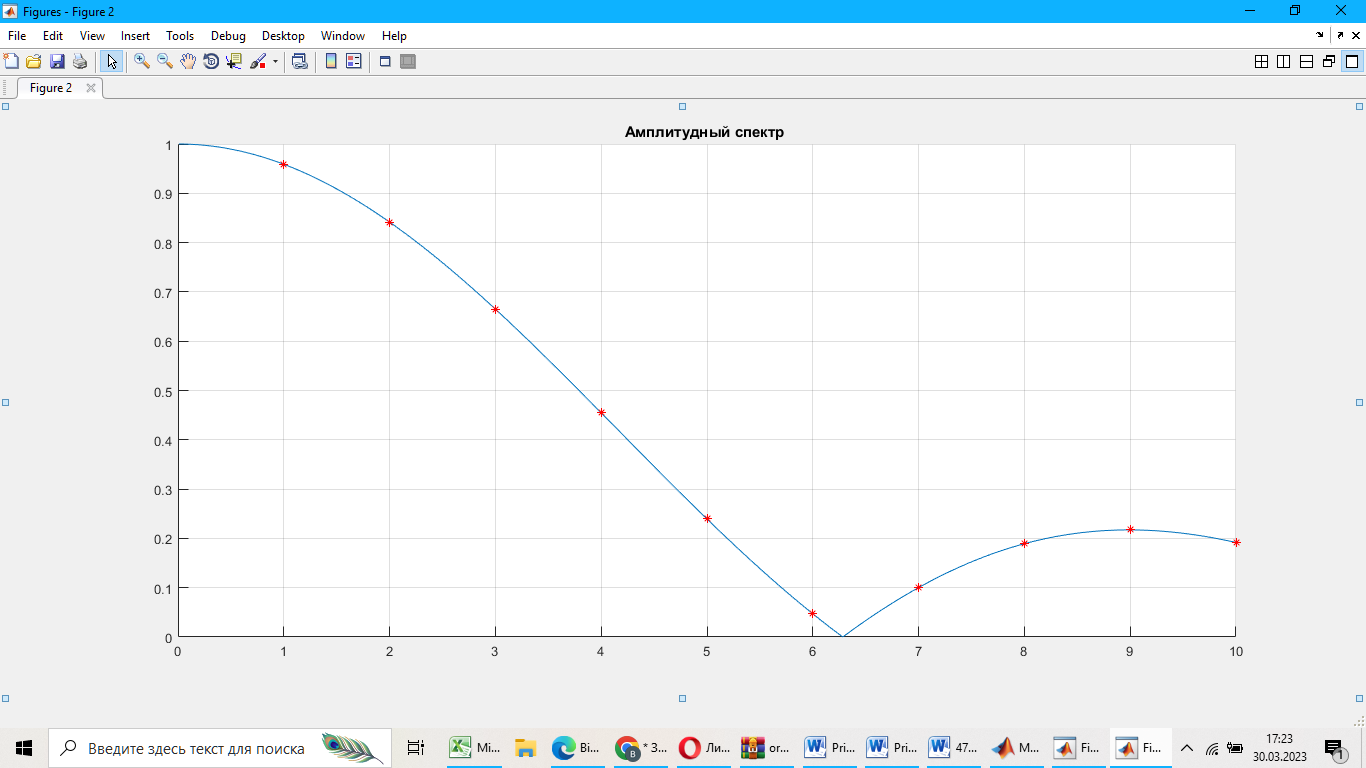
Рисунок 8
2. По п. 1-3 записать ряд Фурье и представить его в виде графика для трех гармоник (можно воспользоваться второй формой ряда Фурье).
Вторая тригонометрическая форма ряда Фурье:
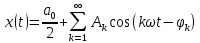
где
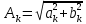
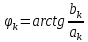
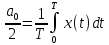
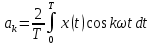
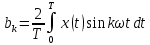
Тогда для прямоугольного сигнала, получим:
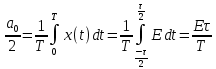
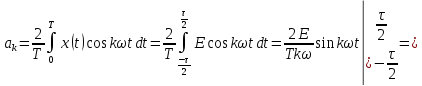
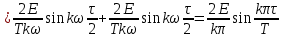
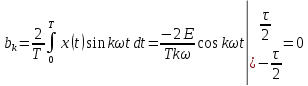
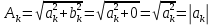
Тогда тригонометрический ряд Фурье будет равен:
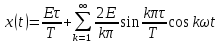
Для выполнения задания два использовалась следующая функция:
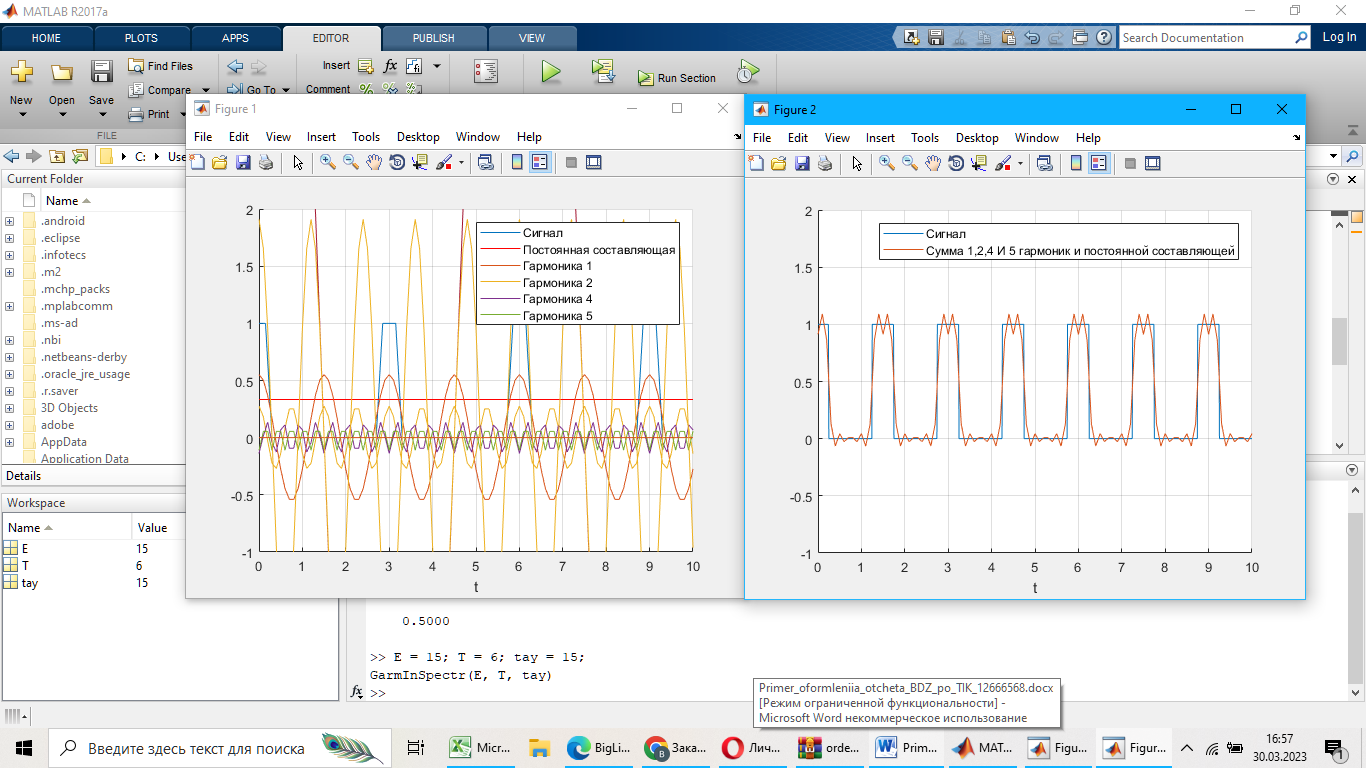
function F = GarmInSpectr(Am, T, tay)
figure(1)
hold on, grid on
t = (0:.01:20);
d = (0:T:20);
omega = Am.*pulstran(t, d, @rectpuls, tay);
plot(t, omega)
plot([0 10], [Am*tay/T Am*tay/T], 'r')
xlabel('t'), yl = ylabel('Am');
set(yl,'Units','Normalized','Position',[-1,2,0]);
axis([0 10 -1 2])
for k = 1:2
omega = 2*pi/T;
syms t
A = sum((2*E) / (k*pi) * sin(k*pi*tay/T) * cos(k*omega*t));
t = 0:0.1:10;
U = subs(A);
plot(t, U)
end
legend('Сигнал', 'Постоянная составляющая', 'Гармоника 1', 'Гармоника 2')
for k = 4:5
omega = 2*pi/T;
syms t
A = sum((2*Am) / (k*pi) * sin(k*pi*tay/T) * cos(k*omega*t));
t = 0:0.1:10;
U = subs(A);
plot(t, U)
end
legend('Сигнал', 'Постоянная составляющая', 'Гармоника 1', 'Гармоника 2', 'Гармоника 4', 'Гармоника 5')
figure(2)
hold on, grid on
t = (0:.01:10);
d = (0:T:10);
omega = Am.*pulstran(t, d, @rectpuls, tay);
plot(t, omega)
omega = 2*pi/T;
syms t
A = 0;
for k = 1:2
A = A + sum((2*Am) / (k*pi) * sin(k*pi*tay/T) * cos(k*omega*t));
end
for k = 4:5
A = A + sum((2*Am) / (k*pi) * sin(k*pi*tay/T) * cos(k*omega*t));
end
t = 0:0.1:10;
U = Am*tay/T + subs(A);
plot(t, U)
xlabel('t'), yl = ylabel('Am');
set(yl,'Units','Normalized','Position',[-1, 2,0]);
axis([0 10 -1 2])
legend('Сигнал', 'Сумма 1,2,4 И 5 гармоник и постоянной составляющей')
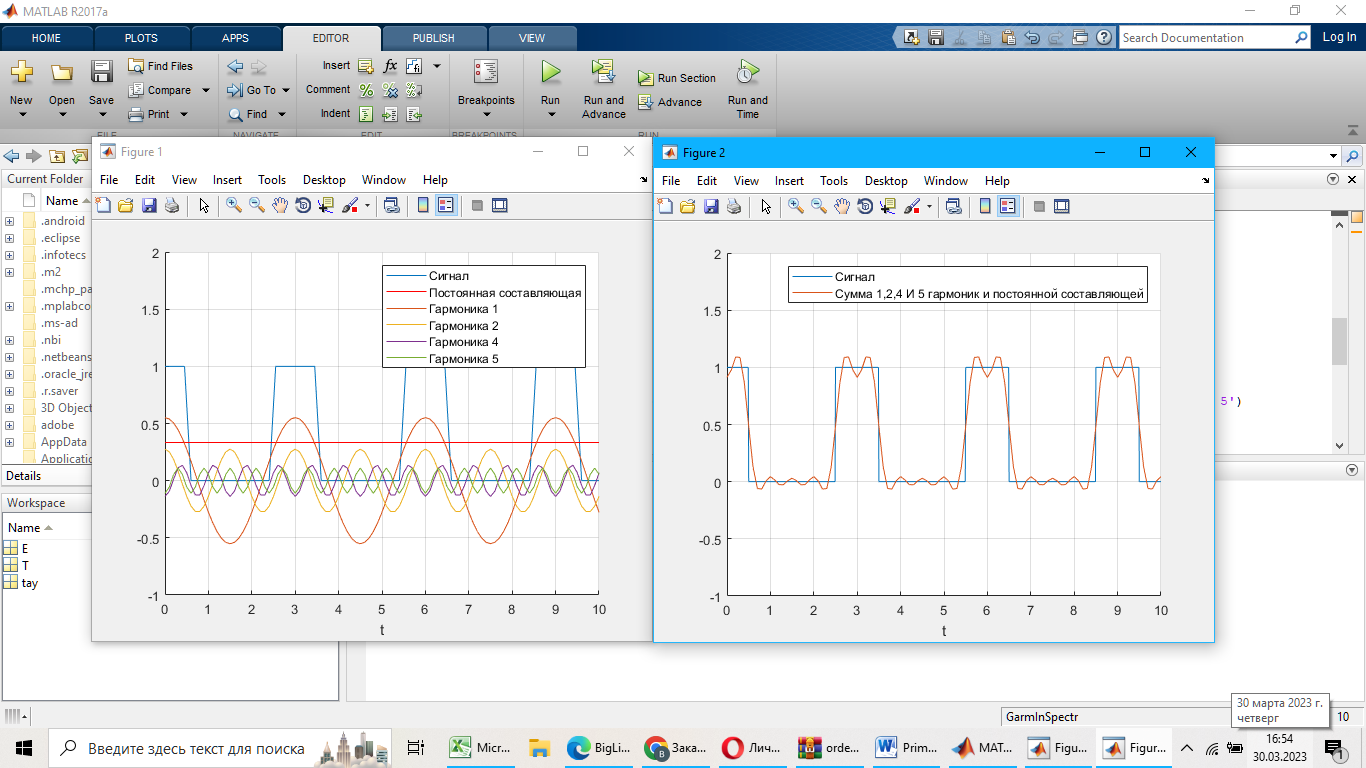
Гармоники первого сигнала:
E = 15; T = 3; tay = 15;
GarmInSpectr(E, T, tay)
Первая гармоника -
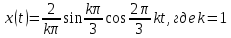
Вторая гармоника -
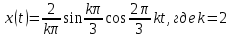
Третья гармоника -
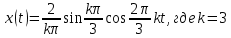
Постоянная составляющая –
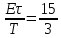
Гармоники второго сигнала:
E = 15; T = 1.5; tay = 0.5
GarmInSpectr(E, T, tay)
Первая гармоника -
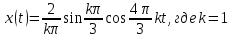
Вторая гармоника -
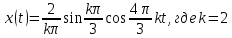
Третья гармоника -
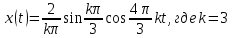
Постоянная составляющая –
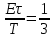
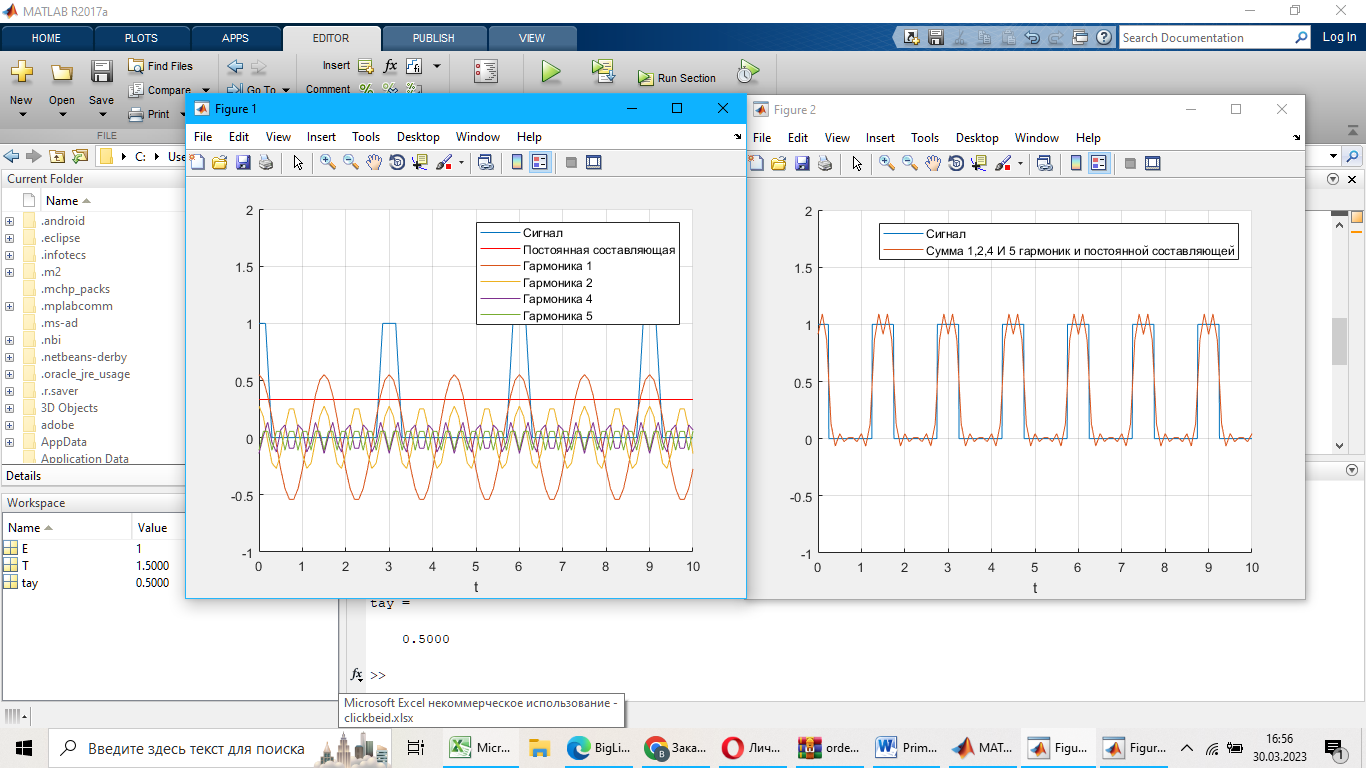
Гармоники третьего сигнала:
E = 15; T = 6; tay = 15;
GarmInSpectr(E, T, tay)
Первая гармоника -
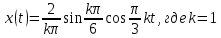
Вторая гармоника -
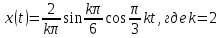
Третья гармоника -
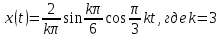
Постоянная составляющая –
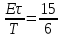
Вывод: Происходит изменение формы спектра при изменении при изменении параметров периодических импульсных сигналов: в случае увеличения расстояние между гармониками уменьшается, в случае уменьшения расстояние между гармониками увеличивается.