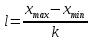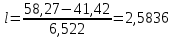Файл: Оптимизация буровых процессов и планирование эксперимента вариант4.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 27

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



Министерство науки и ВЫСШЕГО образования Российской Федерации

ФГБОУ ВО «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ имени Серго Орджоникидзе» (МГРИ)

______________________________________________________________________________________________________________

Дисциплина

«Оптимизация буровых процессов и планирование эксперимента»

Расчетная работа

Вариант №4

Выполнил: ст. группы ЗНД-17к

Глушко П.

Принял: доцент, к.т.н.

Фролова М.С.

Москва, 2022 г.

Содержание

1.Определение основных статистических оценок выборки

1.1 Среднее арифметическое выборки

1.2 Дисперсия

1.3 Среднеквадратическое отклонение

1.4 Отбраковка по критерию Шовене

1.5 Правило «трёх сигм»

1.6 Коэффициент вариации V

1.7 Доверительный интервал

1.8 Необходимое количество экспериментов

1.9 Проверка закона распределения СВ

1.10 Группировка данных

Вариант 4

49,13
46,55
49,07

57,92
57,55
48,57

51,28
50,2
46,41

49,78
53,49
47,58

48,38
41,42
50,36

53,04
54,4
57,36

50,57
47,03
51,97

50,49
50,68
45,2

53,13
47,41



44,31
51,77



48,28
48,63



56,06
53,89



47,99
46,29



49,38
54,42



49,7
50,83



49,61
51,74



54,73
58,27



42,48
52,63



53,53
48,77



53,13
42,89






Среднее арифметическое выборки

Это сумма всех значений выборки, деленная на её объем.

Формула:

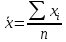
где





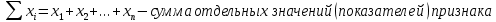
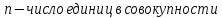
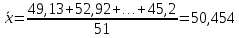
Дисперсия

Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.

Формула:



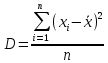
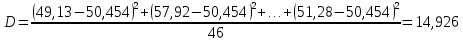
Среднеквадратическое отклонение

Это число, равное квадратному корню из дисперсии D.





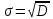
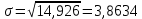
Отбраковка по критерию Шовене

При обработке статистического материала необходимо убедиться, что в выборке отсутствуют грубые ошибки. Грубые ошибки необходимо отбраковать с помощью критерия Шовене.

При отбраковке по критерию Шовене значение случайной величины должно находиться в интервале:



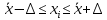
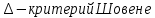
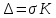где

, где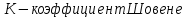

Коэффициент Шовене – табличный. Его значение при n=46 примерно равно 2,58.



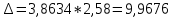
Интервал:





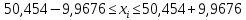
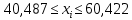
Все значения попадают в данный интервал.

Правило «трёх сигм»

Правило, утверждающее, что вероятность того, что случайная величина отклонится от своего математического ожидания более чем на три среднеквадратических отклонения, практически равна нулю.

Формула:





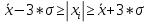
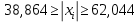
Все значения попадают в данный интервал.


Коэффициент вариации V

Для сравнения вариаций в любых совокупностях очень удобно пользоваться относительной величиной – коэффициентом вариации V, представляющим собой отношение среднего квадратического отклонения к средней арифметической:





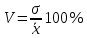
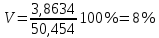
Доверительный интервал

Интервальная оценка с принятой вероятностью p или уровнем значимости 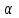определяет диапазон, в котором с определённой вероятностью будет находиться истинное значение средней величины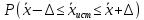



где Р – это доверительная вероятность, α – уровень значимости







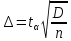
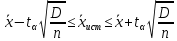
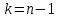
где k – степень свободы, 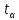- критерий Стьюдента, для n=46 равен 2,08 с α=0,05.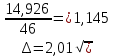





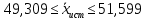
Необходимое количество экспериментов

Зависит от точности, которую нужно получить.









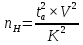
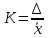
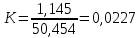
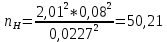
Проверка закона распределения СВ

Нормальный закон распределения выполняется в том случае, если соблюдается два условия:




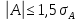
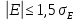
где A – показатель ассиметрии (характеризует симметричность левой и правой ветвей кривой), равный





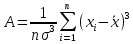
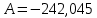
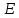
- показатель эксцесса (характеризует форму вершины кривой),





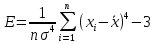
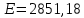
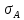- среднеквадратическое отклонение ассиметрии нормального закона.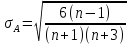





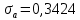
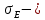среднеквадратическое отклонение эксцесса нормального распределения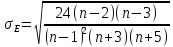





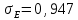
Оба условия выполнены, следовательно, выборка подчиняется нормальному закону распределения.

1.10 Группировка данных


Весь диапазон данных разбивают на классы.



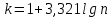
Где 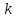- количество классов

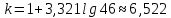. Результат округляем до целого.

Размер каждого класса находим по формуле:



Смотрите также файлы