Файл: Лабораторная работа 1 5 Бинарные деревья 5 Цель работы 5 Краткие теоретические сведения 5 Постановка задачи 6.docx

7. Интерфейс реализовать с помощью текстового меню.

6. Содержание отчета

1. Постановка задачи (общая и для конкретного варианта)

2. Анализ задачи

• 
  Определения функций для реализации поставленных задач
  
• 
  Определение функции main()
  

3. Блок-схема

4. Текст программы

5. Тесты

---

Лабораторная работа № 2

Введение в теорию графов. Алгоритмы Дейкстры и Флойда

2. 
   
   

   1. Цель работы:

Получить практические навыки работы с графами.

2. Краткие теоретические сведения

Реализовать обход графа, а также алгоритм Дейкстры или алгоритм Флойда. Вершина, с которой начать выполнение, указана в варианте.

Обходы графов: в глубину и в ширину

Обход графа – процедура однократного посещения всех вершин. Далее описаны 2 алгоритма обхода графа: в глубину и в ширину. Сначала будет разобран обход графа в глубину, затем обход графа в ширину.

Обход графа в глубину

По завершении обхода все вершины окажутся пройдёнными - обработанными. Если при обходе встречается вершина, которая уже была пройдена, то повторной обработки делать не нужно.

Рассмотрим следующий граф:



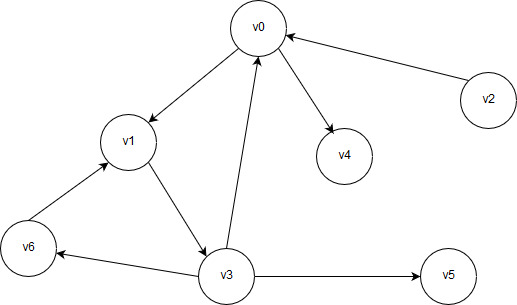
Рисунок 2.1 – Алгоритм обхода графа в глубину

Обход начинается с вершины v0. После обработки вершины v0 выполняется переход по одному из ребер к одной из соседних вершин. В данном примере существуют две возможности: перейти к вершине v1 или к вершине v4. Перейти от вершины v0 к вершине v2 или v3 невозможно, поскольку ребра, содержащие их, направлены в противоположную сторону. Итак, алгоритм обхода стоит перед выбором: перейти к вершине v1 или к вершине v4. Не имеет значения, как именно сделать этот выбор, - допустим, что выбрана вершина v1. После ее обработки рисунок будет выглядеть так:



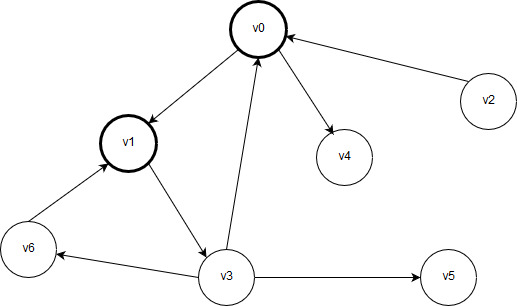
Рисунок 2.2 – Обработаны вершины v0 и v1

Затем алгоритм совершает переход к вершине, соседствующей с вершиной v1. Если соседняя вершина уже обработана, то алгоритм продвигается дальше, пропуская уже обработанные соседние вершины. В данном примере рассматривается только одна соседняя вершина v3 и обрабатывается. В данный момент обработанными являются три вершины, как показано ниже.



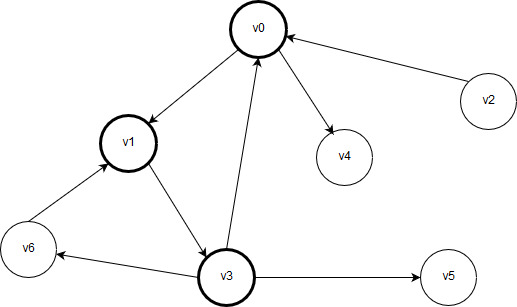
Рисунок 2.3 – Обработаны вершины v0, v1 и v3

Одной из соседних вершин по отношению к вершине v3 является вершина v0, однако она уже обработана. Таким образом, чтобы предотвратить зацикливание, переходить от вершины v3 в вершину v0 нельзя. Поэтому можно перейти к другому соседу: v5 или v6. Перейдем в вершину v5. После ее обработки на графе будут цветом отмечены вершины v0 и v1 как посещённые:

---

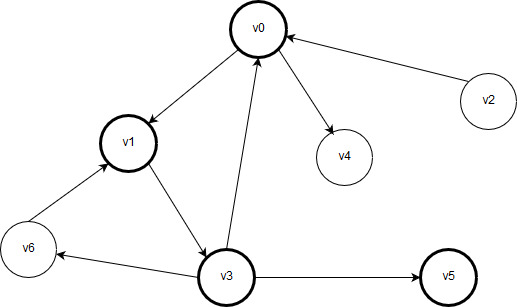
Рисунок 2.4 – Обработаны вершины v0, v1, v3 и v5

Поскольку у вершины v5 нет соседних вершин, дальнейший поиск в глубину невозможен. Далее, алгоритм возвращается назад и проверяет, нет ли у предыдущей вершины v3 других необработанных соседних вершин. У вершины v3 есть ещё необработанная соседняя вершина v6. Выполняется переход в вершину v6 и обработка вершины v6. После обработки вершины v6 рисунок имеет следующий вид:



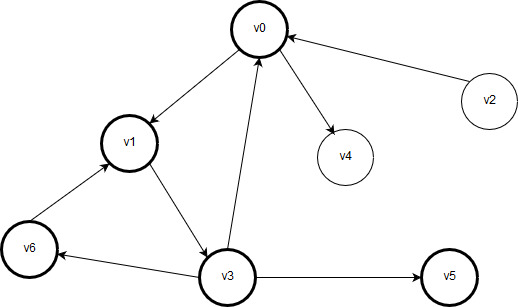
Рисунок 2.5 – Вершина v6 обработана после возврата к вершине v3

У вершины v6 есть соседняя вершина – v1, однако она уже обработана. Таким образом, у вершины v6 нет обработанных соседних вершин, поэтому обход возвращается назад – в вершину v3, чтобы проверить, остались ли у нее другие необработанные соседи. У вершины v3 больше нет необработанных соседей. Значит, алгоритм возвращается к предыдущей вершине v1, чтобы проверить, есть ли у нее непомеченные соседние вершины. У вершины v1 нет необработанных соседних вершин, поэтому выполняется возврат в вершину v0 для проверки, есть ли у вершины v0 необработанные соседи. Такой сосед есть – это вершина v4, поэтому алгоритм переходит в нее. После перехода граф выглядит так:



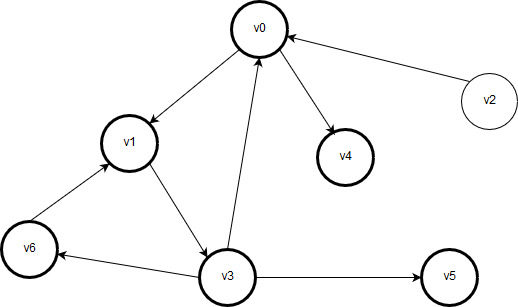
Рисунок 2.6 – Вершина v4 обработана

У вершины v4 соседних вершин нет, поэтому происходит возврат в вершину v0. У вершины v0 больше нет необработанных соседних вершин. Поскольку вершина v0 была отправной точкой нашего обхода, дальнейшее перемещение по графу невозможно (из вершины v0 в вершину v2 попасть невозможно). Обход графа завершен.

Во время обхода графа в глубину обрабатываются лишь те вершины, которые достижимы из начальной вершины графа. Существует еще одно важное свойство обхода графа в глубину: из начальной вершины осуществляется переход в соседнюю вершину, оттуда – в соседнюю к соседней и так далее – при этом обход графа осуществляется настолько глубоко, насколько это возможно, и только потом выполняется возврат в исходную вершину. Таким образом, алгоритм обхода графа в глубину работает рекурсивно.

Обход в ширину

Этот алгоритм использует очередь для отслеживания необработанных соседних вершин. Этот алгоритм обхода графа применяется для поиска компонент связности в графе, а также, как и алгоритм обхода в глубину, применяется при прохождении лабиринтов. Поиск начинается с начальной вершины, которая обрабатывается, маркируется и помещается в очередь. Возьмем для примера граф, рассмотренный на рисунке 2.1.

---

Предположим, что начальной является вершина v0. Тогда вершина является первой вершиной, подлежащей обработке, маркировке цветом и сохранению в очереди.




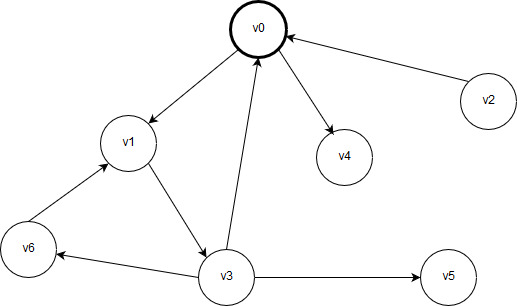
Рисунок 2.7 – Вершина v0 промаркирована и занесена в очередь

На данный момент в голове очереди находится начальная вершина v0.

После того, как начальная вершина обработана, промаркирована и помещена в очередь, начинается выполнение основной части алгоритма обхода графа в ширину. Основой алгоритма является циклический процесс, в котором обработанная вершина удаляется из очереди, а в очередь помещаются соседствующие с обработанной вершины. Таким образом, тело цикла состоит из двух основных шагов:

- Удалить вершину v из головы очереди

- Для каждой непомеченной вершины u, соседней по отношению к вершине v, обработать вершину u, маркировать ее и поместить в очередь (вершина u может иметь соседние необработанные вершины).

Эти действия выполняются до тех пор, пока очередь не станет пустой.

Рассмотрим работу алгоритма на примере, когда вершина v0 находится в голове очереди (рисунок 2.7). Вершина v0 удаляется из очереди и отмечается, что у нее остались необработанными две соседние вершины – v1 и v4. Каждая из них обрабатывается, маркируется и помещается в очередь. Допустим, сначала в очередь поставлена вершина v1, а затем вершина v4 (очередность может быть любой, вершина v4 может быть поставлена первой, а вершина v1 за ней – алгоритм будет работать корректно в любом случае). После того, как вершины v1 и v4 были поставлены в очередь, граф выглядит следующим образом:





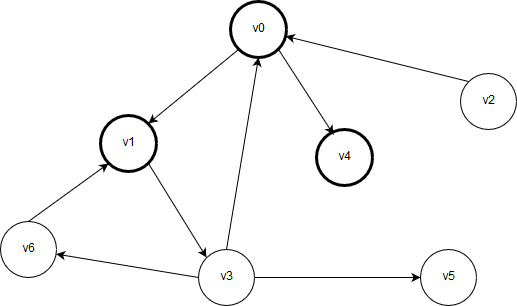
Рисунок 2.8 – Промаркированы вершины v0, v1, v4, в очереди находятся вершины v1 и v4

Поскольку очередь не пуста, два шага выполняются снова: первый элемент (вершина v1) удаляется, обрабатывается, все необработанные соседние вершины маркируются и помещаются в очередь. Единственным неотмеченным соседом вершины v1 является вершина v3, поэтому после обработки, маркировки и постановки в очередь вершины v3 граф выглядит так:

---

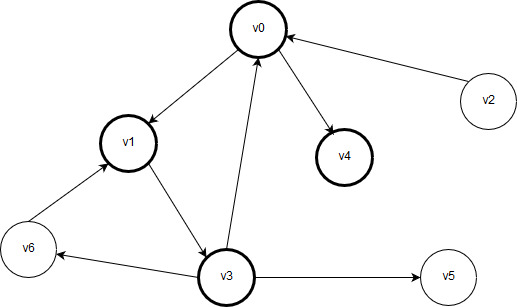
Рисунок 2.9 – Промаркированы вершины v0, v1, v4, v3, в очереди находятся вершины v3 и v4

Далее из головы очереди удаляется вершина v4. Поскольку у нее нет соседних вершин, никакие вершины больше не обрабатываются и не становятся в очередь, при этом граф выглядит так:





Рисунок 2.10 - Промаркированы вершины v0, v1, v4, v3, в очереди находится только вершина v3

Следующей из очереди удаляется вершина v3. У нее есть две непомеченные соседние вершины (вершины v5 и v6), которые обрабатываются, маркируются и помещаются в очередь. Граф выглядит следующим образом:





Рисунок 2.11 – Промаркированы вершины v0, v1, v4, v3, v5, v6, в очереди находятся вершины v5 и v6

Вершина v0 не обрабатывается повторно, так как она уже помечена.

Результат обхода графа в глубину и в ширину одинаков – отличается порядок обработки. Вершины v0, v1, v3, v4, v5 и v6 обработаны, поскольку все они достижимы из начальной точки (вершины 0). Вершина v2 не обрабатывается, поскольку не существует пути из вершины v0 в вершину v2. При обходе графа в ширину вершины обрабатываются в следующем порядке: сначала вершина v0, потом v1 и v4, затем обрабатываются их соседи (вершина v3) и так далее. При обходе графа в глубину сначала обрабатываются вершины v0, v1, v3 и v5.

Алгоритм Дейкстры

Рассмотрим следующий граф:


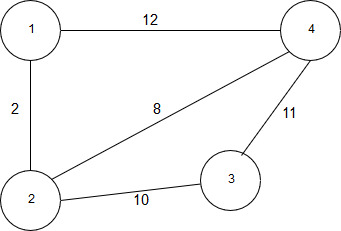
Рисунок 2.12 - Поиск кратчайшего пути по алгоритму Дейкстры

Пусть требуется найти кратчайшие расстояния от вершины 1 до всех остальных вершин графа. Длина пути между вершинами, называемая весом, обозначена над ребрами графа.

Алгоритм предполагает, что все вершины графа должны быть размечены, метка означает длину кратчайшего пути в эту вершину из заданной вершины 1. Следовательно, метка заданной вершины 1 устанавливается равной 0. Метки остальных вершин устанавливаются равными недостижимо большому числу, что отражает то, что расстояния от вершины 1 до других вершин пока не известны. В начале алгоритма все вершины графа помечаются как необработанные.

---