Файл: Лабораторная работа 1 5 Бинарные деревья 5 Цель работы 5 Краткие теоретические сведения 5 Постановка задачи 6.docx

Варианты заданий

№ варианта		Задание
1		Реализовать граф, а также алгоритм обхода графа в глубину (выполнение с вершины 1).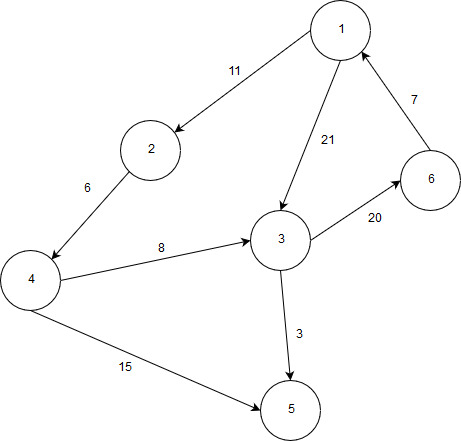
2	Реализовать граф, а также алгоритм Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 6.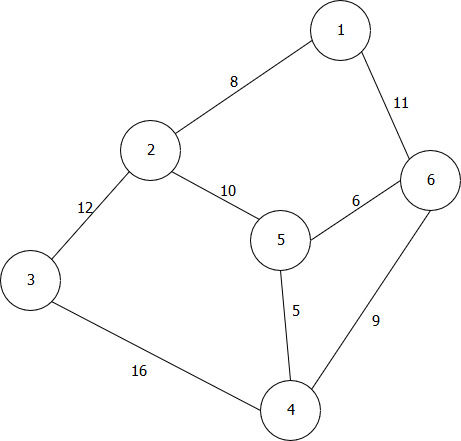
3	Реализовать граф, а также алгоритм обхода графа в ширину (выполнение с вершины 4).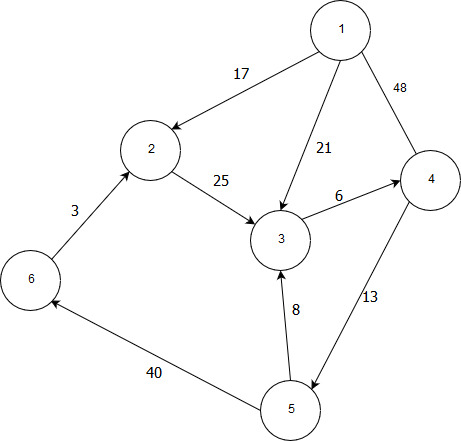
4	Реализовать граф, а также алгоритм Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 2.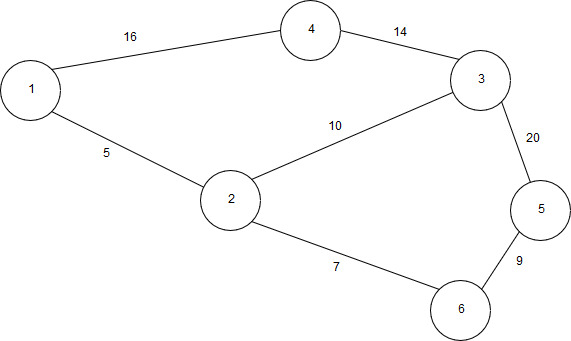

5	Реализовать граф, а также алгоритм Флойда, построив все необходимые матрицы. Выполнение начать с вершины 1.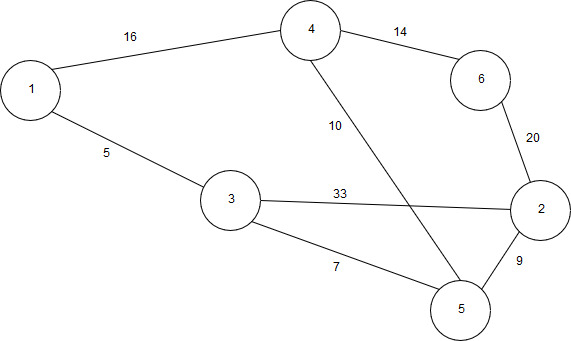
6	Реализовать граф, а также алгоритм Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 6.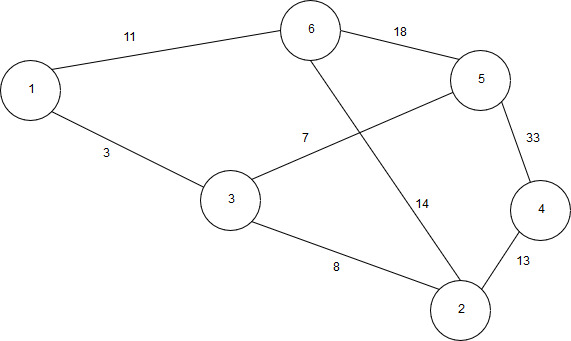
7	Реализовать граф, а также алгоритм обхода графа в глубину (выполнение с вершины 1).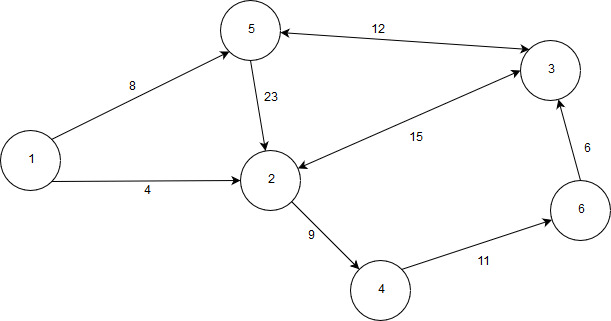

---

8	Реализовать граф, а также алгоритм Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 4.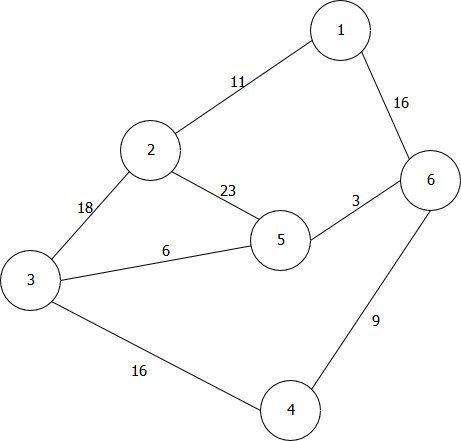
9	Реализовать граф, а также алгоритм обхода графа в ширину (выполнение с вершины 3).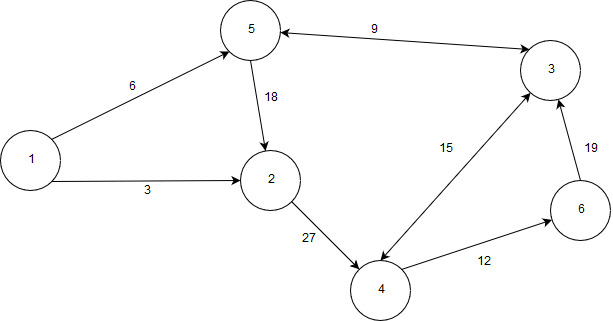
10	Реализовать граф, а также алгоритм Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 6.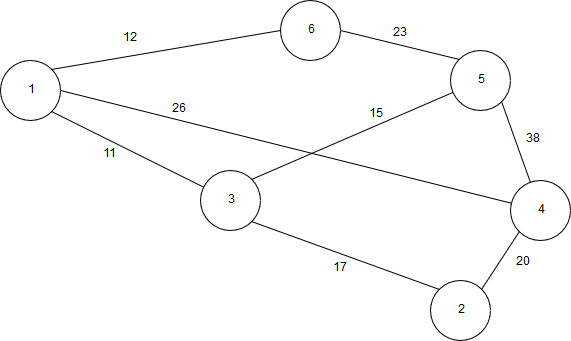

11	Реализовать граф, а также алгоритм Флойда, построив все необходимые матрицы. Выполнение начать с вершины 7.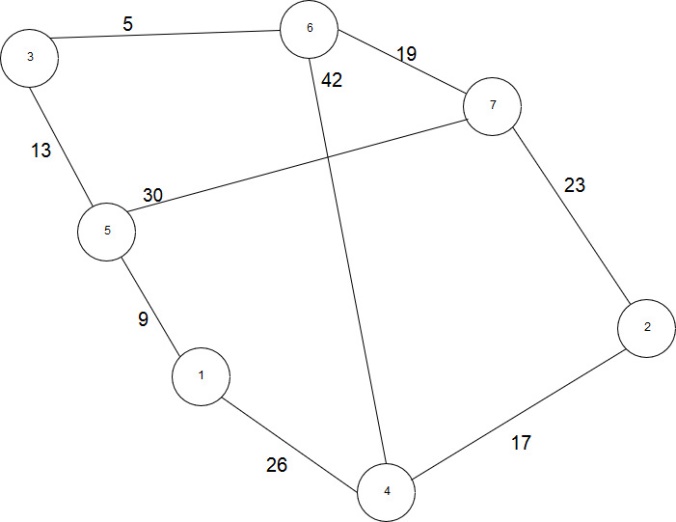
12	Реализовать граф, а также алгоритм Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 6.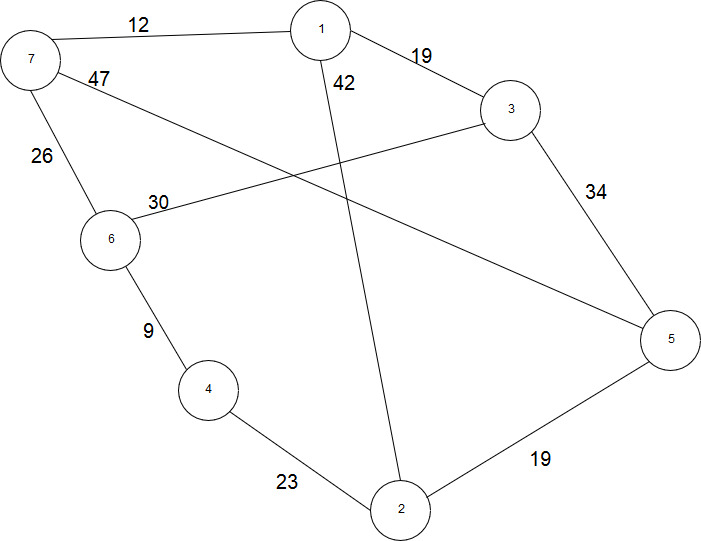
13	Реализовать граф, а также алгоритм Флойда, построив все необходимые матрицы. Выполнение начать с вершины 1.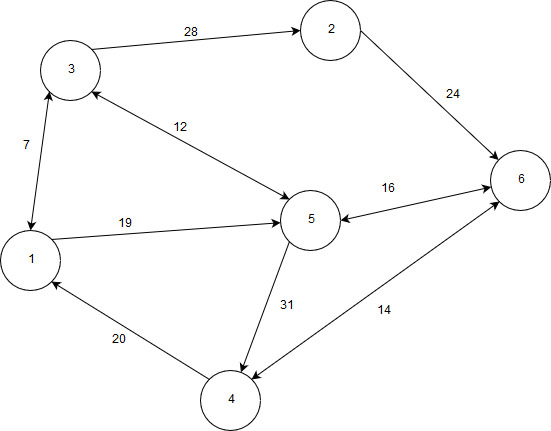

14	Реализовать граф, а также алгоритм Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 3.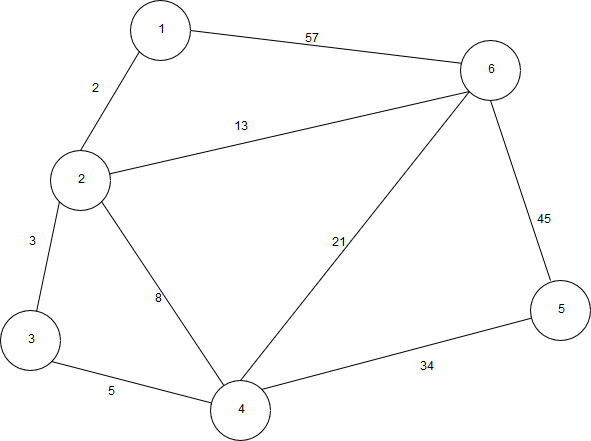
15	Реализовать граф, а также Флойда, построив все необходимые матрицы. Выполнение начать с вершины 1.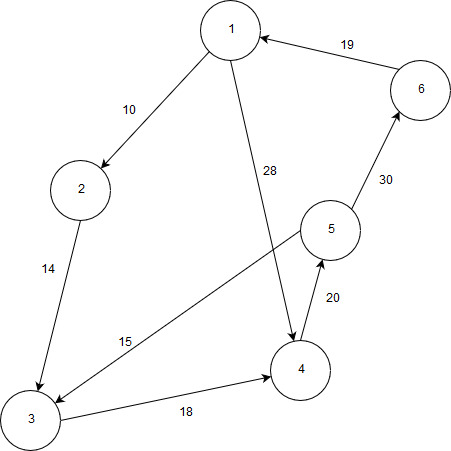
16	Реализовать граф, а также Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 2.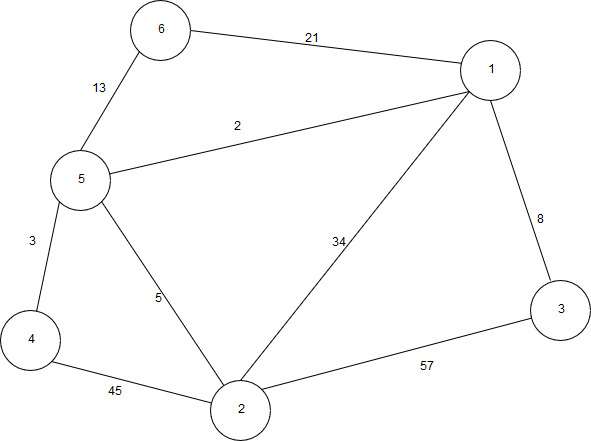

---

17	Реализовать граф, а также Флойда, построив все необходимые матрицы. Выполнение начать с вершины 3.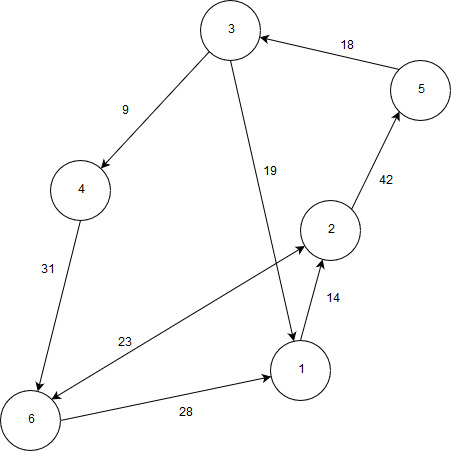
18	Реализовать граф, а также Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 3.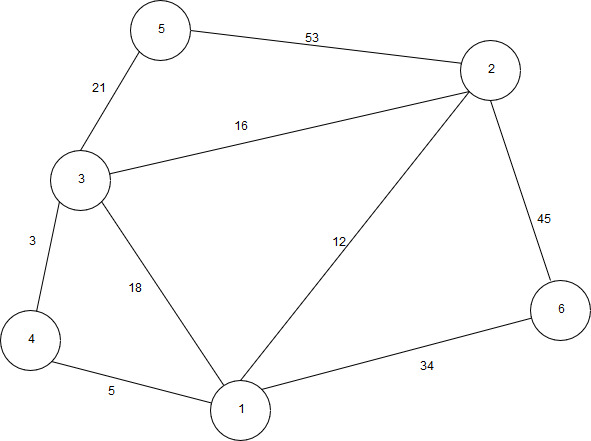
19	Реализовать граф, а также Флойда, построив все необходимые матрицы. Выполнение начать с вершины 5.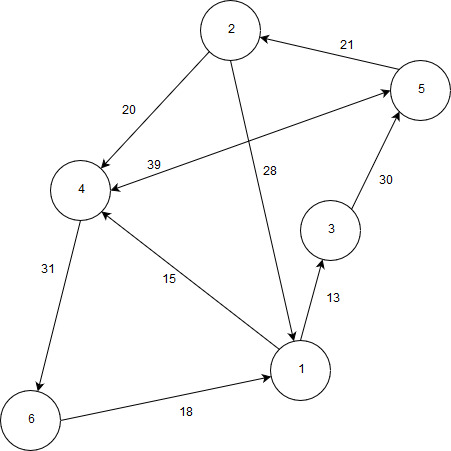

20	Реализовать граф, а также Флойда, построив все необходимые матрицы. Выполнение начать с вершины 3.
21	Реализовать граф, а также Дейкстры, выполнив все необходимые действия. Выполнение начать с вершины 3.
22	Реализовать граф, а также Флойда, построив все необходимые матрицы. Выполнение начать с вершины 5.

4. Содержание отчета

1. Постановка задачи (общая и для конкретного варианта)

2. Анализ задачи

• 
  Определения функций для реализации поставленных задач
  
• 
  Определение функции main()
  

3. Блок-схемы основных функций

4. Текст программы

5. Тесты

---

Лабораторная работа № 3

Динамическое программирование. Задача коммивояжера

3. 
   
   

   1. Цель работы:

Изучить алгоритм решения задачи коммивояжера и научиться использовать его в графе.

2. Краткие теоретические сведения

Практическое применение задачи коммивояжера

Применение задачи коммивояжера на практике довольно обширно, ее можно использовать для поиска кратчайшего пути на гастролях эстрадной группы или обеспечения наименьшего времени выполнения производственного цикла и других решения других оптимизационных задач.



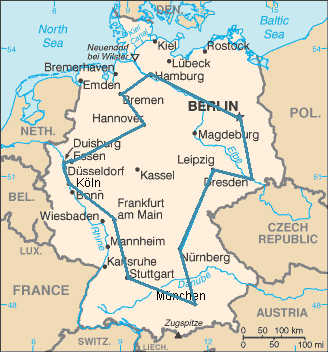
Рисунок 3.1 – Оптимальный маршрут коммивояжёра через 15 крупнейших городов Германии. Указанный маршрут является самым коротким из всех возможных 43589145600 вариантов

3. Постановка задачи

Имеется N городов. Выезжая из исходного города А1, коммивояжер должен побывать во всех городах по одному разу и вернуться в город А1. Задача заключается в определении последовательности объезда городов, при которой коммивояжеру требуется минимизировать некоторый критерий эффективности: стоимость проезда, время пути, суммарное расстояние.

Для расчета затрат существует матрица условий, содержащая затраты на переход из каждого города в каждый, при этом считается, что можно перейти из любого города в любой, кроме того же самого. Целью решения является нахождения маршрута, удовлетворяющего всем условиям и при этом имеющего минимальную сумму затрат.

Анализ задачи коммивояжера

Для решения задачи коммивояжера составляется матрица условий, которая содержит расстояния между городами. Считается, что можно перейти из любого города в любой, кроме того же самого. Так как пути из города А в город А по условию нет, обозначим его «нн».


Рисунок 3.2 – Матрица условий

После построения изначальной матрицы условий проводим редукцию строк и столбцов.

Редукция строк: находим минимальное расстояние в строке,

---

вычитаем его из всех расстояний в строке, кроме «нн».



Рисунок 3.3 – Редукция строк (минимальные элементы подчеркнуты)

Редукция столбцов: находим минимальное расстояние в столбце, вычитаем его из всех расстояний в столбце, кроме «нн».



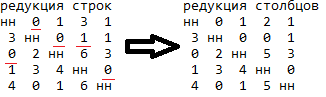
Рисунок 3.4 – Редукция столбцов (мин. элементы подчеркнуты)

Оценка нулей: каждый 0 в таблице оцениваем: считаем сумму минимального элемента в строке и в столбце и запоминаем результат.



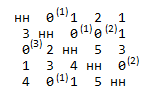
Рисунок 3.5 – Оценка нулей

Чистка карты: выбираем 0 с наибольшей оценкой, если таких несколько, выбираем любой, вычеркиваем строку и столбец, в котором находится этот 0 (вычеркивание — замена элементов строки и столбца на «нн»).



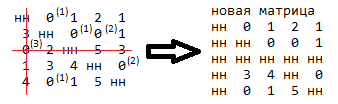
Рисунок 3.6 – Чистка карты

Координаты вычеркнутого столбца и строки запоминаем, назовем их ребрами. Повторяем редукцию столбцов, строк и чистку карты, пока последний переход не станет очевидным (сведем матрицу к размерам 2х2).



Рисунок 3.7 – Сведение исходной матрицы к матрице 2х2



Рисунок 3.8 – Сведение исходной матрицы к матрице 2х2

Полученные ребра выстраиваем в последовательность и получаем наименьший путь, из исходной матрицы берем расстояния, двигаясь по проложенному пути, получаем оптимальное расстояние всего пути.

Результат решения задачи коммивояжера:

3->1->2->4->5->3

весь путь:

18

4. Варианты заданий

№ матрицы	Матрица условий
1	нн 21 27 41 20 нн 2 56 14 38 нн 1 5 24 46 нн

---