Файл: Лабораторная работа 1 5 Бинарные деревья 5 Цель работы 5 Краткие теоретические сведения 5 Постановка задачи 6.docx

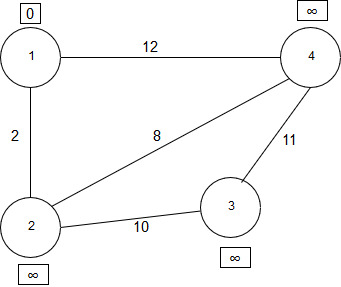
Рисунок 2.13 - Вершинам графа поставлены соответствующие метки

Первый шаг алгоритма:

Минимальную метку, равную нулю, имеет вершина 1. Её соседями являются вершины 2 и 4. Алгоритм обходит соседей вершины по очереди. Первый сосед вершины 1 – вершина 2, так как длина пути до неё минимальна. Длина пути в неё через вершину 1
равна сумме кратчайшего расстояния до вершины 1 (значению её метки) и длины ребра, идущего из вершины 1 в вершину 2, то есть

0 + 2 = 2.

Из двух меток – текущей, равной бесконечности, и рассчитанной, равной 2, выбирается наименьшая. Поэтому новая метка 2-ой вершины будет равна 2, что показано на рисунке ниже.


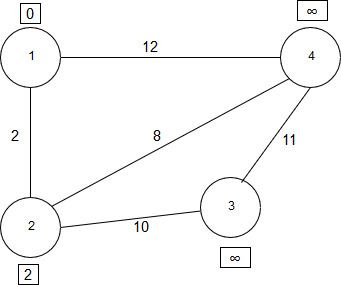
Рисунок 2.14 – Метка у вершины 2 изменена

Аналогично находятся длины путей для всех других соседей - вершины 4. От вершины 1 до вершины 4 кратчайшим будет расстояние в 12 единиц:

0 + 12 = 12.

Все соседи вершины 1 проверены. На данный момент все вершины, в которые можно попасть из вершины 1 напрямую, проверены. Вершина 1 отмечается как обработанная. Для графа, изображенного на рисунке ниже, таким расстоянием будет путь, равный двум единицам.



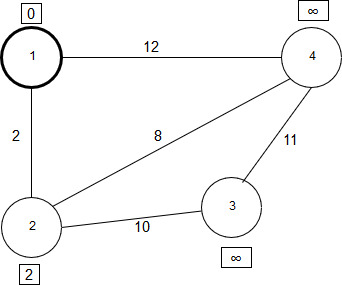
Рисунок 21.15 – Вершина 1 обработана

Второй шаг алгоритма:

Снова находится «ближайшая» из необработанных вершин. Это вершина 2 с меткой 2.

Согласно алгоритму, снова предпринимается попытка уменьшить метки соседей выбранной вершины, используя для перехода в них 2-ю вершину в качестве промежуточной. Соседями вершины 2 являются вершины 1 и 3. Вершина 1 уже обработана. Следующий сосед вершины 2 – вершина 4, так как до нее расстояние от вершины 2 будет меньше, чем до вершины 3. Длина пути от вершины 1 до вершины 4 составит 10 единиц:

2+8=10.

Полученное расстояние меньше 12, поэтому у вершины 4 ставится метка 10. Далее рассматривается вершина 3. Расстояние до нее от вершины 1 через вершину 2 составит 12 единиц:

2+10=12.

Полученное значение меньше бесконечности, поэтому метка вершины 3 меняется с бесконечности на 12. Вершина 2 отмечается как посещенная, что показано на рисунке ниже.

---

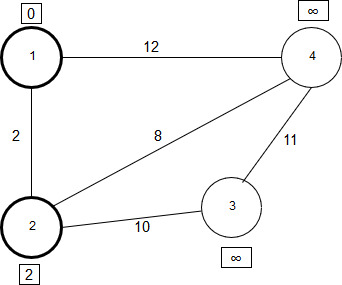
Рисунок 2.16 - Вершина 2 обработана

Третий шаг:

Обрабатывается вершина 4, после ее обработки ничего не меняется, поскольку если идти в вершину 3 через вершину 4 (предварительно посетив вершину 2, так как кратчайший путь в вершину 4 лежит через вершину 2), то расстояние составит

10+11=21 (ед).

Полученное расстояние больше, чем текущая метка вершины 3, поэтому метка вершины 3 меняться не будет. Граф на этом шаге выглядит так:


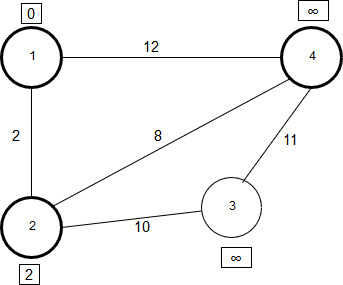
Рисунок 2.17 - Вершина 4 обработана

На четвертом шаге алгоритма обрабатывается вершина 3. После её обработки также ни одна метка не изменится, поскольку все остальные вершины уже обработаны, следовательно кратчайшие расстояния до них пересмотру не подлежат. На третьем шаге было выяснено, что от вершины 4 до вершины 3 путь более выгодным не является, поэтому метка вершины 3 осталась прежней. На текущем (и последнем) шаге алгоритма вершина 3 отмечается как посещенная. Граф выглядит так:



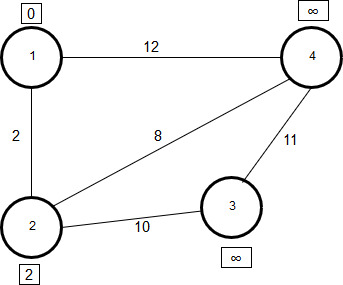
Рисунок 2.16 - Вершина 3 обработана
Таким образом, кратчайший путь от вершины 1 до вершины 3 проходит через вершины 1-2-3 и имеет минимальное расстояние, равное 12 единицам.

Алгоритм Флойда

Данный алгоритм ищет кратчайшие пути от каждой из вершин графа до всех остальных.

Рассмотрим граф:



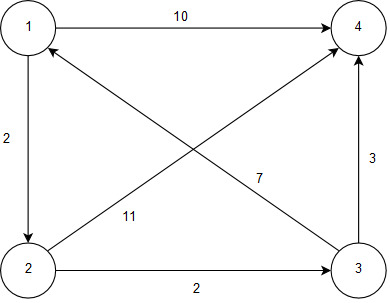
Рисунок 2.17 – Алгоритм Флойда

Метод предполагает создание двух матриц: матрицы кратчайших расстояний – первой матрицы и матрицы для построения пути – второй матрицы.

В начале алгоритма первая матрица изначально совпадает с матрицей смежности:

№ вершины	1	2	3	4
1	0	2	10000	10
2	10000	0	2	11
3	7	10000	0	3
4	10000	10000	10000	0

---

Рисунок 2.18 – Первая матрица в начальном состоянии

В первой матрице значения 10000 взяты условно, на самом деле они отражают очень большое число, которое значительно больше веса любого из ребер данного графа. В дальнейшем при описании алгоритма вместо 10000 будет употребляться понятие «бесконечность». Расстояние из вершины до самой себя равно 0, в остальных полях матрицы все значения обозначают расстояния, которые необходимо преодолеть от одной вершины к другой, причем расстояния эти самые короткие. Во время работы алгоритма некоторые из значений, хранящихся в первой матрице, будут меняться, уменьшаясь.

Вторая матрица предназначена для построения кратчайшего пути:
Вторая матрица:

№ вершины	1	2	3	4
1	0	2	0	4
2	0	0	3	4
3	1	0	0	4
4	0	0	0	0

Рисунок 2.19 – Вторая матрица в начальном состоянии

. Поясним, какие значения там хранятся: во второй матрице хранятся номера вершин, в которые надо пройти, чтобы попасть в желаемую. То есть, поле [1,2] означает: чтобы попасть из вершины 1 в вершину 2, необходимо пройти через вершину, которая хранится в поле [1,2], а именно через вершину 2. Так как путь из любой вершины до самой себя равен 0, то на главной диагонали матрицы стоят нули. Также нули стоят там, куда невозможно прийти на данный момент (так как из вершины 1 в вершину 3 попасть невозможно, то в поле матрицы [1,3] стоит 0).

Алгоритм Флойда работает следующим образом:

Пусть начальной вершиной является вершина 1. Алгоритм определяет, в какую вершину можно попасть из начальной вершины, используя только одну промежуточную вершину. Можно попасть, например, в вершину 3 через вершину 2; а также в вершину 4 через вершину 2. Кроме того, можно остаться в вершине 1.

---

Итак, определено, что, используя одну промежуточную вершину, можно попасть в вершины 3 и 4.

Рассчитаем в условных единицах затраты на преодоление каждого пути: чтобы попасть в вершину 3 из вершины 1 через вершину 2 потребуется 4 условных единицы. Чтобы попасть в вершину 4 через вершину 2, потребуется 13 условных единиц. Алгоритм сравнивает полученные значения с теми значениями, которые на данный момент находятся в первой матрице:

чтобы пройти из вершины 1 в вершину 3 потребуется бесконечно много условных единиц, то есть на данный момент добраться из вершины 1 в вершину 3 невозможно. В то же время найден путь, в котором придется затратить только 4 условных единицы для того, чтобы попасть из вершины 1 в вершину 3. Затраты в 4 условные единицы на преодоление пути меньше, чем бесконечное значение затрат, поэтому в первой матрице в поле [1,3] записывается вместо бесконечно большого значения значение 4. Затем длина пути из вершины 1 в вершину 4 через вершину 2 с затратами 13 условных единиц сравнивается со значением, хранящимся в поле [1,4] первой матрицы. Затраты в 13 условных единиц больше, чем в 10 условных единиц, то есть рассмотренный путь не является более выгодным. Следовательно, во второй матрице в поле [1,3] записывается 2, поскольку чтобы попасть из вершины 1 в вершину 3, нужно сначала пройти в вершину 2.

На этом этапе матрицы выглядят так:
Первая матрица:

№ вершины	1	2	3	4
1	0	2	4	10
2	10000	0	2	11
3	7	10000	0	3
4	10000	10000	10000	0

Рисунок 2.20 – От вершины 1 найдено более короткое расстояние в вершину 3

Вторая матрица:

№ вершины	1	2	3	4
1	0	2	2	4
2	0	0	3	4
3	1	0	0	4
4	0	0	0	0

---

Рисунок 2.21 – Во вторую матрицу записана в качестве промежуточной вершины вершина 2 (путь из вершины 1 в вершину 3)

Далее, алгоритм ищет, в какие вершины можно попасть из вершины 1, используя две промежуточные вершины. Такой является вершина 4 (путь через вершины 2 и 3). Затраты на преодоление этого пути составляют

2+2+3=7.

Больше таким способом попасть никуда нельзя.

Затраты в 7 условных единиц меньше, чем 10 условных единиц, поэтому в первую матрицу в поле [1,4] записывается значение 7. Во вторую матрицу в поле [1,4] записывается значение 2, поскольку, чтобы по кратчайшему пути попасть из вершины 1 в вершину 4, нужно сначала пройти вершину 2.

На этом этапе матрицы выглядят так:
Первая матрица:

№ вершины	1	2	3	4
1	0	2	4	7
2	10000	0	2	11
3	7	10000	0	3
4	10000	10000	10000	0

Рисунок 2.22 – В первую матрицу занесено значение 7 – затраты на преодоление пути из вершины 1 в вершину 4

Вторая матрица:

№ вершины	1	2	3	4
1	0	2	2	2
2	0	0	3	4
3	1	0	0	4
4	0	0	0	0

---